Hemmes mathematische Rätsel: Spezialbögen
Der 1932 geborene amerikanische Mathematiker John E. Wetzel hat viele wunderbare und knifflige mathematische Knobeleien erfunden. Von allen seinen eigenen Rätseln hält er das Problem der Spezialbögen für das schönste. Man findet es in dem 1994 erschienenem Buch »In Eves' Circles« von Joby Milo Anthony und Howard Whitley Eves.
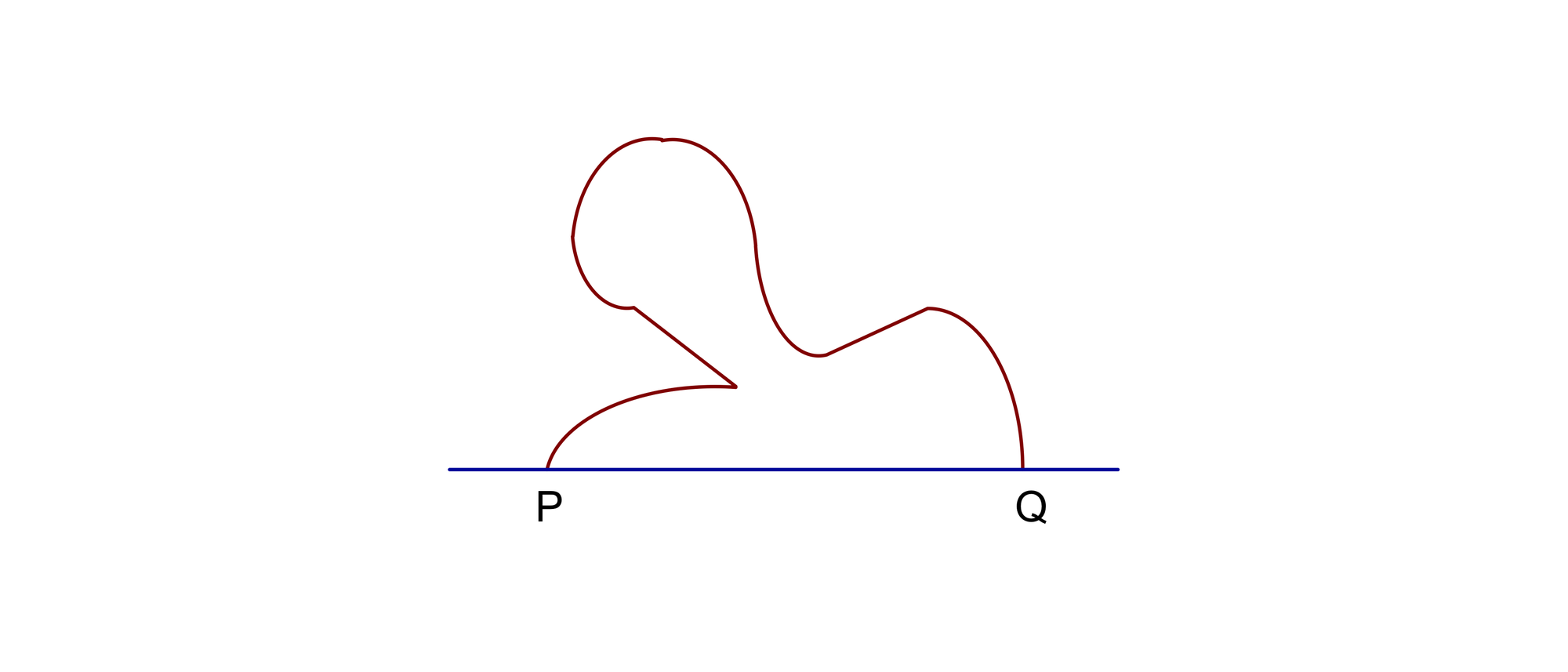
Ein Spezialbogen ist eine ebene Kurve der Länge 1 mit den beiden Endpunkten P und Q. Ein Spezialbogen darf beliebig kompliziert geformt sein und aus geraden und gekrümmten Abschnitten bestehen, und er darf sich auch selbst schneiden. Er muss allerdings vollständig auf einer Seite der Geraden liegen, die durch seine beiden Endpunkte läuft. Entwerfen Sie einen möglichst einfachen Spezialbogen, den man nicht vollständig mit einem rechtwinklig gleichschenkligen Dreieck, dessen Hypotenuse die Länge 1 hat, abdecken kann.
Zunächst einmal wird das kleinste rechtwinklige, gleichschenklige Dreieck ABC konstruiert, das den kompletten Spezialbogen umschlingt und dessen Hypotenuse auf die Gerade fällt, die durch die Endpunkte P und Q läuft. Die Katheten berühren den Bogen in den Punkten R und S.
Nun wird der Bogen an den beiden Katheten gespiegelt. Dabei wird P zu P' und Q zu Q'. Der Originalbogen hat die gleiche Länge wie die drei Bogenstücke P'R, RS und SQ' zusammen. Da die beiden spitzen Winkel des Dreiecks ABC je 45 Grad groß sind, liegen die Strecken AP' und BQ' parallel zueinander. Darum können die drei Bogenstücke zusammen aber höchstens so lang sein wie die Hypotenuse AB. Folglich gibt es keinen Spezialbogen, den man nicht vollständig mit einem rechtwinklig gleichschenkligen Dreieck, dessen Hypotenuse die Länge 1 hat, abdecken kann.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.