Hemmes mathematische Rätsel: Spielzeug auf der Waage

Sam Loyd, Amerikas berühmtester Rätsel- und Spieleerfinder, wurde 1841 in Philadelphia geboren. Ab 1890 schrieb er für etliche Zeitschriften regelmäßige Rätselkolumnen. Loyd starb 1911 in New York. Vier Jahre nach seinem Tod gab sein Sohn die Rätsel seines Vaters in einem Buch mit dem Titel »Sam Loyd's Cyclopedia of 5000 Puzzles, Tricks and Conundrums with Answers« heraus. Aus diesem Klassiker des Denksports stammt das folgende Problem.
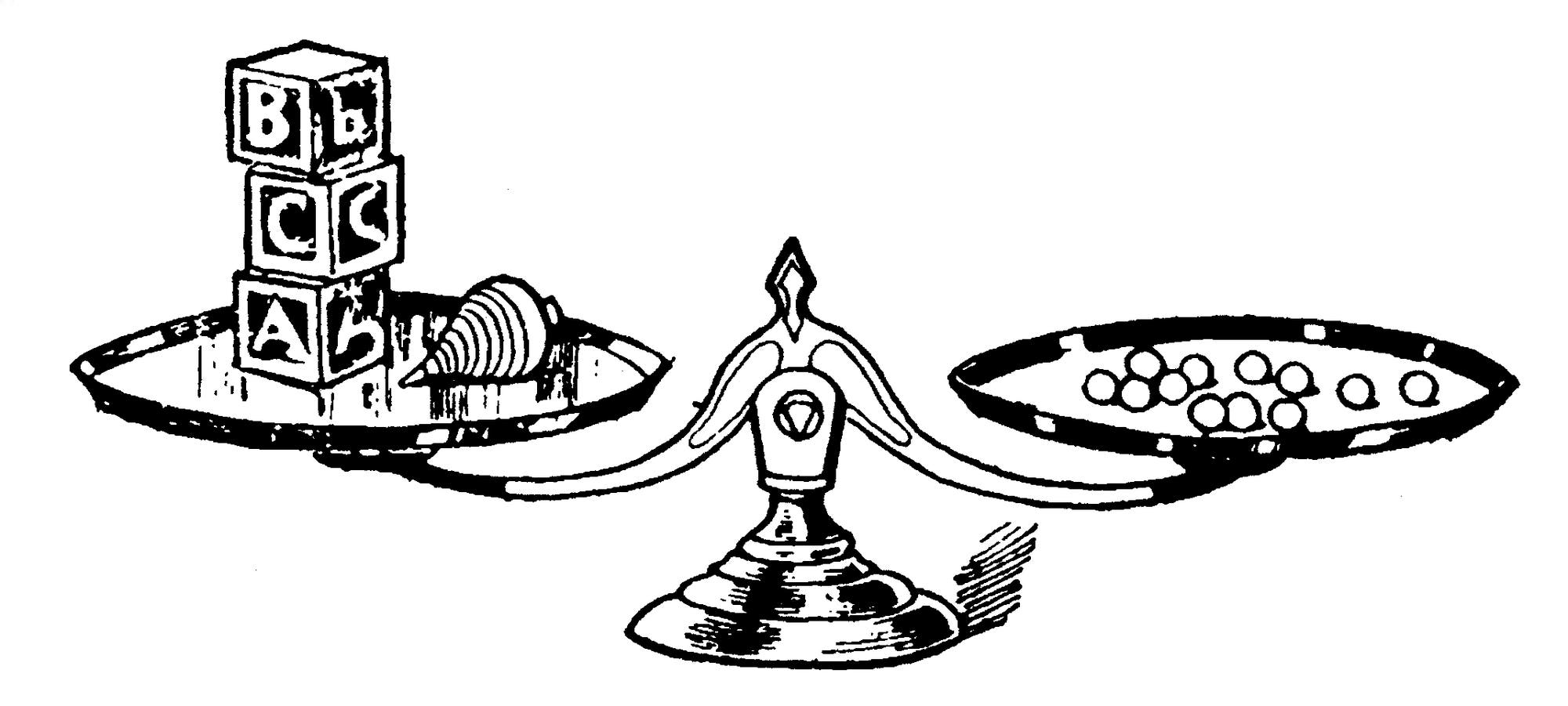
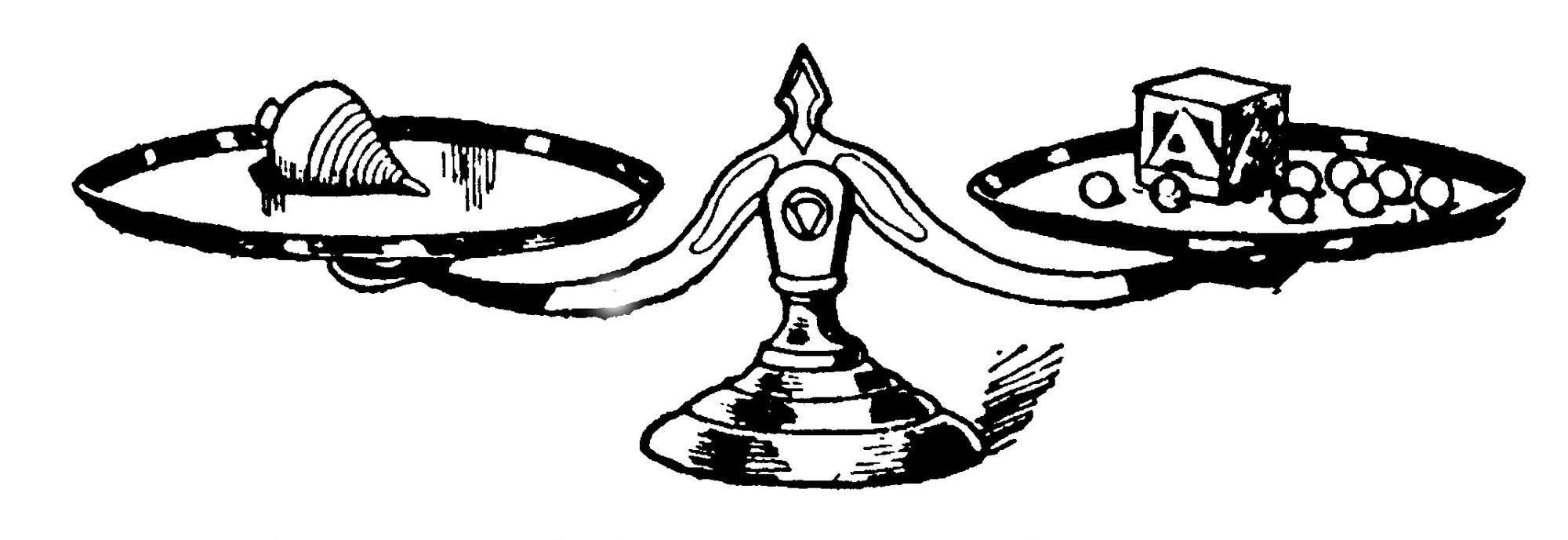
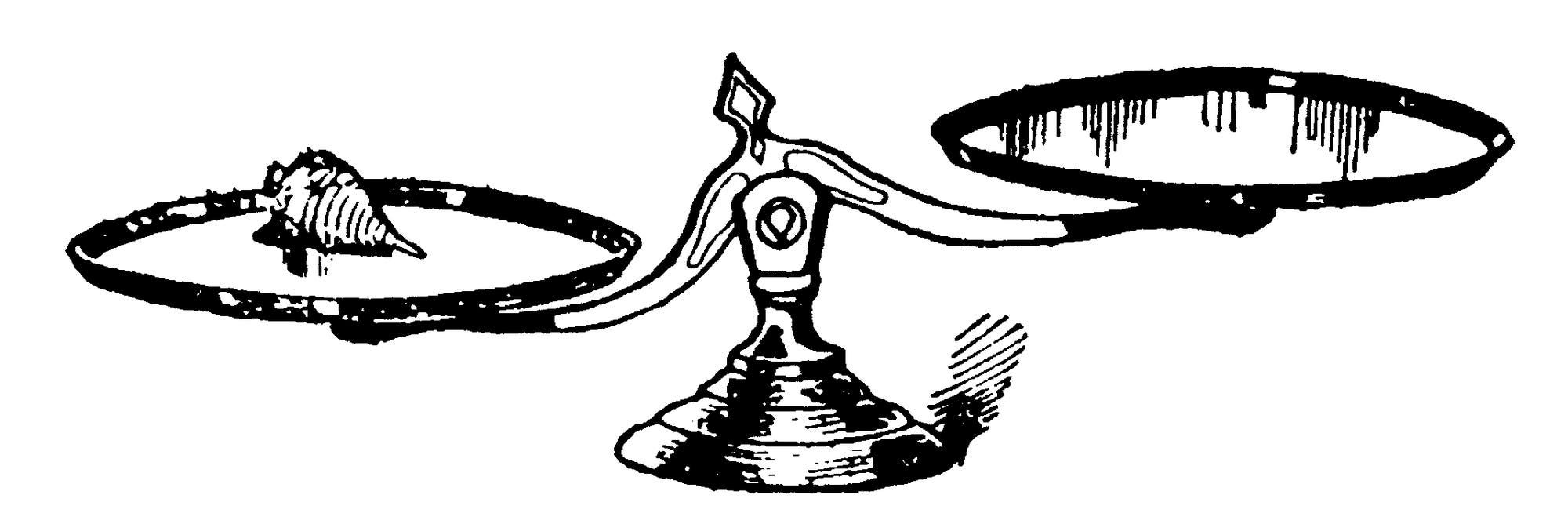
Auf den Schalen von zwei Waagen sind Würfel, Kreisel und Murmeln so verteilt, dass sie beide im Gleichgewicht sind. Wie viele Murmeln muss man auf die rechte Schale der dritten Waage legen, damit auch diese im Gleichgewicht ist?
Bei der ersten Waage aus der Aufgabe kann man sehen, dass drei Würfel (W) und ein Kreisel (K) genauso schwer sind wie zwölf Murmeln (M). Dies lässt sich auch durch die Gleichung 3W + K = 12M darstellen.
Die zweite Waage kann man durch die Gleichung K = W + 8M beschreiben. Löst man sie nach W auf, erhält man W = K − 8M.
Dies eingesetzt in die erste Gleichung ergibt 3(K − 8M) + K = 12M. Nach K aufgelöst ergibt sich nun K = 9M. Man muss also neun Murmeln auf die rechte Schale der dritten Waage legen, um sie ins Gleichgewicht zu bringen.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.