Die Bewegungsenergie ist abhängig von der Geschwindigkeit und damit auch vom Bezugssystem, relativ zu dem die Geschwindigkeit gemessen wird.

Die Erhaltung der Energie gilt für jedes Bezugssystem, aber das schließt ja nicht aus, dass der Planet der Sonde etwas von seiner Bewegungsenergie abgibt.

Wählen wir zunächst das spezielle Bezugssystem, in dem der gemeinsame Schwerpunkt von Planet und Sonde die Geschwindigkeit 0 hat (SPS = Schwerpunktsystem). Zu jedem Zeitpunkt während des Abfliegens gibt es einen Zeitpunkt während des Anfliegens, zu dem der Abstand zwischen Sonde und Planet der gleich ist, und damit auch die Schwereenergie. Also hat die Sonde zu diesen beiden Zeitpunkten die gleiche Bewegungsenergie und damit auch den gleichen Geschwindigkeitsbetrag; ebenso ergeht es dem Planeten.

Von diesem gemeinsamen Schwerpunkt aus gesehen – und damit praktisch auch vom Planeten aus – überträgt die Begegnung also keine Energie vom Planeten zur Sonde oder umgekehrt (wohl aber Impuls). Für die Reisen von Raumsonden durch das Sonnensystem zu fernen Planeten ist aber die heliostatische Bewegungsenergie – also relativ zur Sonne – entscheidend und nicht diejenige relativ zu einem Planeten, dem sie sich zwischendurch nähert. Gerade deswegen kann diese Begenung genutzt werden, um der Sonde etwas (relativ zur Sonne gemessene) Energie von diesem Planeten zu übertragen.

Betrachten wir einen idealisierten Fall: Die Sonde läuft – heliostatisch gemessen – mit 10 km/s fast frontal auf einen Planeten zu, der ihr mit 20 km/s entgegenkommt. Im SPS von Planet und Sonde sind das 30 km/s. Die Bahn der Sonde ist in diesem SPS ein Hyperbelast, der im Extremfall fast wie eine Haarnadel die Richtung umkehrt. Ganz erreichbar ist dieser Fall nicht, weil die Objekte dazu punktförmig sein müssten, aber für die idealisierte Abschätzung ist das nicht wesentlich. Die Sonde läuft nach der Begegnung also mit 30 km/s fast in die entgegengesetzte Richtung – vom Planeten aus gesehen. Heliostatisch sind das aber nun 50 km/s, nämlich 30 km/s mehr als die Geschwindigkeit des Planeten, die praktisch unverändert 20 km/s in der bisherigen Richtung ist.

Allgemeiner gesagt, kann die Sonde heliostatisch ihren Geschwindigkeitsbetrag fast um das Doppelte der Geschwindigkeit des Planeten erhöhen, exakt könnte sie das, wenn sie ihre Richtung genau um 180^o umkehren könnte. Dabei ist vorausgesetzt, dass die Masse der Sonde verschwindend klein gegen die des Planeten ist, was ja in der Praxis stets erfüllt ist. Tatsächlich wird dieser Trick genutzt, um Fernsehkameras zu den entfernten Planeten und ihren Satelliten zu schicken.

Die teilweise Umrundung ist gewissermaßen ein Stoß mit Anziehungskräften. Wenn ein Kind die Treppe herunterrennt und an einem Absatz wenden muss, so kann es entweder gegen eine Wand laufen und sich von dieser abstoßen, oder es kannsich um eine Säule am Ende des Geländers herum schleudern, wobei dann die Arme auf Zug beansprucht werden.

Dazu eine Animation

Die blauen Pfeile zeigen die Geschwindigkeiten, die Flächen der Quadrate die Bewegungsenergien der Sonde. Beachten Sie, dass diese im SPS auf Hin- und Rückweg bei jeweils gleichen Entfernungen gleich sind, im heliostatischen System aber nicht. Die roten Pfeile zeigen die Gravitationskraft an. Die Animation ist mit dem Gravitationsgesetz gerechnet.

Zum Verständnis der Lösung brauchen Sie – außer den im Tipp angegeben Regeln – an Voraussetzungen nur die Umrechnung der Geschwindigkeit beim Wechsel eines Bezugssystems und die Tatsache, dass die Bewegungsenergie umso größer ist, je größer der Betrag der Geschwindigkeit ist. Von der Schwerkraft muss man hier nur wissen, dass die zu ihr gehörende Energie nur vom Abstand der beiden Objekte abhängt.

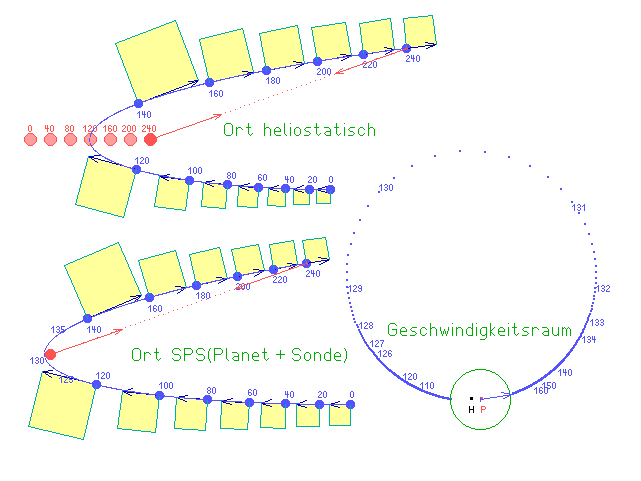
Hier ist noch einmal die Bewegung zusammengefasst, die Zahlen bedeuten Zeitpunkte in gleichen Abständen, und das Geschwindigkeitsdiagramm ist größer gezeichnet: Die Kurve darin ist auch theoretisch ein Kreis! H und P sind darin die Nullpunkte für die Geschindigkeit relativ zur Sonne bzw. relativ zum Planeten (und damit dem gemeinsamen SPS von Planet und Raumsonde).

Das nächste Bild zeigt die Geschwindigkeiten lange vor und lange nach dem "Stoß", also Anfang und Ende des großen Kreisbogens am kleineren grünen Kreis im vorigen Bild. Die Geschwindigkeit der Sonde vor dem "Stoß" ist weitgehend beliebig, relativ zum Planeten (eigentlich zu dem mit ihm gemeinsamen SPS) muss der Betrag "lange nach dem Stoß" wieder so sein wie "lange vor dem Stoß", der grüne Kreis zeigt diesen gleichen Betrag an. (In 3 Dimensionen ist der Kreis durch eine Kugel zu ersetzen, aber die kann man in eine Ebene drehen, in der sich alles abspielt.) Relativ zum Sonnensystem (heliostatisch) kann das aber eine drastische Änderung des Geschwindigkeitsbetrages sein, und genau das ist ja der Sinn der Sache.

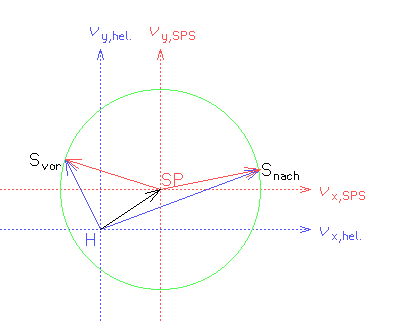
Wenn es keine Schwerkraft gäbe und der Planet mit einem idealen Trampolin ausgestattet wäre, könnte man den Swingby auch durch elastische Abstoßung ersetzen.