Es gibt 13 konvexe Polygone (d. h. ohne einspringende Ecken) aus jeweils allen 7 Tangram-Steinen, einige sind auf mehrere verschiedene Weisen erzeugbar (abgesehen von Spiegelungen). Es handelt sich um 1 Dreieck, 6 Vierecke (darunter das schon vorgelegte Quadrat und ein anderes Rechteck), 2 Fünfecke und 4 Sechsecke.

Um zu vermeiden, dass Sie versehentlich etwas Ungenaues tun, ist es empfehlenswert, alle Teile aus dem Quadrat nur um 90^o zu drehen oder auch umzuklappen, aber nicht um 45^o (etc.) zu drehen. Dann liegen auch alle Ecken in einem einfachen Raster.

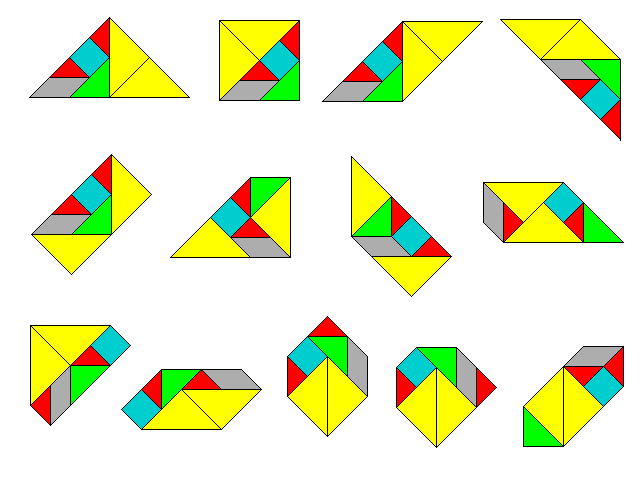
Es ist noch anzumerken, dass alle diese Figuren auch gelegt werden können, wenn eins der kleinsten Dreiecke und das Quadrat fest zusammenhängen, sozusagen beim Schneiden der 7 Teile gar nicht getrennt wurden (gefunden bei Coffin und im Bild leicht zu bestätigen).

Dass es genau 13 konvexe Figuren aus den Tangram-Steinen gibt, haben Fu Triang Wang und Chuan-Chih Hsiung 1942 gezeigt (Amer. Math. Monthly 49, 596-599, 1942) und dabei als Hilfssatz benutzt, dass die Teile stets um Vielfache von 90^o gegeneinander gedreht sein müssen (und nicht von 45^o).