Hemmes mathematische Rätsel: Trioker-Sechsecke
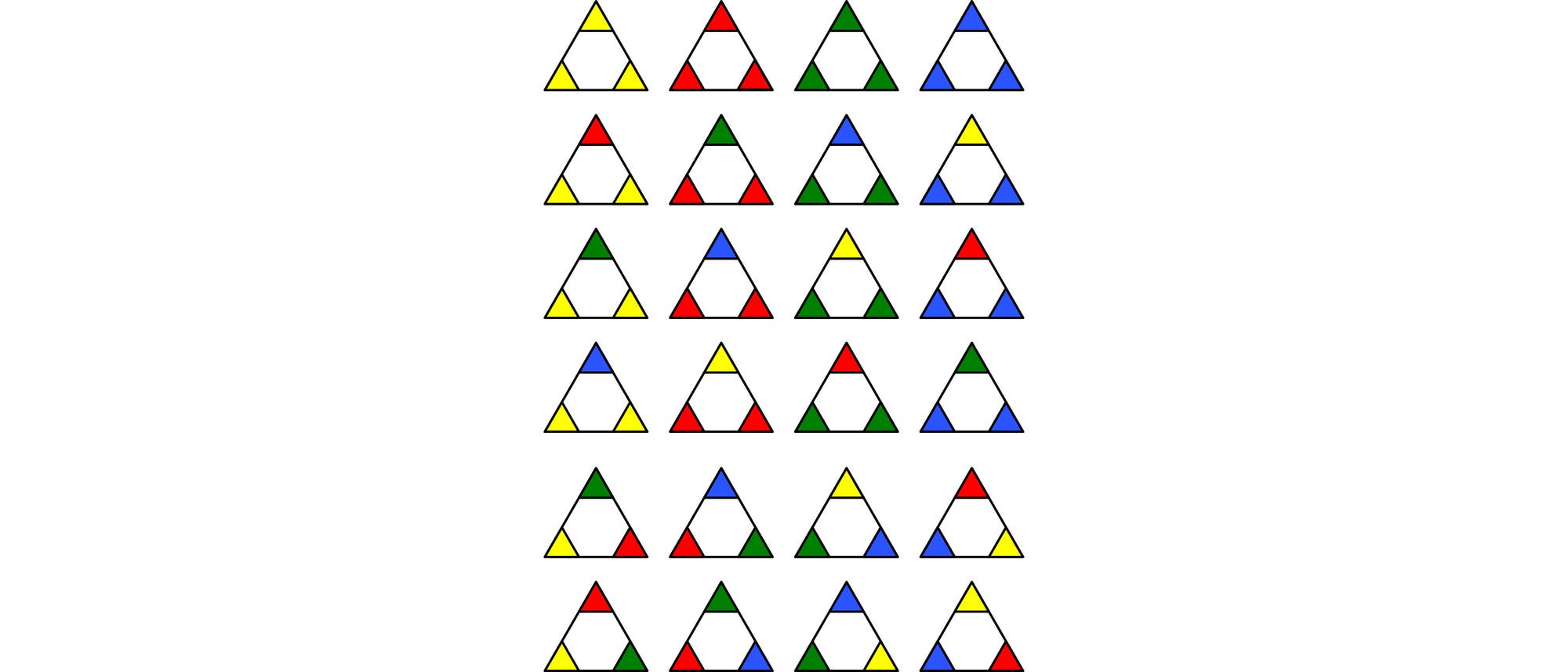
Trioker ist Spiel, das unter mehreren Namen und unterschiedlichem Aussehen bekannt ist. Um 1970 war es in Frankreich recht populär. Es besteht aus 24 dreieckigen Spielsteinen mit farbigen Ecken.
Die Steine werden wie Dominosteine mit den Kanten aneinander gelegt. Dabei dürfen jedoch nur gleichfarbigen Ecken aufeinander treffen. Sechs Steine kann man beispielsweise zu einem Sechseck auslegen. Dafür gibt es zahlreiche Möglichkeiten. Die untere Abbildung zeigt eine davon.
Wählen Sie von den 24 Steinen zwölf aus und legen Sie diese zu zwei Sechsecken zusammen, die beide in der Mitte rot sind. Die beiden Sechsecke brauchen sich nicht zu berühren. Wie viele verschiedene Möglichkeiten gibt es hierfür? Sechsecke, die durch Drehung ineinander übergehen, zählen als gleich. Spiegelbildliche Muster sind jedoch verschieden.
Beim Triokerspiel gibt es 13 Steine, die mindestens eine rote Ecke haben. Diese 13 Steine haben zusammen 39 Ecken, von denen 18 rot und 7 gelb, 7 blau und 7 grün sind.
Zieht man die 12 Mittelecken der beiden Sechsecke ab, bleiben für Ränder 6 rote, 7 gelbe, 7 blaue und 7 grüne Ecken übrig. Die Farben treten an den Sechsecksecken jeweils paarweise auf. Folglich wird von jeder Farbe eine gerade Anzahl benötigt.
Einer der 13 Steine wird nicht benötigt. Damit alle Farben geradzahlig häufig auftreten, müsste man einen Stein mit einer gelben, einer blauen und einer grünen Ecke fortnehmen. Diesen gibt es allerdings nicht bei den 13 Steinen. Folglich ist das Problem unlösbar.
Schreiben Sie uns!
Beitrag schreiben