Trojaner

Die Bewegung von mehr als zwei (punktförmigen) Objekten im gemeinsamen Schwerefeld ist im Allgemeinen nicht ohne Näherungsverfahren berechenbar: Das ist das berüchtigte Dreikörperproblem. Aber es gibt lösbare Spezialfälle. Einer davon ist realisiert in Gestalt einiger Kleinplaneten, die die gleiche Umlaufperiode wie Jupiter haben und nach Streitern aus dem Trojanischen Krieg benannt sind.
Die allgemeine Aussage ist die folgende: Drei Punktmassen können beim Umlauf um ihren gemeinsamen Schwerpunkt ein starr drehendes gleichseitiges Dreieck bilden.
Der Beweis geht erstaunlich einfach und fast ohne Rechnung.
Zeichnen Sie in dem Dreieck aus den drei Objekten Parallelen zu den Seiten und zeichnen Sie in dieses Bild in passendem Maßstab Pfeile für die Beschleunigung, die jeder Masssenpunkt auf jeden anderen ausübt, und dann für die resultierende Beschleunigung, die jeder von den beiden anderen zusammen erfährt.
Wegen der gleichen Abstände der Objekte voneinander (und nur dann klappt es!) ist die Beschleunigung, die jeder Massenpunkt seinen Partnern erteilt, einfach proportional zu dessen Masse, und die Resultierenden zeigen auf den gemeinsamen Schwerpunkt aller drei Objekte. Im Bild sind die Beschleunigungspfeile in einem solchen Maßstab gezeichnet, dass ihre Spitzen diesen Schwerpunkt treffen.
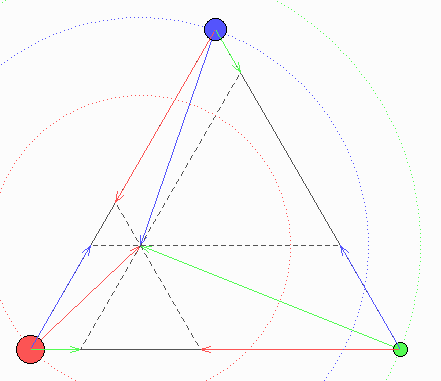
Von der Zentripetalbeschleunigung auf Kreisbahnen wissen wir, dass sie für gleiche Winkelgeschwindigkeit proportional zum Bahnradius sein muss. Genau das ist hier laut Zeichnung der Fall.
Bemerkenswerterweise können die drei Massen beliebig sein. Im realen Fall sind sie sehr verschieden. Mit der Sonne und Jupiter gibt es nicht nur ein gleichseitiges Dreieck in ihrer Bahnebene, sondern deren zwei: Eine Ecke läuft dem Jupiter um 60 Grad voraus, die andere 60 Grad hinterher um den gemeinsamen Schwerpunkt aller beteiligten Objekte (also vor allem von Sonne und Jupiter). Die Kleinplaneten laufen keineswegs auf diesen Ecken, sondern schwanken langfristig um diese Ecken herum, und zwar laufen sie in einem Bezugssystem, in dem Sonne und Jupiter festgehalten werden, auf nierenförmigen Bahnen um die Ecken der Dreiecke herum (im Inertialsystem natürlich auf kreisnahen Kurven um den Schwerpunkt des Sonnensystems).
1772 fand Lagrange die theoretische Möglichkeit dieser exakten Lösungen des Dreikörperproblems (und die einfachere Lösung mit drei Objekten auf einer Geraden), die zugehörigen Kleinplaneten wurden aber erst im 20. Jahrhundert gefunden.
Die dem Jupiter vorauslaufenden Kleinplaneten sind Achilles, Agamemnon, Ajax, Antilochus, Diomedes, Menelaos, Nestor, Odysseus (alle nach Griechen benannt) und Hektor. Die dem Jupiter nachlaufenden sind Aeneas, Anchises, Priamus, Troilus (nach Trojanern benannt) und Patroklus. Vielleicht hat die Inkonsequenz der Namenszuordnungen (Hektor und Patroklus bei den damaligen Feinden einsortiert) auch etwas Versöhnliches. Im Gegensatz zu den Sagengestalten, deren Gewalttaten zu verherrlichen immer noch als humanistische (!) Bildung gilt, sind die Kleinplaneten ausgesprochen friedlich.



Schreiben Sie uns!
Beitrag schreiben