Viereck im Rechteck
© Norbert Treitz (Ausschnitt)
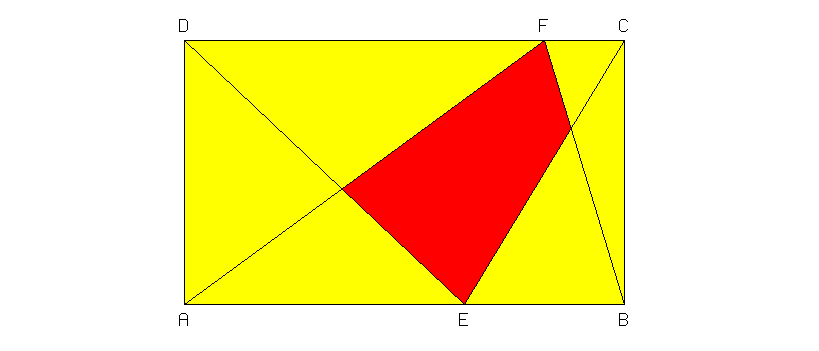
Verschieben Sie die Punkte E und F in diesem Rechteck so, dass das rote Viereck möglichst groß wird.
Lassen Sie zunächst nur einen der Punkte E oder F wandern.
© Norbert Treitz (Ausschnitt)
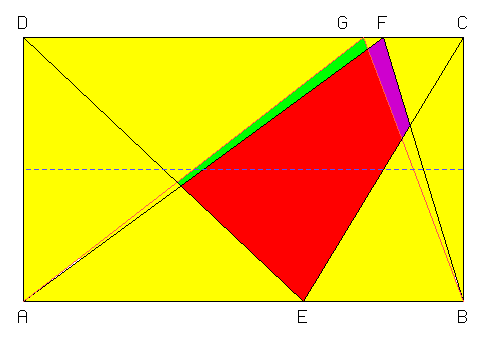
Hier wandert nur F, und zwar nach G. Da die Dreiecke AGF und BGF gleich groß sind, ist die grüne Fläche größer als die violette. Daraus ist sogleich zu sehen, dass die rote Fläche (bei festgehaltenem E) maximal wird, wenn F und E symmetrisch zur waagerechten Achse des Rechtecks liegen.
Wo aber müssen diese liegen?
© Norbert Treitz (Ausschnitt)
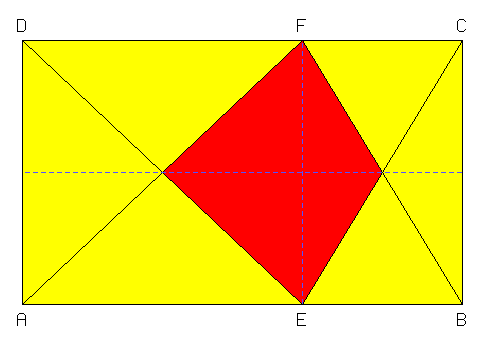
E und F können für das Optimum irgendwo auf AB beziehungsweise DC liegen, aber es muss – wie gezeigt – AE = DF sein. Die rote Fläche ist dann in jedem Fall 1/4 der Fläche des ganzen Rechtecks.



Schreiben Sie uns!
Beitrag schreiben