Der Mathematische Monatskalender: Jakob Steiner (1796–1863)

Jakob Steiner wächst als jüngstes von acht Kindern auf dem Bauernhof seiner Eltern in Utzenstorf (Nähe Bern) auf. Der Unterricht in der Volksschule beschränkt sich in den ersten Jahren auf das Auswendiglernen des Kathechismus und des Gesangbuches. Erst mit 14 Jahren lernt Jakob lesen und schreiben; das Rechnen bringt er sich selbst bei, wenn er die Erzeugnisse des Bauernhofs auf dem Markt verkauft. Mit 18 Jahren verlässt der wissbegierige Jugendliche das Elternhaus, um die Schule des Reformpädagogen Johann Heinrich Pestalozzi in Yverdon im Kanton Waadt zu besuchen. Die an der Schule praktizierten Lehr- und Lernmethoden ("Lernen mit Kopf, Herz und Hand") tragen dazu bei, seine Fähigkeiten zur Entfaltung zu bringen; nach nur eineinhalb Jahren wird Jakob damit beauftragt, Unterricht zu übernehmen.
Als die Schule in Yverdon aufgelöst wird, geht Steiner zum Mathematik-Studium nach Heidelberg; seinen Lebensunterhalt bestreitet er als Privatlehrer. 1821 folgt er einem Angebot, als Aushilfslehrer am Friedrichswerderschen Gymnasium in Berlin tätig zu werden. Dort bleibt er jedoch nicht lange: Der Schulleiter, selbst Mathematiker, besteht darauf, dass der Unterricht genauestens nach dem von ihm verfassten Schulbuch ablaufen soll. Da Steiner von Pestalozzis Methode überzeugt ist, die Schüler mathematische Sachverhalte möglichst selbst entdecken zu lassen, und sich dies nicht mit der Vorgehensweise des Buches vereinbaren lässt, wird er nach wenigen Wochen wieder entlassen.
Der Autodidakt Steiner bemüht sich um eine formale, offizielle Zulassung als Lehrer. Mit den Anforderungen im Fach Mathematik hat er keine Probleme, allerdings scheitert er wegen fehlender Kenntnisse in Philosophie, Geschichte und Literatur, die von ihm erwartet werden. Er schreibt sich an der Berliner Universität ein; seinen Lebensunterhalt verdient er als Privatlehrer, darunter im Hause Wilhelm von Humboldts, bis er endlich eine Stelle als Hilfslehrer an der neu eingerichteten Gewerbeakademie findet (vergleichbar mit einer späteren Oberrealschule).
Steiners Schulleiter, Karl Friedrich von Klöden, ebenfalls Mathematiker und auch Anhänger der Pädagogik Pestalozzis, überlässt ihm nach und nach sogar den Unterricht in den Abschlussklassen.
1826 gründet August Leopold Crelle das Journal für die reine und angewandte Mathematik. Für die erste Ausgabe der Zeitschrift verfasst Steiner gleich vier Beiträge; im Laufe der Jahre werden noch 58 weitere hinzukommen. Eine dieser Abhandlungen beschäftigt sich mit der Frage, in wie viele "Teile" der Raum durch \(n\) Ebenen unterteilt werden kann. Steiner zeigt, dass die maximale Anzahl \(\ \frac{1}{6}(n^3 + 5n + 6)\ \) beträgt.
Auch Niels Henrik Abel veröffentlicht mehrere Beiträge in Crelles Journal (vor seinem frühen Tod im Jahre 1829). Wenn Crelle zusammen mit den beiden jungen Gelehrten in der Öffentlichkeit gesehen wird, heißt es im Berliner Volksmund "Adam geht wieder mal mit seinen Söhnen Kain und Abel spazieren".
Im Jahr 1826 erhält Steiner endlich eine offizielle Unterrichtserlaubnis; die zuständige Kommission beeindruckt er durch die von Crelle angenommenen Artikel.
Da er seine Ideen zur Geometrie ausarbeiten und in Buchform veröffentlichen möchte, stellt er einen Antrag an das Ministerium, ihm einen Zuschuss für die Druckkosten zu gewähren. Im Antrag schreibt er: "Die neue Betrachtungsweise, welche die geometrisch-synthetische Methode selbst betrifft, unterscheidet sich übrigens von dem älteren Verfahren insbesondere dadurch, dass sie nicht bloß, wie dieses, den Zusammenhang einzeln gebildeter Sätze nachweiset, und die Wahrheit des einen durch die des anderen darthut: sondern dass sie die Sätze unmittelbar auseinander entstehen lässt und durch einen genetischen Gang auf eine vollständigere Weise die Form des synthetischen Entstehens offenbart, als die ältere, seit den Griechen gewöhnliche Methode." – Klöden befürwortet den Antrag mit begeisterten Worten; er stellt Steiners Manuskripte sogar über die verloren gegangenen Schriften des Apollonius von Perge.
Friedrich Wilhelm Bessel, Professor in Königsberg, um eine Stellungnahme gebeten, merkt an "... allein wenn er auch Poncelets Werk gewiss kennt, so haben seine Aufsätze so viel Originelles, dass man sie als selbstständig ansehen und namentlich die Einbildungskraft bewundern muss, womit er die Eigenschaften der Figuren und Oberflächen sich vor Augen zu bringen weiß."
Der französische Mathematiker und Ingenieur Jean-Victor Poncelet hatte 1823 mit seiner Schrift Traité des propriétés projectives des figures die Grundlagen der projektiven Geometrie geschaffen. In seinem ersten Buch Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von einander aus dem Jahr 1832 entwickelt Steiner diese Ideen konsequent weiter. Bessel und Carl Gustav Jacob Jacobi, mit dem Steiner seit seiner Studienzeit an der Berliner Universität befreundet ist und seit 1827 ebenfalls Professor in Königsberg, sorgen dafür, dass dieser geniale Beitrag Steiners durch die Ehrendoktorwürde der Universität Königsberg eine besondere Anerkennung findet.
In der Zwischenzeit hat sich jedoch Steiners Position in der Gewerbeschule – trotz seiner Beförderung zum Oberlehrer – dramatisch geändert. Immer häufiger werden die Beschwerden über seine grobe und beleidigende Art im Umgang mit Schülern und Kollegen. Der Direktor Klöden sieht seine Amtsautorität untergraben, als Steiner in seinen Klassen ohne Absprache die Unterrichtsinhalte ändert und sogar sein neu erschienenes Buch für seine Prima zum verbindlichen Schulbuch erklärt. Schließlich droht ihm sogar die Entlassung aus dem Schuldienst.
Nach der Veröffentlichung seines zweiten Buches (Die geometrischen Constructionen ausgeführt mittels der geraden Linie und eines festen Kreises) im Jahre 1833 beantragt Steiner, der durch Schuldienst und gleichzeitige wissenschaftliche Arbeit überlastet ist, einen Genesungsurlaub, der ihn in seine alte Heimat führt. An der neu gegründeten Universität Bern führt er Gespräche über eine mögliche Professur, auch um nach seiner Rückkehr in Berlin eine bessere Verhandlungsposition zu haben. Als schließlich einer der Ordinarien der Universität stirbt und ein anderer (Julius Plücker) einen Ruf nach Halle annimmt, wird für Steiner der ersehnte Weg frei: Alexander und Wilhelm von Humboldt sorgen dafür, dass für ihn eine außerordentliche Professur eingerichtet wird (1834). Crelle und Gustav Lejeune Dirichlet kümmern sich um die Aufnahme Steiners in die Preußische Akademie der Wissenschaften.
Auch Steiners zweite große Veröffentlichung erregt Aufsehen; sie beschäftigt sich mit den Konstruktionen der euklidischen Geometrie. Er zeigt, dass hierfür ein Lineal (ohne Maßstab) genügt, sobald ein fester Kreis gezeichnet ist, man also auf die weitere Nutzung eines Zirkels verzichten kann.
In den Folgejahren erscheinen allerdings nur noch kleinere Abhandlungen; das von ihm bereits 1830 angekündigte siebenbändige Werk zur Geometrie kommt niemals zustande. Posthum veröffentlichte Ausarbeitungen seiner Vorlesungen vermitteln eine Vorstellung von dem, was er im Einzelnen plante.
Für Algebra und Analysis hat Steiner nicht viel übrig; er vertritt die Meinung, dass das in diesen Disziplinen übliche "Rechnen" das Denken ersetzt, während die Beschäftigung mit den Konstruktionen und Schlussfolgerungen der synthetischen Geometrie zum Denken anregt – im Unterschied zur analytischen Geometrie, in der ebenfalls "gerechnet" wird. ("Die Analysis zieht einem die Schlafkappe über den Kopf. Bei uns heißt es: Augen aufsperren, dann sieht man die Sachen auch.")
Seit dem Altertum beschäftigen sich Geometer mit dem sogenannten isoperimetrischen Problem (iso = gleich, perimeter = Umfang): Welche Form hat eine geschlossene Kurve mit fester Länge, welche die größte Fläche einschließt? Während eines Paris-Aufenthalts 1840/41 veröffentlicht er fünf Beweise, dass der Kreis diese Eigenschaft hat (äquivalente Aussage: Von allen Kurven, die denselben Flächeninhalt umschließen, hat der Kreis den kleinsten Umfang), darunter auch ein rein geometrischer Beweis. Diesen führt er, indem er zeigt, dass die einschließende Kurve konvex und in beliebiger Richtung symmetrisch sein muss. (Karl Weierstraß schließt eine Beweislücke, nämlich zu zeigen, dass überhaupt eine Lösung existiert.) Steiner beweist auch, dass unter allen Körpern mit fester Oberfläche die Kugel das größte Volumen hat (äquivalent: ... mit festem Volumen die kleinste Oberfläche).
1848 veröffentlicht er einen nur kurzen, aber genialen Beitrag Allgemeine Eigenschaften algebraischer Curven – allerdings ohne Beweise. So sind noch Generationen von Mathematikern mit der Überprüfung der Richtigkeit der Aussagen beschäftigt. Da Steiner in seiner Jugend keine Gelegenheit hatte, eine Fremdsprache zu lernen, ist er nicht in der Lage, Fachartikel zu lesen, die in anderen Sprachen verfasst sind (Pflichtsprache für Dissertationen an der Berliner Universität ist in dieser Zeit immer noch das Lateinische). Recherchen darüber, ob bereits etwas über einen von ihm neu entdeckten Sachverhalt veröffentlicht wurde, überlässt er Jacobi; allerdings verhält er sich in seiner Zitierweise nicht immer korrekt.
Sein Antrag auf Umwandlung der außerordentlichen Professur in eine ordentliche wird mehrfach aus haushaltsrechtlichen Gründen abgelehnt; möglicherweise spielt dabei auch eine Rolle, dass ihm die für einen Hochschullehrer erwartete akademische Bildung fehlt. Auch als Hochschullehrer erweist sich Steiner als schwierig; Zeitgenossen beschreiben sein hitziges Temperament, seine begeisternde Art, über Mathematik zu reden, aber auch seine manchmal groben, befremdlich-schroffen Umgangsformen. Schließlich liegt er sogar mit seinem Freund Jacobi im Streit.
In den letzten Jahren seines Lebens verschlechtert sich Steiners Gesundheitszustand zusehends; Kuraufenthalte wegen seines Nierenleidens bleiben ohne Wirkung. Die meiste Zeit verbringt er in seiner Schweizer Heimat; nur während der Vorlesungsmonate hält er sich in Berlin auf. Als er 1863 in Bern einsam stirbt, hinterlässt der Junggeselle ein kleines Vermögen, das er zu einem Drittel der Berliner Akademie vermacht; von den Zinsen wird der nach ihm benannte Steiner-Preis finanziert. Ein kleiner Teil des Erbes wird dafür verwendet, an seiner alten Volksschule in Utzenstorf regelmäßig einen Wettbewerb durchzuführen und die besten Kopfrechner auszuzeichnen.
Heute erinnern noch zahlreiche Begriffe an die Themen, mit denen sich der geniale Mathematiker beschäftigt hat:
Das Steiner-Baum-Problem beschäftigt sich mit der Frage, durch welchen Graph \(n\) Punkte so miteinander verbunden werden können, dass das kürzeste Wegenetz entsteht; dabei dürfen auch \(n- 2\) zusätzliche Punkte eingefügt werden (Steiner-Punkte). Für \(n = 3\) war das Problem bereits von Evangelista Torricelli und Pierre de Fermat gelöst worden: Wenn alle Innenwinkel des zugehörigen Dreiecks kleiner sind als 120°, dann bilden die Verbindungsstrecken zu dem zusätzlichen Punkt jeweils einen Winkel von 120°. Wenn einer der Innenwinkel des Dreiecks gleich 120° oder größer ist, dann ist die Summe der Streckenlängen zu diesem Punkt minimal. Die Abbildungen zeigen die optimalen Lösungen für das gleichseitige Dreieck, für ein Rechteck sowie für das reguläre Fünfeck.
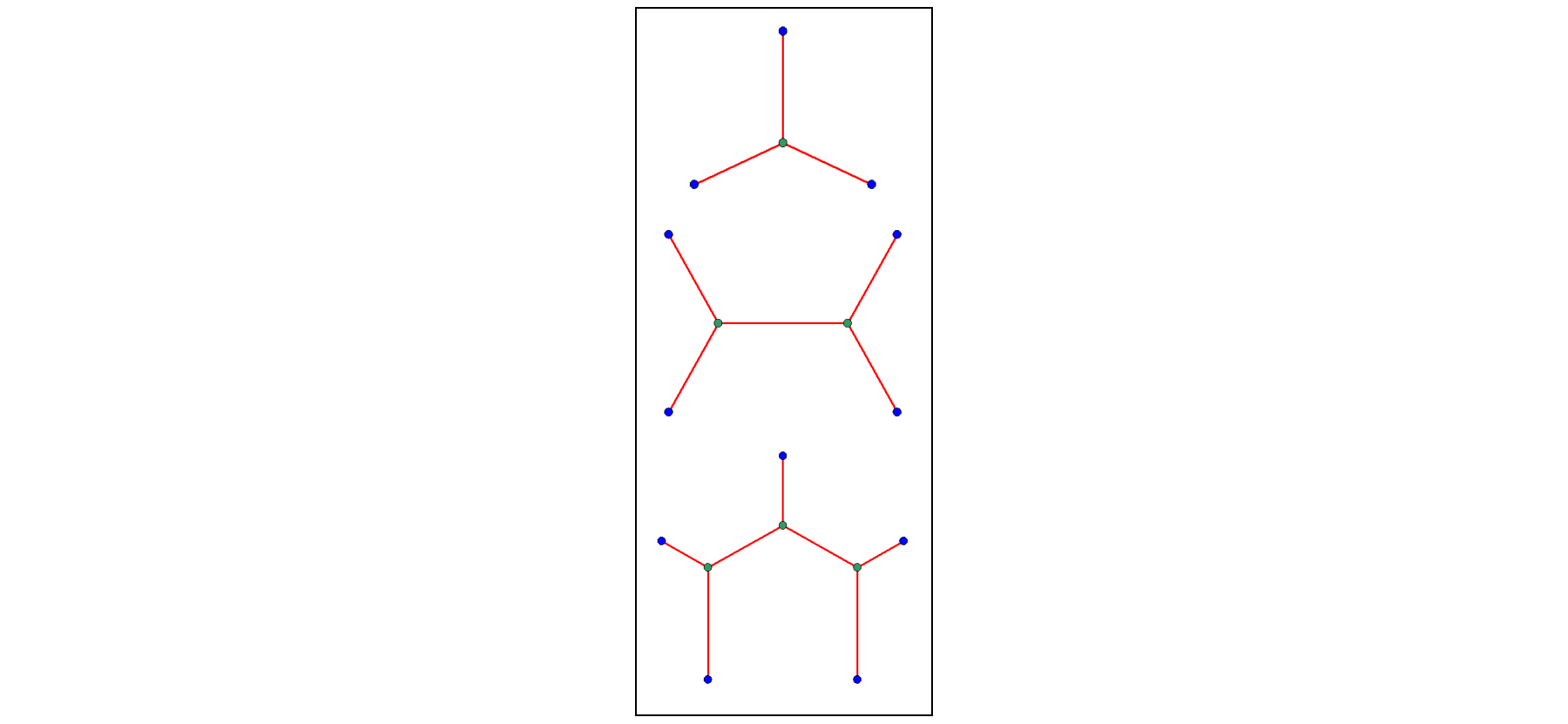
Für beliebige Anzahlen \(n\) gehört das Problem zu den 21 klassischen NP-vollständigen Problemen, das heißt, es ist im Allgemeinen aussichtslos, eine optimale Lösung in endlicher Rechenzeit zu finden.
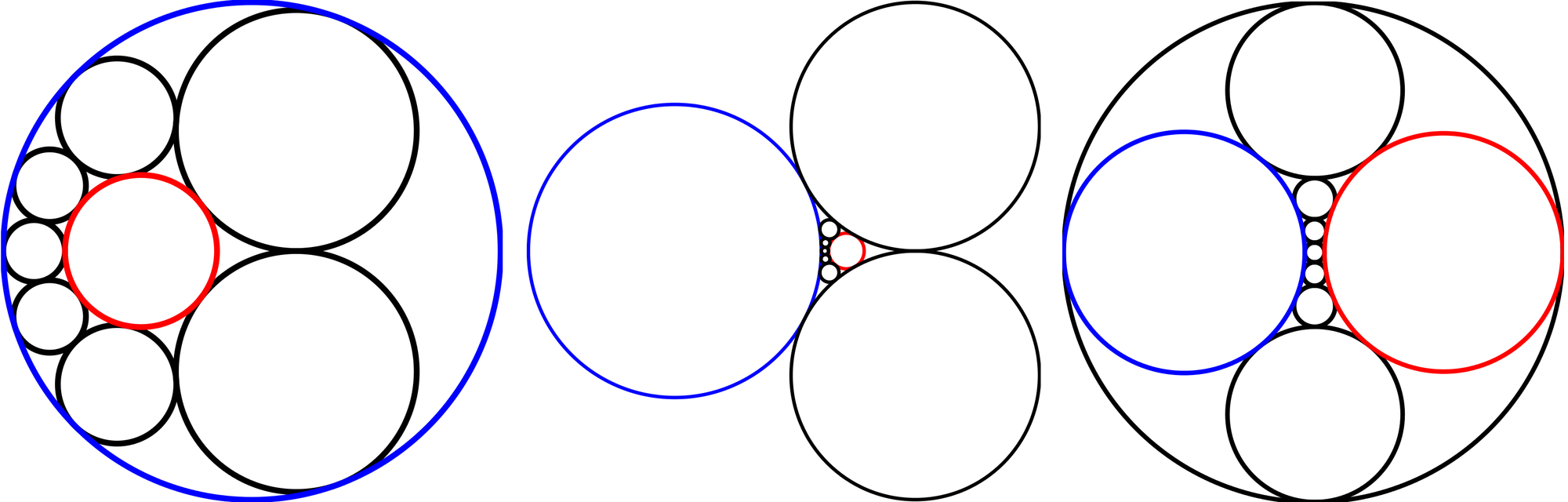
Als (geschlossene) Steiner-Kette bezeichnet man eine zusammenhängende Folge von endlich vielen, einander berührenden Kreisen, die zwei vorgegebene, sich nicht schneidende Kreise berührt. Steiner beweist den bemerkenswerten Satz: Wenn zwischen zwei Ausgangskreisen eine solche Steiner-Kette möglich ist, dann auch unendlich viele. Die Berührungskreise der Kreise liegen auf einem Kreis, die Mittelpunkte der Kreise auf einem Kegelschnitt.
Als Steiner-Ellipsen werden die Ellipsen mit maximalem beziehungsweise minimalem Flächeninhalt bezeichnet, die einem gegebenem Dreieck ein- beziehungsweise umbeschrieben werden können (die Inellipse berührt die Seiten jeweils in der Seitenmitte, der Schwerpunkt des Dreiecks ist der Mittelpunkt der Umellipse). Für die Flächeninhalte gilt: \( A_{ein}=\frac{\pi}{\sqrt{27}}\cdot A_\Delta\) beziehungsweise \(A_{um}=\frac{4\pi}{\sqrt{27}}\cdot A_\Delta\)
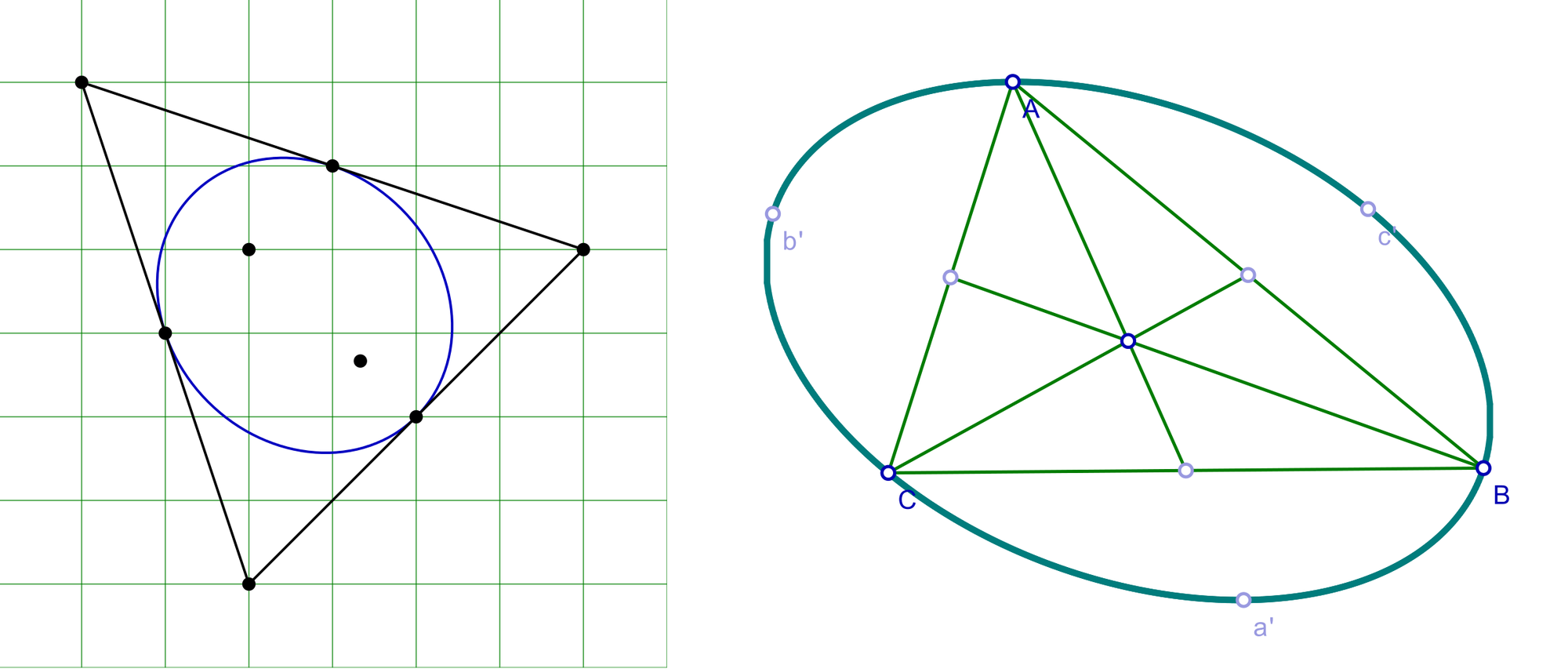
rechts: Claudio Rocchini / Steiner-Ellipse / CC BY-SA 3.0, CC BY-SA (Ausschnitt)
In der Physik wird der Satz von Steiner angewandt, wenn es darum geht, das Trägheitsmoment eines starren Körpers der Masse \(m\) zu berechnen: Kennt man das Trägheitsmoment \(J_S\) bezüglich einer Drehachse, die durch den Schwerpunkt des Körpers verläuft, dann berechnet sich das Trägheitsmoment \(J_d\) einer im Abstand \(d\) parallel verlaufenden Drehachse mithilfe von \(\ J_d = J_S + m \cdot d^2\).
Als Steiner'sche Flächen werden spezielle Flächen im Raum bezeichnet, auf deren Oberflächen Scharen von Kegelschnitten liegen. Während eines gemeinsamen Studienaufenthalts in Rom im Jahre 1844 (zusammen mit Dirichlet und Jacobi) untersuchte Steiner eine spezielle Fläche, von ihm auch Römische Fläche genannt, die durch die Gleichung \(\ x^2 y^2 + x^2 z^2+ y^2 z^2 − xyz = 0\ \) beschrieben werden kann (Fläche 4. Ordnung).
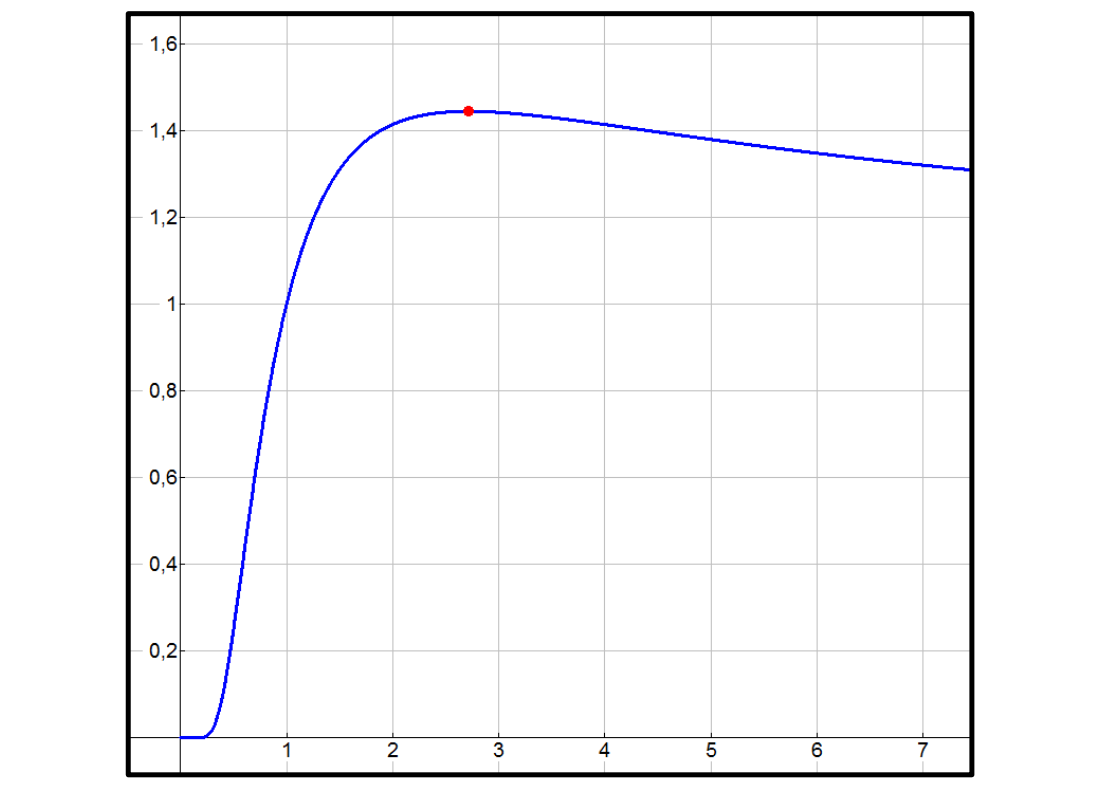
Manchmal findet man unter der Bezeichnung Steiner-Problem die Aufgabe, das Maximum der Funktion f mit \(\ f(x)=\sqrt[x]{x}\ \) zu bestimmen. Dieses liegt an der Stelle \(x =\ \)e.







Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.