Ghyath-al-Din Jamshid al-Kashi gilt als der letzte große Mathematiker des islamischen Mittelalters. Geboren in Kashan (im heutigen Iran), erlebt er als Kind die Eroberung der Region durch mongolische Heere unter dem Regenten Timur. Erst nach dessen Tod im Jahr 1405 und der Teilung des Reiches erblüht das kulturelle und wissenschaftliche Leben wieder. Der Thronfolger Timurs, Shak Rokh, ernennt seinen Sohn Ulugh Beg (1394–1449), der Name bedeutet »Großprinz«, zum neuen Herrscher der Hauptstadt des Landes, Samarkand (heute in Usbekistan).

Erste Berichte über al-Kashi stammen aus dem Jahr 1406: Er arbeitet in der Umgebung von Kashan als Astronom und Mathematiker und beobachtet 1406 eine Mondfinsternis; kurze Zeit danach beendet er ein Werk über die Größe des Kosmos, in dem er sich kritisch mit den Überlegungen seiner Vorgänger auseinandersetzt. 1414 veröffentlicht er die korrigierte und erweiterte Fassung der großen astronomischen Tafeln des Nasir al-Din al-Tusi (1201–1274), die er – wie es üblich ist – dem Herrscher widmet. Die »Tafeln des Khan« (Khagani Zij) enthalten – neben umfangreichen trigonometrischen Tabellen – einen Sternenkatalog sowie Angaben über die Bewegungen der Sonne, des Mondes und der Planeten – beschrieben durch Äquatorialkoordinaten (Koordinatensystem, das durch die Äquatorebene und die Polachse gegeben ist) und auch durch Ekliptikalkoordinaten.

1416 folgt eine Abhandlung über astronomische Instrumente, darunter sind auch Erfindungen al-Kashis, zum Beispiel ein Gerät zur Vorhersage von Planeten-Konjunktionen.

Um 1420 dann lädt Ulugh Beg die sechzig besten Wissenschaftler des Landes ein, als Forscher und Lehrer an die neu gegründete Hochschule (arabisch: Madrasa) nach Samarkand zu kommen; al-Kashi ist sicherlich der Fähigste von ihnen. Später wird man ihn als den zweiten Ptolemäus bezeichnen.

Aus Briefen, die al-Kashi an seinen Vater schreibt und die erhalten sind, weiß man, dass al-Kashi und sein Herrscher Ulugh Beg sich mit großem gegenseitigem Respekt begegnen; denn Ulugh Beg ist ebenfalls ein hervorragender Astronom. Im Jahr 1424 beginnt dieser mit dem Bau des großen Observatoriums in Samarkand, dessen Fertigstellung im Jahr 1437 al-Kashi nicht mehr erlebt. Dass die Astronomie in islamischen Ländern eine neue Blüte erlebt, hängt mit der Notwendigkeit präziser Beobachtungen und geometrischer Berechnungen zusammen, die sich aus religiösen Anweisungen ergeben, zum Beispiel die Bestimmung der Mekka-Richtung oder des Beginns eines islamischen Monats (Augenblick, in dem die Mondsichel nach Neumond zum ersten Mal sichtbar ist).

1424 und 1427 erscheinen zwei Werke al-Kashis, die zu den bedeutendsten in der Geschichte der arabisch-islamischen Mathematik gehören: die »Abhandlung über den Kreisumfang« sowie der »Schlüssel zur Arithmetik«, ein Kompendium der Mathematik, das an persischen Schulen noch bis ins 17. Jahrhundert als Lehrbuch verwendet wird.

In der »Abhandlung über den Kreisumfang« verfolgt al-Kashi das ehrgeizige Ziel \(\pi\) so genau zu bestimmen, dass der auftretende Fehler bei einem Kreis von der Ausdehnung der Himmelskugel (damalige Schätzung: 600 000 Erddurchmesser) kleiner sein soll als die »Breite eines Pferdehaars« (alte Maßeinheit, entspricht 0,7 mm). Die Berechnungen führt er im Sexagesimalsystem an einem regelmäßigen Vieleck mit \(805\ 306\ 368 = 3 \cdot 228\) Ecken durch, mit zehnstelliger Genauigkeit (umgerechnet 16-stellige Genauigkeit im Dezimalsystem), und übertrifft damit alle bis dahin durchgeführten Berechnungen, zum Beispiel die von Zu Chongzhi aus dem fünften Jahrhundert.

Der »Schlüssel zur Arithmetik« ist als Lehrwerk für Studenten geschrieben; das Buch soll künftigen Astronomen, Vermessern, Architekten, Buchhaltern und Händlern die notwendigen Kenntnisse der Mathematik vermitteln.

Al-Kashi beschäftigt sich im ersten Teil des Werkes mit dem Rechnen mit natürlichen Zahlen (unter Verwendung der aus Indien eingeführten Ziffernschreibweise), im zweiten Teil mit dem Rechnen mit Brüchen im Sexagesimal-System, so wie dies im arabisch-islamischen Kulturraum damals üblich ist, aber auch mit Brüchen im Dezimalsystem, die in Europa erst 150 Jahre später von Simon Stevin (1548–1620) wieder entdeckt werden.

Dass auch Brüche im 60er-System notiert werden, hängt mit dem Rechnen mit Winkelgrößen und Zeiten zusammen \((1° = 60'; 1' = 60'', 1 h = 60 min)\); sogar die damals verwendete Währung enthält diese 60er-Unterteilung (1 Dirham = 60 Fulus).

Zu den Rechenarten, die in dem Buch behandelt werden, gehört auch das schriftliche Wurzelziehen. Al-Kashi führt das Ziehen der fünften Wurzel aus 44.240.899.506.197 vor – unter Verwendung des binomischen Lehrsatzes und der Binomialkoeffizienten – und erhält 536 + 21/414.237.740.281, wobei er den Bruchteil durch lineare Interpolation berechnet \((537^5 – 536^5 = 414.237.740.281)\).

Die anderen Teile des Werkes beschäftigen sich mit der Berechnung von Flächen und Volumina, unter anderem von regulären und halbregulären Polyedern (platonischen und archimedischen Körpern) sowie von anderen, in der islamischen Architektur verwendeten Formen (Kuppeln), mit dem Problem der Irrationalität von Zahlen, mit der Summation von endlichen Zahlenfolgen sowie mit Problemen aus der Zahlentheorie. In Frankreich wird heute noch ein Satz als »Le théorème d'al-Kashi« bezeichnet, der bei uns unter dem Namen Kosinussatz geführt wird, denn al-Kashi ist der Erste, der erläutert, wie der (bereits anderen arabisch-islamischen Mathematikern bekannte) Satz bei der Triangulation (Vermessung von Dreiecken) angewendet werden kann.

Das letzte Meisterwerk al-Kashis ist »Die Abhandlung über Sehne und Sinus« aus dem Jahr 1427, in dem ihm die Berechnung eines sehr genauen Wertes für sin(1°) gelingt, aus dem dann Ulugh Beg später Näherungswerte für andere Winkel ableitet:

Aus der Kenntnis von \(\sin (30°)=\frac{1}{2},\) \(\cos(30°)=\frac{\sqrt{3}}{2}\) (im gleichseitigen Dreieck) und \(\cos(36°)=\frac{\sqrt{5} +1}{4},\) \(\sin(36°)= \frac{\sqrt{10–2\sqrt{5}}}{4}\) (im regulären 10-Eck) bestimmt er mithilfe der Additionstheoreme genaue Werte von \(\sin(6°) = \sin(36°-30°)\) und \(\cos(6°),\) hieraus dann mithilfe von \(\sin(3°)=\sqrt{ \frac{1-\cos(6°)}{2}},\) \(\cos(3°)=\sqrt{ \frac{1+\cos(6°)}{2}}\) Näherungswerte für \(\sin(3°)\) und \(\cos(3°).\) Um auf \(\sin(1°)\) beziehungsweise \(\cos(1°)\) schließen zu können, verwendet er schließlich noch die von ihm entdeckten Dreifachwinkelformen:
\(\sin(3\alpha) = \cdot \sin(\alpha) – 4\cdot \sin^3(\alpha)\) und \(\cos(3\alpha) = 4\cdot \cos^3(\alpha) – 3 \cdot \cos(\alpha).\) Al-Kashi interpretiert die Formeln dahingehend, dass für die Dreiteilung des Winkels von 3° eine kubische Gleichung zu lösen ist:
\(x^3 + b = a \cdot x,\) wobei \(x = \sin(1°); a =\frac{3}{4} ; b = \frac{1}{4} \cdot \sin(3°)\). Diese Lösung bestimmt er iterativ: \(x=\frac{b+x^3}{a}\approx\frac{b}{a}\) ist eine erste Näherungslösung, die man wieder in die Gleichung einsetzt: \(x_2=\frac{b+x_1^3}{3}\), dann \(x_3=\frac{b+x_2^3}{a}\) und so weiter.

Schließlich erhält Al-Kashi ein auf 18 Dezimalstellen genaues Ergebnis: \(sin(1°) = 0,017452406437283571\)

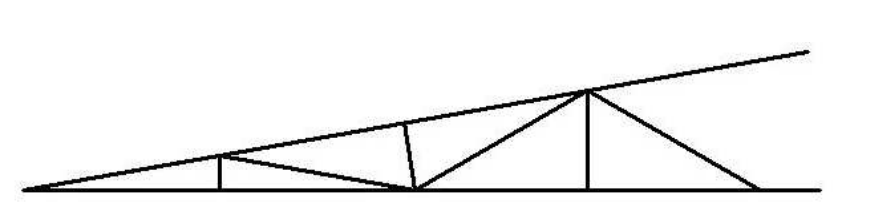
Die erwähnten Dreifachwinkelformen lassen sich aus der unten abgebildeten Figur herleiten: