Wittenbauer
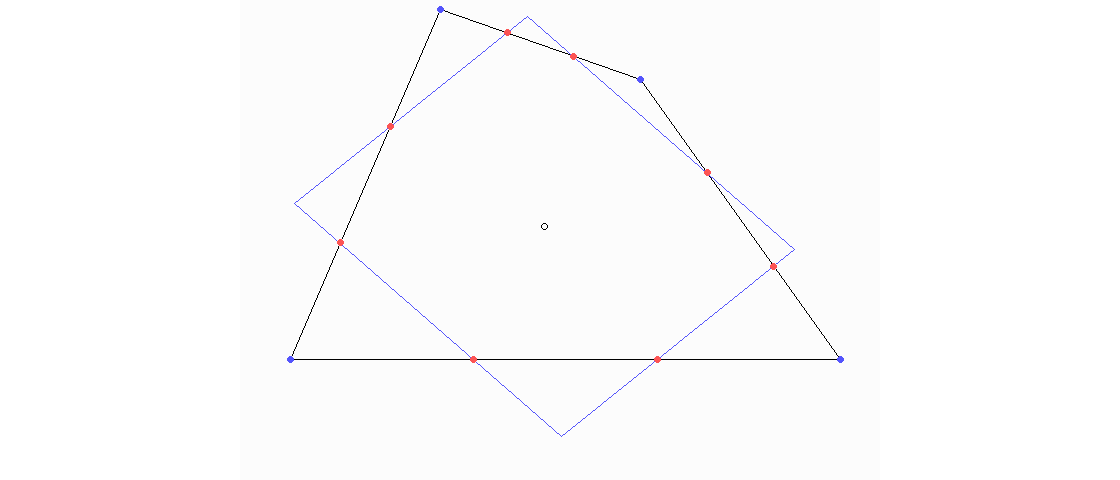
Wenn man die Seiten eines konvexen ebenen Vierecks (schwarz) drittelt, kann man mit 4 Geraden (blau) "die Ecken abschneiden" und bekommt ein Parallelogramm.
Können Sie zeigen, dass der Mittelpunkt dieses Parallelogramms der Schwerpunkt der Fläche des ursprünglichen Vierecks ist (Satz von Wittenbauer)?
Die Diagonalen zerlegen das Viereck auf zwei Arten in zwei Dreiecke, und es gibt einige Parallelen zu ihnen.

Die schwarz markierten Punkte sind die Mittelpunkte der roten Strecken und damit Schwerpunkte von je einer "Hälfte" des Vierecks (das heißt von je einem Dreieck aus 3 der 4 Ecken des Vierecks, das durch eine grüne Strecke begrenzt ist).
Die beiden eingezeichneten Verbindungsstrecken zwischen den schwarzen Punkten schneiden sich im (Flächen-)Schwerpunkt des ganzen Vierecks, und sie liegen auf Mittelparallelen des blauen Parallelogramms, ihr Schnittpunkt ist also dessen Mittelpunkt. Diesen Satz verdanken wir Ferdinand Wittenbauer (1857–1922), der an der Technischen Hochschule Graz wirkte und dort die grafische Dynamik, ein Teilgebiet der Technischen Mechanik, begründete.
Dass das Parallelogramm wirklich eines ist, folgt daraus, dass seine Seiten parallel zu den grünen Diagonalen des gegebenen Vierecks sind. Das gilt nicht nur für Drittelungen der Seiten, sondern für jede symmetrische Teilung. Besonders bekannt ist der Fall mit den Seitenmitten. Dann hat man den Spezialfall von Varignon (siehe dazu das Rätsel "Varignon"), in dem die Parallelogrammseiten halb so lang wie die Diagonalen des Vierecks sind. Der Mittelpunkt des Varignon-Parallelogramms ist der Eckenschwerpunkt des gegebenen Vierecks. Aber warum?
Die Seitenmitten sind Schwerpunkte von je zwei benachbarten (allesamt gleich schweren!) Ecken, die Bimediane halbieren sich also gegenseitig im Schwerpunkt von allen vieren.
Die Schwerpunkte der Ecken und der Fläche des Vierecks sind also im Allgemeinen verschieden, anders als beim Dreieck, wo man sie oft gar nicht deutlich unterscheidet.
Bei welchen Vierecken fallen Ecken- und Flächenschwerpunkt zusammen?
Im Falle der Punktsymmetrie, also beim Parallelogramm.



Schreiben Sie uns!
Beitrag schreiben