Quadrate um ein Dreieck
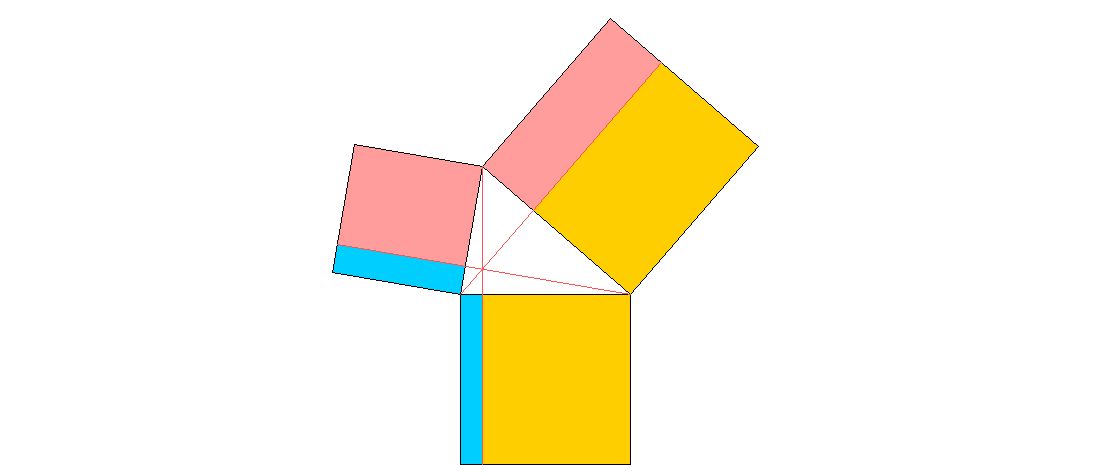
Eine Verallgemeinerung des pythagoreischen Flächensatzes auf spitzwinklige Dreiecke sagt, dass die Rechtecke, die man durch Zerlegen der angefügten Quadrate entlang der verlängerten Höhen des Dreiecks erhält, paarweise flächengleich sind, wie hier durch gleiche Farben angezeigt ist. Wie können Sie diese Aussage beweisen?
Betrachten Sie einander ähnliche rechtwinklige Teildreiecke.
Die beiden grün schraffierten rechtwinkligen Dreiecke sind zueinander ähnlich, da ihre drei Winkel übereinstimmen. Somit verhalten sich die Seiten des Ausgangs-Dreiecks umgekehrt wie die (hier der oberen Ecke zugewandten) Abschnitte auf ihnen: Die beiden roten Rechtecke sind also flächengleich. Entsprechendes gilt für die anderen beiden Flächenpaare.
Was ergibt das für den Grenzfall eines rechtwinkligen Dreiecks?
Die Kathetenquadrate werden gar nicht zerlegt, und das Hypotenusenquadrat gliedert sich in zwei Rechtecke, die zu je einem Kathetenquadrat flächengleich sind. Es folgt der Kathetensatz und direkt daraus der pythagoreische Satz.
Zurück zum spitzwinkligen Dreieck: Für die Verallgemeinerung des pythagoreischen Satzes gab es doch auch eine algebraische Ausdrucksweise: nicht nur \(c^2=a^2+b^2\), sondern …?
Es ist der Kosinus-Satz der ebenen Trigonometrie: \(c^2=a^2+b^2-2ab \cos\gamma\). Man kann ihn ziemlich einfach aus unserem Bild ablesen. Natürlich gibt es ihn in drei Versionen, eine für jeden der spitzen Winkel. Wendet man ihn auf den rechten Winkel des rechtwinkligen Spezialfalls (\(\cos \gamma=0\)) an, gibt es natürlich wieder den pythagoreischen Satz.
Schreiben Sie uns!
Beitrag schreiben