Im Jahr 1893 gelangte der russische Ägyptologe Wladimir Golenischtschew in den Besitz eines fast 4000 Jahre alten Papyrus mit mathematischem Inhalt. Dieser enthält 25 Rechenaufgaben, und eine davon lautet: »Form der Berechnung eines Haufens, gerechnet anderthalbmal zusammen mit vier. Er ist gekommen bis zehn. Der Haufe nun nennt sich?«

Im Original ist der Text natürlich in ägyptischer hieratischer Schrift verfasst, die deutsche Übersetzung stammt aus dem Jahr 1930, und mit »Haufen« oder »Hau« (in moderner Übersetzung »Aha« transkribiert) ist eine unbekannte Größe gemeint. Man muss ein wenig nachdenken, um zu verstehen, was da gemeint ist. Mit den heute verwendeten Symbolen wird das Problem aber leicht klar. Die Aufgabe lautet:

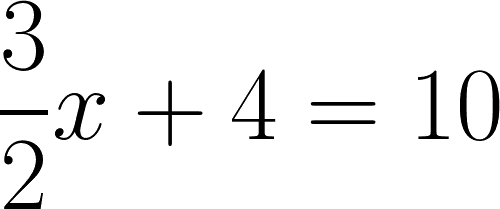
Der Moskauer Papyrus gibt auch gleich den Weg zur Lösung an. Zuerst heißt es dort: »Berechne du die Größe dieser 10 über dieser 4. Es entsteht 6.« Das meint nichts anderes als das, was wir auch tun würden, um die Gleichung zu lösen. Nämlich die 4 von der linken Seite des Gleichheitszeichens auf die rechte zu bringen, also 4 von 10 abzuziehen, so dass 6 stehen bleibt. Dann erklärt uns die ägyptische Mathematik: »Rechne du mit anderthalb, um zu finden 1. Es entsteht 2/3.« Wir sollen also aus den »anderthalb« 1 machen, und das geht, in dem wir mit 2/3 multiplizieren. Bei der modernen Methode zur Lösung machen wir das natürlich auf beiden Seiten der Gleichung gleichzeitig und erhalten sofort das Ergebnis »x = 4«.

Im Papyrus ist das noch einmal extra aufgeführt: »Berechne du 2/3 von diesen 6. Es entsteht 4. Siehe: 4 nennt sich. Du hast richtig gefunden.« Das Rechnen mit Unbekannten hat schon immer zum Fundament der Mathematik gehört. Wir benutzen dazu heute die Methoden der modernen Algebra. Sie geht auf die Arbeit der europäischen »Cossisten« (nach »Coß«, dem mittelalterlichen Ausdruck für das Unbekannte in der Mathematik) zurück, die im 16. Jahrhundert anfingen, Rechenregeln zu veröffentlichen, mit denen sich Gleichungen symbolisch manipulieren lassen. Bis dann aber auch eine einheitliche Notation mit überall gleich verwendeten Symbolen entstand, dauerte es noch bis ins 18. Jahrhundert. Ohne diese Entwicklung wäre die moderne Mathematik mit all ihren wichtigen Erkenntnissen nicht möglich gewesen. Mit dem, was in alten ägyptischen Texten beschrieben wird, kann man zwar sehr gut praktische Probleme lösen. Doch die Textaufgaben mit ihren umständlichen Beschreibungen der Rechenschritte lassen sich nur schwer verallgemeinern. Ihnen fehlt die Möglichkeit zur Abstraktion – aber genau das ist es, was die Mathematik eigentlich ausmacht.

Wenn man ein mathematisches Problem von seinem konkreten Kontext löst und es mit abstrakten Symbolen und Zeichen beschreibt, dann steht die Gleichung auf einmal für sich selbst. Sie muss sich nicht mehr auf ein Problem der realen Welt beziehen, sondern beschreibt nur noch einen Zusammenhang zwischen abstrakten Größen. Daraus kann man neue Eigenschaften dieser Größen ableiten und neue Zusammenhänge finden, die dann – wenn auch nicht zwingend – wieder auf Probleme der realen Welt angewandt werden können.

Je abstrakter die mathematische Sprache geworden ist, desto wertvoller wurde sie auch. Man muss sich nun zwar mehr anstrengen, um sie zu verstehen. Aber es lohnt sich!