Als Astronom kenne ich Johannes Kepler natürlich hauptsächlich wegen seiner astronomischen Arbeit über die Bewegung der Planeten im Sonnensystem. Aber Kepler hat sich noch mit vielen anderen Dingen beschäftigt. Er konstruierte beispielsweise eine Pumpe zur Entwässerung von Bergwerksstollen, entwickelte eine Formel zur Berechnung des Volumens von Weinfässern und verfasste mit "Somnium" eine der ersten Sciencefiction-Erzählungen. Und im Jahr 1611 schrieb er ein Werk mit dem Titel "Über die sechseckige Schneeflocke". Ausgehend von der Untersuchung der Kräfte, die das regelmäßige Wachstum von Schneeflocken bestimmen, gelangte Kepler zur Berechnung der maximalen Dichte von Kugelpackungen.

Der englische Mathematiker und Astronom Thomas Harriot hatte sich Gedanken darüber gemacht, wie man Kanonenkugeln am besten auf Schiffen verstauen könnte, und diskutierte mit seinem Freund Kepler dieses Problem. Heute, in einer Zeit, in der Kanonenkugeln eher keine große Rolle im Leben der Menschen mehr spielen, kann man sich das Problem mit einer anderen Situation besser vorstellen: Wie kann man Orangen (oder anderes rundes Obst) so stapeln, dass sie ein vorgegebenes Volumen möglichst gut ausfüllen?

Wirft man eine Menge gleich großer Kugeln einfach zufällig in eine Kiste, dann wird diese zu ungefähr 65 Prozent gefüllt – entsprechende Experimente hat man tatsächlich angestellt. Aber Johannes Kepler fand Anordnungen, die seiner Meinung nach noch besser waren. Man beginnt damit, die Kugeln in der untersten Lage in Form eines hexagonalen Gitters anzuordnen. Die Kugeln der zweiten Lage werden dann in die tiefsten Punkte der ersten Lage gelegt und so weiter. Diese Art, runde Objekte zu stapeln, ist jene, die alle Obsthändler ganz intuitiv anwenden, wenn sie zum Beispiel aus Orangen eine Pyramide errichten – und Kepler war der Meinung, dass sie auch die optimale ist:

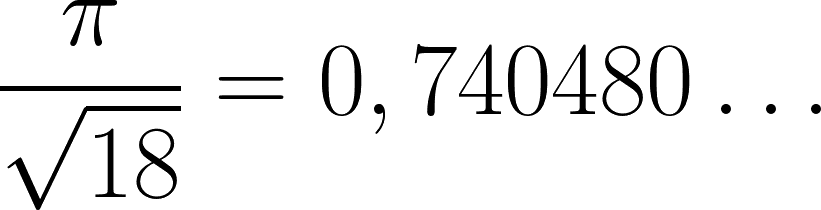
Diese Zahl ist das Resultat von Keplers Berechnungen – stapelt man die Kugeln in der von ihm beschriebenen Art und Weise, dann füllen sie das Volumen zu 74,0480... Prozent aus. Und er vermutete, dass dies auch die maximal erreichbare Dichte sei. Es gäbe keine andere Möglichkeit, die Kugeln zu stapeln, um eine noch höhere Dichte zu erreichen.

Mathematisch beweisen konnte Kepler diese Behauptung aber nicht, weswegen sie als keplersche Vermutung bezeichnet wurde – die fast 400 Jahre lang auch so bezeichnet werden musste. Denn trotz der eigentlich simplen Aufgabenstellung und der zahlreichen Versuche, die Vermutung zu beweisen, scheiterten die Mathematiker immer wieder daran.

Erst 1998 konnte der Amerikaner Thomas Hales einen Beweis vorlegen. Seine Methode ist allerdings bis heute umstritten. Hales konnte Keplers Vermutung in viele, aber nicht unendlich viele Fälle aufspalten und machte sich daran, all diese Anordnungen im Laufe von mehreren Jahren per Computer zu überprüfen. Der endgültige Beweis bestand aus mehr als 250 Seiten an Aufzeichnungen und drei Gigabyte an Computerdaten. Die Gutachter der Zeitschrift "Annals of Mathematics" prüften Hales' Arbeit vier Jahre lang und gaben danach bekannt, sie wären zu 99 Prozent sicher, dass der Beweis richtig wäre. Sie könnten aber nicht mit letzter Gewissheit bestätigen, dass alle vom Computer durchgeführten numerischen Berechnungen korrekt wären.

In der Mathematik zählt aber nur die absolute Gewissheit. Hales arbeitet deswegen seit 2003 daran, einen formal vollständigen Beweis der keplerschen Vermutung zu erstellen. Dazu übersetzt er seine Ausführungen in eine abstrakte Programmiersprache, deren logische Aussagen von Computerprogrammen überprüft werden können. Ob die menschlichen Mathematiker aber dann der Logik des Computers vertrauen und den neuen Beweis akzeptieren, bleibt abzuwarten.