Beim "Küssen" geht es um die Geometrie und mathematische Ausdrücke, die auf den ersten Blick wenig Romantik aufkommen lassen:

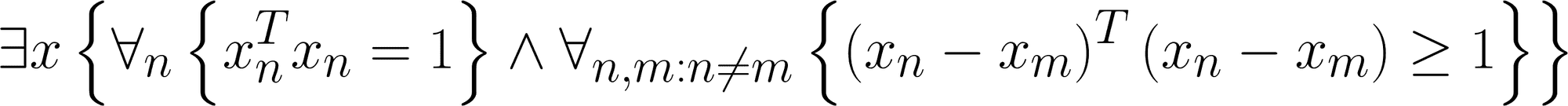
Mit dieser langen Kette an Symbolen beschreibt man eine spezielle Konfiguration von Sphären. In normale Sprache übersetzt, handelt es sich um die Anzahl an Kugeln, die man so um eine zentrale Kugel herum positionieren kann, damit diese von allen Kugeln berührt wird, ohne dass die Kugeln sich dabei durchdringen. Oder, noch ein wenig mehr am Alltag orientiert, um die Frage: Wie viele weiße Billardkugeln kann man so um eine schwarze Billardkugel herum anordnen, damit jede weiße Kugel die schwarze immer berührt?

Diese Frage stellten sich schon 1692 der berühmte Naturwissenschaftler Isaac Newton und sein nicht ganz so berühmter Kollege David Gregory. Newton war der Meinung, man könne höchstens 12 Kugeln so positionieren, damit sie die zentrale Kugel "küssen". Gregory widersprach und meinte, es ließe sich noch eine dreizehnte Kugel irgendwo dazwischenquetschen. Probiert man das Ganze praktisch aus, dann erscheint Gregorys Vermutung plausibel. Zwischen den zwölf Kugeln ist noch erstaunlich viel Platz. Man kann sogar zwei beliebige der zwölf Kugeln so verschieben, dass sie ihre Plätze tauschen, ohne dabei jemals den Kontakt zur zentralen Kugel zu verlieren.

Man hat das Gefühl, dass da irgendwo noch eine dreizehnte Kugel dazwischenpassen muss. Tut sie aber nicht – auch wenn es bis zur Mitte des 20. Jahrhunderts gedauert hat, um das auch mathematisch formal beweisen zu können. Die "Kusszahl" beträgt für diesen Fall 12, und Newton hatte (wie so oft) Recht.

Der oben angeführte mathematische Ausdruck ist aber unter anderem auch deshalb so komplex, weil er das Problem der Kusszahlen viel allgemeiner formuliert als im Beispiel mit den Billardkugeln. Es geht um die Frage nach der maximalen Anzahl n-dimensionaler Einheitskugeln, die gleichzeitig eine weitere n-dimensionale Einheitskugel im euklidischen Raum berühren können, ohne dass es zu Überschneidungen kommt. Im uns vertrauten dreidimensionalen Raum ist die Einheitskugel nichts anderes als eine Kugel mit dem Radius 1. "Einheitskugeln" kann man aber auch problemlos für den zweidimensionalen Fall definieren: Das ist dann einfach nur ein Kreis mit dem Radius 1, und es ist leicht zu sehen, dass man genau sechs andere Kreise um einen zentralen Kreis positionieren kann, so dass dieser von allen berührt wird. Im eindimensionalen Fall ist eine "Einheitskugel" nur eine Linie – offensichtlich können hier nur zwei weitere Linien die zentrale Linie (links und rechts) berühren.

Im 3-D-Raum ist die Kusszahl also 12, in zwei Dimensionen beträgt sie 6, und im eindimensionalen Fall ist sie gleich 2. Es hindert uns aber nichts, die Frage nach den sich küssenden Einheitskugeln auch für vier, fünf oder noch mehr Dimensionen zu stellen. Vorstellen können wir uns diese hochdimensionalen Räume zwar nicht mehr anschaulich, aber mathematisch rechnen kann man dort genauso. Es wird, zumindest bei der Frage nach der Kusszahl, jedoch sehr schnell sehr schwierig.

Es hat bis zum Jahr 2003 gedauert, bevor der russische Mathematiker Oleg Musin beweisen konnte, dass die Kusszahl in vier Dimensionen gleich 24 ist. Außerdem kennt man noch die Kusszahl für 8 Dimensionen (sie beträgt 240) und weiß, dass man im 24-dimensionalen Raum ganze 196 560 Einheitskugeln mit 24 Dimensionen gleichzeitig eine zentrale Kugel küssen lassen kann.