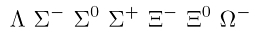Die Hyperonen sind eine Klasse besonders schwerer Baryonen, von denen man in der Teilchenphysik sieben kennt. Alle Hyperonen sind seltsame Teilchen, also Teilchen mit der QuantenzahlSeltsamkeit (engl. Strangeness) verschieden von null. Man kann leicht ihre Seltsamkeit herausfinden, indem man für jedes im Hyperon enthaltene strange-Quark jeweils S = -1 rechnet und für jedes strange-Antiquark S = +1 hinzuaddiert. Die Summe aller Seltsamkeiten ergibt die resultierende Seltsamkeit des Hyperons.

7 Hyperonen in aufsteigender Masse

• Das Lambda-Hyperon mit einer Masse von 1115.683 MeV, Quarkgehalt uds (daher elektrisch neutral), Spin 1/2, Strangeness ('Gehalt an Strange-Quarks') -1 und einem Isospin von I = 0. Es handelt sich also um ein Isospinsingulett, also wegen 2I+1=1, einem Teilchen.
• Drei Sigma-Hyperonen mit zugehörigen Antiteilchen. Die Sigma-Hyperonen bilden ein Isospintriplett (I = 1). Alle haben Strangeness -1 und Spin 1/2. Das negativ geladene Sigma-Hyperon hat eine Masse von 1197.449 MeV, Quarkgehalt dds. Das neutrale Sigma-Hyperon hat eine Masse von 1192.642 MeV, Quarkgehalt uds. Das positiv geladene Sigma-Hyperon hat schließlich eine Masse von 1189.37 MeV und Quarkgehalt uus.
• Zwei Xi-Hyperonen mit jeweiligen Antiteilchen. Sie bilden ein Isospindublett (I = 1/2). Beide haben Strangeness -2 und Spin 1/2. Das negative Xi-Hyperon hat eine Masse von 1321.31 MeV und Quarkgehalt dss, während das neutrale Xi-Hyperon Masse von 1314.83 MeV und Quarkgehalt uss hat.
• Das schwerste Hyperon ist das Omega-Hyperon, das negativ geladen ist und ein Isospinsingulett ist (I = 0). Das Omega-Hyperon hat eine Masse von 1672.45 MeV und ist damit fast 1.8fach schwerer als das Proton. Die Strangeness ist unter den Hyperonen mit einem Wert von -3 ebenfalls am höchsten. Der Spin beträgt 3/2 und Quarkgehalt sss.
  (Datenquelle:Particle Physics Booklet, Stand Juli 2002)

Wo gibt's denn sowas?

Unter normalen, irdischen Bedingungen findet man keine Hyperonen. Sie bilden sich erst bei sehr hohen Teilchendichten, die vergleichbar sind mit der Kernmateriedichte, die bei 2.5 × 10¹⁴ g cm^-3 liegt. So spielen die Hyperonen im Innern von Neutronensternen und Quarksternen eine Rolle, wenn eine kritische Übergangsdichte von etwa zwei- bis dreifacher Kernmateriedichte überschritten wird: dann setzt die Hyperonisierung ein und stellt einen Beitrag zur Zustandsgleichung dieser ultradichten Materie. Die Kernphysiker umschreiben das so: Die Materie erhält hyperonische Freiheitsgrade.