Der Spin wird im Deutschen mit dem Begriff Eigendrehimpuls bezeichnet. Spin ist ebenso wie Ladung und Masse eine fundamentale Eigenschaft eines Teilchens und stellt einen weiteren Freiheitsgrad dar. Allerdings besitzt er als quantenmechanische Observable kein klassisches Analogon. Die Vorstellung, dass ein kugelförmiges Teilchen um seine eigene Achse rotiert ist nur eine klassische Vorstellung, die nicht besonders hilfreich ist. Neben anderen Quantenzahlen ist die SpinquantenzahlS ist eine unveränderliche Teilcheneigenschaft.

Dirac-Theorie: Spin ist relativistisch

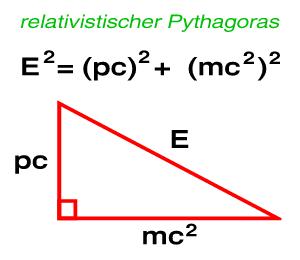
Der Spin ist eine relativistische Eigenschaft! Man kann ihn physikalisch nur erklären, wenn man die Konzepte der Quantenmechanik mit der Speziellen Relativitätstheorie verknüpft. Die fundamentalen Gleichungen dieser Dirac-Theorie, benannt nach dem britischen Physiker Paul Dirac (1902 – 1984), kann man recht schnell ableiten, wenn man die Größen E und p im relativistischen Energiesatz ('relativistischer Pythagoras', siehe Abbildung rechts) gemäß des Korrespondenzprinzips in Differentialoperatoren (E: Zeitableitung, p: Ortsableitung) übersetzt. Die resultierende Gleichung nennt man Klein-Gordon-Gleichung, die die Bewegungsgleichung des Elektrons ist. Sie ist zweiter Ordnung in der Ableitung nach Ort und Zeit und eine Wellengleichung.
Diracs Verdienst war es nun, diese Gleichung zu faktorisieren, so dass die Dirac-Gleichung resultierte. Mit dieser Gleichung kann man das Elektron (bzw. dessen Antiteilchen, das Positron) als freies Teilchen oder im elektromagnetischen Feld beschreiben. Bei der Linearisierungsprozedur tauchten neue Objekte auf, quadratische Matrizen, die man Dirac-Matrizen (oder auch Spinoperatoren) nennt. Sie genügen bestimmten Kommutatorrelationen (Vertauschungsrelationen). Dirac folgerte, dass nun im Allgemeinen auch die Wellenfunktionen nicht mehr einkomponentige Objekte sein können: man notiert sie wie einen Vektor und nennt sie Spinor. In diesen Komponenten steckt die ganze Information über den Teilchenspin. Die Dirac-Gleichung ist also eine Matrix-Gleichung und durch die Linearisierung nur noch erster Ordnung in Zeit und Ort.

Antimaterie

Eine bahnbrechende Erkenntnis bei der Formulierung der Dirac-Gleichung war die Vorhersage des Positrons, des Antiteilchens des Elektrons mit gleicher Ruhemasse (511 keV), aber positiver Ladung. Diese Leistung gelang durch eine physikalische Interpretation einer zweiten Lösung der Dirac-Gleichung. Der Begriff Antimaterie war mit dieser theoretischen Leistung geboren.
Im speziellen Fall der Elektronen und Positronen konstituieren sich die Dirac-Matrizen aus den Pauli-Matrizen. Die Pauli-Matrizen sind 2 × 2-Matrizen, während die Dirac-Matrizen 4 × 4-Matrizen sind. Die Wellenfunktionen des Elektrons/Positrons sind in der Dirac-Theorie vierkomponentige Spinoren.

Hilbertraum des Spins

Betrachtet man nur den Hilbertraum des Spins, so gilt allgemein, dass ein Teilchen mit Spinquantenzahl S als (2S+1)-komponentiger Spinor geschrieben werden kann. Elektronen, Positronen, Protonen und Neutronen haben Teilchenspin 1/2, so dass ihr Hilbertraum des Spins zweidimensional ist und ihre Spinoren zwei Komponenten haben: 'Spin nach oben' (engl. spin up) und 'Spin nach unten' (engl. spin down). Diese Orientierungen sind so zu verstehen, dass der Spinvektor S parallel oder antiparallel zur z-Achse ausgerichtet sein kann. Diese Eigenschaft nennen Quantenphysiker generell Richtungsquantelung, d.h. es kann nur diskrete Einstellungsmöglichkeiten des Spins relativ zur z-Achse geben. Dies kann man als Eigenwertgleichung für den Spinoperator S_z (der Projektion des Spinoperators S auf die z-Achse) darstellen, wobei die diskreten Eigenwerte gerade die Produkte aus Planckschem Wirkungsquantum h geteilt durch 2π und der magnetischen Quantenzahl m sind. m kann bei einem Teilchenspin S die Werte -S, -S+1, -S+2....+S annehmen. Im Fall S = 1/2 sind das nur die beiden Werte m = -1/2 und m = +1/2.
Die Umstellung zwischen diesen beiden Werten, die auch verschiedenen energetischen Zuständen entsprechen, vermitteln Spinoperatoren, die den Spin umklappen können (engl. spin flip). Solche Leiter- oder Stufenoperatoren sind analog zu den Erzeugungs- und Vernichtungsoperatoren der Quantenfeldtheorien. In der Quantentheorie des Spins erzeugen bzw. vernichten sie Spinquanten.

Terminologie bei Spins

• Teilchen mit S = 0 nennt man skalare Bosonen. Dazu gehören beispielsweise das Higgs-Teilchen und die Phononen. Letztere sind quantisierte Gitterschwingungen im Festkörper.
• Teilchen mit S = 1 nennt man Vektorbosonen. Hier seien die Photonen, die Gluonen der QCD, die schwachen Eichbosonen W^-, W⁺ und Z⁰ der schwachen Wechselwirkung, die X-Bosonen und Y-Bosonen der GUT sowie das Magnon als Beispiele genannt.
• Teilchen mit S = 2 nennt man Tensorbosonen. Diese Eigenschaften ordnen die Physiker dem hypothetischen Graviton zu, das die Gravitation als Eichboson vermitteln soll.

Bedeutung des Spins

Der Spin spielt eine zentrale Rolle im Aufbau der Materie: so ist das Periodensystem der Elemente nur dann verständlich, wenn man den Elektronenspin berücksichtigt. Die Natur unterscheidet Teilchen mit halbzahligem Spin, die Fermionen, von solchen mit ganzzahligem Spin, die Bosonen (siehe auch Spin-Statistik-Theorem). Diese beiden Teilchenarten verhalten sich unterschiedlich, weil die Fermionen dem Pauli-Prinzip unterliegen und nicht in allen Quantenzahlen übereinstimmen dürfen, d.h. nicht denselben quantenmechanischen Zustand besetzen dürfen. Für Bosonen gilt das nicht! Aus diesem Grund können sie alle denselben, den niedrigsten, energetischen Zustand einnehmen, wenn man das Bose-System nur weit genug abkühlt. Diese Phänomen kennt man als Bose-Einstein-Kondensation.
Der Magnetismus in Festkörpern ist ebenfalls eine Erscheinung, die nur mit dem Teilchenspin erklärt werden kann, also letztendlich auch ein relativistisches Phänomen! Magnetismus auf der subatomaren Ebene heißt, dass sich viele Spins spontan parallel orientieren. Gebiete im Festkörper gleicher Spin-Orientierung nennt man gerade die Weißschen Bezirke. Elektronen parallelen Spins versuchen einander auszuweichen, wie das Pauli-Prinzip diktiert. Die magnetischen Spinmomente etablieren dann eine spontane Magnetisierung des Festkörpers. In der theoretischen Festkörperphysik formuliert man dies mit den Hartree-Fock-Gleichungen, die Vielteilchensysteme quantentheoretisch beschreiben.

Drehimpulsalgebra

Die Rechtfertigung des Terminus Drehimpuls für den Spin besteht darin, dass er sich in einen speziellen, mathematischen Formalismus einbetten lässt, der Drehimpulsalgebra. Dahinter stecken bestimmte Kommutatorrelationen, die alle Drehimpulse erfüllen. Es sind Operatorgleichungen, die typisch sind für die Quantentheorie, und die bei Drehimpulsen eine wohldefinierte Form haben. Neben dem Spin als Eigendrehimpuls, erfüllt auch der klassische Bahndrehimpuls diese Relationen. Aber auch tiefer reichende Konzepte der Quantenfeldtheorien, wie der Isospin oder schwache Isospin transformieren sich wie Drehimpulse. Alle diese Spins sind als weitere Freiheitsgrade eines Quants aufzufassen und dienen deren Unterscheidung und Ordnung im Teilchenzoo der Elementarteilchenphysik.

Spins als Elementarmagneten

Mit jedem Spin ist ein magnetisches Moment verknüpft, über den spinbehaftete Teilchen an ein äußeres Magnetfeld koppeln können. So, wie sich ein Stabmagnet im irdischen Magnetfeld ausrichtet, richten sich Teilchen mit Spin in Magnetfelder aus. Mit einem spinbehafteten Teilchen verbindet sich die Vorstellung eines winzigen Elementarmagneten mit Nord- und Südpol. Im Stern-Gerlach-Versuch (1921) wird ein Atomstrahl (Silberatome) in ein starkes, inhomogenes Magnetfeld eingeschossen. Die Experimentatoren beobachten dann eine Aufspaltung des Strahls in zwei Teilstrahlen gleicher Intensität. Dieses Experiment deutete gerade auf eine bis dato verborgene Teilcheneigenschaft hin: den Spin. Die Aufspaltung demonstriert gerade die Richtungsquantelung.

Was passiert im Kernspintomographen?

Eine wichtige Anwendung des Teilchenspins in der Medizin ist die Kernspintomographie (Nuklearmagnetische Resonanz, kurz NMR). Hier nutzt man aus, dass auch die Teilchen im Atomkern, die Nukleonen (Neutronen und Protonen), halbzahligen Spin tragen. Alle diese Spins summiert man auf, um den Gesamtspin des Atomkerns, den Kernspin, zu erhalten. Bestimmte Atomkerne haben einen von null verschiedenen Kernspin (in der Medizin häufig H-1, H-2, C-13, N-14) und können als medizinische Diagnostika dienen. Der Kernspin koppelt an die Spins der Elektronen in der Atomschale und bewirkt auf diese Weise unterschiedliche energetische Zustände im Gesamtsystem. Man kann nun gezielt höhere energetische Zustände anregen, indem man das Material einem starken, homogenen Magnetfeld aussetzt, das von einem weiteren starken, inhomogenen Magnetfeld überlagert wird. Die Spins werden dann durch die Ausrichtung im Magnetfeld umgeklappt. Bestimmte Kerne lassen nur zwei Einstellungsmöglichkeiten zu: in Richtung des Magnetfeldes (parallel) oder entgegengesetzt dazu (antiparallel). Abschalten des Magnetfeldes lässt nun die Spins wieder in ihre Ruhelage zurückkehren (relaxieren): dieser Vorgang, eine Zustandsänderung von einem energetisch höheren in einen niederenergetischen Zustand ist mit der Emission eines Photons verbunden. In diesem Fall sind es Radiophotonen mit einigen MHz Strahlungsfrequenz. Diese Photonen sind das eigentliche Messsignal in der NMR und können mit einer photoempfindlichen Anordnung registriert werden. Das räumlich inhomogene Magnetfeld dient einer genauen Ortsauflösung des Signals, um die tomographischen Daten nach der Messung visualisieren zu können.

21cm-Linie in der Astronomie

In der Astronomie gibt es ebenfalls einen wesentlichen Beobachtungsindikator, der auf der Spin-Physik beruht: der Hyperfeinstrukturübergang im neutralen Wasserstoff (HI), der als 21cm-Linie im Radiobereich messbar ist. Dieser Übergang beruht auf den unterschiedlichen Einstellungsmöglichkeiten des Spins von Elektron und Proton (im Isotop H-1) zueinander: die Spinorientierungen können parallel oder antiparallel sein. Der antiparallele Zustand ist energetisch niedriger und der Grundzustand des atomaren Wasserstoffs. Wasserstoff ist das häufigste Element im Universum. Deshalb kommt es trotz hoher Lebensdauer von 1.1 × 10¹⁰ Jahre des energetisch angeregten Zustands zu einer signifikanten Emission von Photonen mit der zwischen diesen Energieniveaus korrespondierenden Frequenz von 1.42 GHz oder 21.1 cm Wellenlänge. Das interstellare Medium wird mit dieser Radiostrahlung weiträumig kartographiert und verrät damit die Verteilung des neutralen Wasserstoffs (21cm-Tomographie).