Die Gravitation (lat. gravitas: Schwere) ist eine der vier fundamentalen Kräfte in der Natur: die Schwerkraft.

Der Schwächling unter den Vieren

Diese Kraft ist von allen vier Grundkräften diejenige, die uns besonders vertraut ist. Die anderen Kräfte sind die elektromagnetische Kraft, starke und schwache Kraft – die beiden letztgenannten spielen eine besondere Rolle im subatomaren Bereich und sind wichtig, um den Zusammenhalt der uns umgebenden Materie zu verstehen.
Vergleicht man die Stärken der vier Fundamentalkräfte der Physik, z.B. mithilfe der Kopplungskonstanten, so wird klar, dass die Schwerkraft die schwächste aller Kräfte ist. Aufgrund dieser Tatsache kommt ein Dachziegel, der von einem Haus fällt, nicht bis zum Mittelpunkt der Erde, sondern zersplittert auf dem Erdboden: die elektromagnetischen Kräfte zwischen den Atomen des Ziegels und des Bodens haben für eine plötzliche Abstoßung gesorgt, eine Kraft, die die Gravitation nicht überwinden konnte. Noch stärker als der Elektromagnetismus ist die starke Kraft, der es sogar gelingt, elektrisch gleichartig geladene Protonen in einem Atomkern zusammenzuhalten. Der starken Kraft, aber auch der schwachen Kraft (Radioaktivität), verdanken wir also die Vielfalt der chemischen Elemente.

Der Schwächling dominiert

Doch das Attribut schwach ist nicht gleichbedeutend mit unwichtig: Die Gravitation ist die dominante Kraft auf der ganz großen Längenskala – sobald wir von Astronomischen Einheiten, Lichtjahren oder gar Milliarden Parsec sprechen. Denn Gravitation und elektromagnetische Kraft haben eine unendliche Reichweite! Doch die Schwerkraft hat im Gegensatz zum Elektromagnetismus die Eigenschaft, dass sie sich nicht abschirmen lässt. Die Konsequenz ist:

Gravitation dominiert das Universum.

Sie ist es, die die großräumigen Strukturen formt: Sie lässt die Planeten auf Ellipsenbahnen um die Sonne tanzen, sie komprimiert massereiche Sterne am Ende ihres Daseins zu Schwarzen Löchern, und sie bringt sogar Galaxien und Galaxienhaufen zum Verschmelzen.

Aber was ist eigentlich Gravitation?

So vertraut uns die Schwerkraft im Alltag ist, so rätselhaft ist sie auch. Es ist keinesfalls leicht zu verstehen, was die Natur der Gravitation ist. Selbst im 21. Jahrhundert wissen Physiker und Astronomen zwar viel über die Schwerkraft, aber auch heute noch sind wir weit davon entfernt, alles verstanden zu haben. Ist Gravitation überhaupt eine Kraft?
In den nächsten Abschnitten knöpfen wir uns fast 2400 Jahre menschlichen Denkens vor, das sich als bedeutsam für das Verständnis der Schwerkraft zeichnete. Das ist sicherlich ein wenig Aufwand, doch Gravitation ist ein wesentlicher Begriff der Physik und somit auch dieses Lexikons. Am Ende der Lektüre steht hoffentlich eine Ahnung von dem, was Gravitation überhaupt ist.

Antiker Vordenker: Aristoteles

Zu einem gut dokumentierten Pionier der Schwerkraftforschung muss man griechischen Gelehrten Aristoteles (384 – 322 v. Chr.) rechnen. Aristoteles ist eigentlich eher bekannt als bedeutender Geisteswissenschaftler, als Schüler Platons und als Erzieher Alexander des Großen. Aristoteles versuchte jedoch auch die Bewegung von Sonne, Mond und den damals bekannten Planeten durch recht einfache Modelle zu erklären. Die ruhende Erde war im Zentrum dieses Modells (geozentrisches Weltbild), und um sie kreisten Sonne, Mond und Planeten. Der Kreis als vollkommene, geometrische Figur stellte die Grundlage dar, um die Bewegungen dieser Körper als Kreisbewegungen aufzufassen. Das erklärte die in etwa periodische Wiederholung der Bewegung der Gestirne. Denn war die Kreisbahn einmal beendet, begann der Zyklus von neuem. Die Sterne wurden dabei als bewegungslose Fixsterne betrachtet. Ohne präzise Messungen und Beobachtungen war dieses Modell konsistent mit den Naturbeobachtungen. Da es in Einklang mit den kirchlichen Lehren stand, überdauerte dieses Aristotelische Weltbild viele Jahrhunderte.
Aristoteles versuchte auch die Bewegung fallender Körper auf der Erde zu erklären. Der gerade Fallweg war für ihn ein Beleg dafür, dass die Erde ruhe. Diese ersten Überlegungen mit dem Prinzip 'Naturbeobachtung – erklärendes Modell' stehen bereits im Geiste der fast 2000 Jahre späteren Aufklärungsepoche (Experiment – Theorie). Aristoteles legt hier somit die ersten (wenn auch nicht ganz überzeugenden) phänomenologischen Modelle für die Schwerkraft vor.

Das Epizykel-Modell nach Ptolemäus

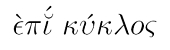Eine kleine Modifikation erfuhr das Modell für die Bewegungen von Sonne, Mond und Planeten durch den alexandrinischen Gelehrten Claudius Ptolemäus (100 – ca. 160 n. Chr.). Er ist der Autor des ersten Standardwerks der Astronomie, das unter dem Namen Almagest bekannt wurde. Auch das Ptolemäische Weltbild ist geozentrisch und fußt auf 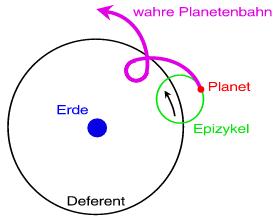Kreisbahnen – allerdings wurde Komplexität dadurch ins Spiel gebracht, dass sich die Mittelpunkte von Kreisbahnen ihrerseits auf Kreisen, den so genannten Deferenten, bewegen. Der Kreis auf dem Deferenten heißt Epizykel (grch. 'Überkreis'). Eine Illustration dieses einfachen, geometrischen Modells zeigt die Abbildung links. Das Modell wahrte einerseits die Sonderrolle der Kreisfigur, die von den Aristotelikern als vollkommen angesehen wurde; andererseits vermag das Epizykel-Modell kompliziertere Bewegungen zu erklären: So war damals schon die rückläufige Bewegung (z.B. bei Mars) bekannt, die im Aristotelischen Weltbild vollkommen unverständlich war. Wie die Illustration zeigt, weist die resultierende Bahnform des Planeten Schleifen auf, in denen sich der Planet von der Erde aus gesehen rückläufig bewegt. Die Ptolemäische Epizykel-Theorie erklärte demnach die beobachtete Rückläufigkeit. Aber leider waren nicht alle Bewegungen der Himmelskörper mit Epizykeln widerspruchsfrei zu beschreiben.

Galilei – Gravitationsforscher und Pionier der Astronomie

Der italienische Physiker, Mathematiker und Philosoph Galileo Galilei (1564 – 1642) ist der erste, der systematisch und mathematisch die Gravitation erforschte. Galilei soll Fallexperimente am Schiefen Turm von Pisa durchgeführt haben, um seine Hypothese zu testen, ob Gewicht oder Dichte eines Körpers darüber entscheiden, wie schnell der Körper fällt. Galilei führte auch zahlreiche mechanische Experimente mit Pendeln und mit rollenden Objekten auf der schiefen Ebene durch. Er erklärte die Bahn von Geschossen im Schwerefeld durch eine Überlagerung zweier Bewegungen, nämlich gleichmäßig beschleunigter Fallbewegung und gleichförmig geradliniger Geschossbewegung (Superpositionsprinzip) und bewies die Parabelbahn.
Randbemerkungen: Bedeutsam und bekannt ist Galileo Galilei für seine astronomischen Entdeckungen: er verbesserte das Holländische Fernrohr, das Hans Lipperhey erfunden hatte und beobachtete 1610 erstmals die Krater des Mondes, die Zusammensetzung der Milchstraße aus Sternen und vier Monde des riesigen Gasplaneten Jupiter (Galileiischen Monde). Seine Entdeckung der Venusphasen bestätigte das Kopernikanische, heliozentrische Weltbild in der Beobachtung. Die Entrückung der Erde aus dem Zentrum der Welt und die Annahme ihrer Bewegung führte zur offenen Auseinandersetzung mit der katholischen Kirche. 1633 wurde Galilei des schweren Verdachts auf Ketzerei nach Rom vorgeladen, und im gleichen Jahr schwor er von der heliozentrischen Lehre ab. 1992 wurde Galilei von der katholischen Kirche durch Papst Johannes Paul II. offiziell rehabilitiert.
Albert Einstein, zu dem wir im Verlauf dieses Lexikoneintrags noch kommen werden, schrieb über Galilei:

Alles Wissen über die Wirklichkeit geht von der Erfahrung aus und mündet in ihr. Rein logisch gewonnene Sätze sind mit Rücksicht auf das Reale völlig leer. Durch diese Erkenntnis und insbesondere dadurch, dass er sie der wissenschaftlichen Welt einhämmerte, ist Galilei der Vater der modernen Physik, ja, der modernen Naturwissenschaft überhaupt geworden.

(entnommen aus Die Klassiker der Physik, S. 334, Verlag Hoffmann und Campe, 2004)

Newtonsche Gravitation

Die Erforschung der Gravitation hat durch den englische Universalgelehrten Sir Isaac Newton (1643 – 1727) einen gewaltigen Durchbruch erlangt. Newton ist für viele Leistungen berühmt geworden: die Begründung der Differential- und Integralrechnung, Entdeckungen in der Optik (Farbtheorie, Korpuskulartheorie des Lichts) und die heute nach ihm benannte Gravitationstheorie. Die Newtonsche Gravitationsphysik ist die erste Gravitationstheorie, die den Namen Theorie verdient, weil sie ein konsistentes, umfassendes Konzept und nicht bloß Phänomenologie oder Hypothese ist. Newton stellte diese Theorie in seinem Werk Philosophiae naturalis principia mathematica dar. Dieses Werk Principia ist das erste Standardwerk der theoretischen Physik überhaupt! Der Titel ist eine Replik auf die Principia Philosophiae von René Descartes.
Newton widmete sich 1665 der Optik und Gravitation. Die Geschichte mit dem vom Baum fallenden Apfel, der Newton am Kopf getroffen und ihn zur Gravitationstheorie inspiriert haben soll, ist wohl ein Mythos – Newton schrieb lediglich, dass ein fallender Apfel ihn veranlasste, über Gravitation nachzudenken. 27jährig wurde Newton (auf Empfehlung des Vorgängers dieses Amts) Lukasischer Professor der Mathematik – ein Lehrstuhl der Universität Cambridge, den heute übrigens Stephen Hawking inne hat. Newton kannte die astronomischen Beobachtungen von Johannes Kepler und dessen Entdeckung, dass die Planeten sich auf Ellipsenbahnen um die Sonne bewegen. 1666 begann Newton nach einer physikalischen Erklärung dieser rein empirischen Kepler-Gesetze zu suchen. Das zweite Keplersche Gesetz (Flächensatz) konnte er 1679 dadurch erklären, dass es eine anziehende Zentralkraft geben müsse, die von der Sonne ausgehe.
Ein Treffen dreier Mitglieder der Royal Society im Jahre 1684 sollte zum Schlüsselereignis werden: Hier trafen sich Newtons Widersacher Robert Hooke, der Astronom Edmond Halley und der Architekt Christopher Wren. Sie diskutierten über eine Kraft, die proportional zum umgekehrten Abstandsquadrat sei und die Planetenbewegung bestimme. Angeregt durch diese Diskussion fragte Halley bei Newton nach der Bahnform eines Himmelskörpers, die aus diesem Kraftgesetz resultiere. Newton hatte diese Fragestellung bereits Jahre zuvor berechnet und wusste, dass es eine Ellipsenbahn sein müsse. Die detaillierte Ausarbeitung dieser Rechnung mündete schließlich in eine anderthalbjährige Schaffensphase Newtons und in die Publikation der Principia 1687.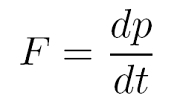
Das Buch I der Principia enthält die drei Bewegungsgesetze, die heutzutage als Newtonsche Gesetze gelehrt werden, nämlich das Trägheitsgesetz, das dynamische Grundgesetz und das Reaktionsprinzip (actio = reactio). Das in der Gleichung links dargestellte dynamische Grundgesetz ist in der Schulphysik viel bekannter in der Form F = m a, aber dieser Fall gilt nur, falls die Masse zeitunabhängig, m ≠ m(t), ist. Das ist im Allgemeinen aber nicht der Fall (z.B. bei der so genannten Raketengleichung: eine fliegende Rakete verliert Treibstoff und daher Masse), so dass das Gesetz als zeitliche Ableitung des Impulses p formuliert werden muss. Das Buch II ist ein Lehrbuch über Strömungsmechanik. Schließlich stellt Newton in Buch III sein Gravitationsgesetz vor und demonstriert die Gültigkeit dieser Gravitationstheorie anhand der Bewegungen von Planeten und Kometen.
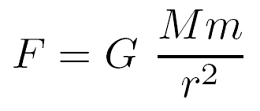Die Newtonsche Theorie besagt auch, dass sich Gravitation instantan ausbreite, d.h. ohne Laufzeitverzögerung. Außerdem haben Zeit und Raum einen absoluten Charakter in der Newtonschen Physik. Im nächsten Abschnitt werden wir sehen, dass sich diese Eigenschaften der Gravitation als nicht haltbar erweisen und die Newtonsche Gravitation zur Einsteinschen Gravitation verallgemeinert werden muss.

Einsteins Allgemeine Relativitätstheorie

Im Jahr 1916 präsentierte Albert Einstein (1879 – 1955) eine vollkommen neuartige Sicht auf die Gravitation. In diesem Jahr publizierte er die Allgemeine Relativitätstheorie (ART), eine (unquantisierte) Gravitationstheorie, die die Gravitation nicht als Kraft, sondern als geometrische Eigenschaft von Raum und Zeit auffasst. Dieser Gravitationstheorie vorangegangen war die Spezielle Relativitätstheorie (SRT), die keine Gravitationstheorie darstellt, die jedoch die revolutionäre Neudefinition der Begriffe Energie, Masse, Zeit und Raum einleitete. 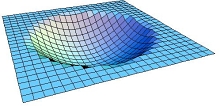Gemäß Einstein sind Raum und Zeit miteinander verknüpft zu einem vierdimensionalen Gebilde: der Raumzeit. Während die Raumzeit in der SRT noch flach ist, wird sie in der ART gekrümmt. Wie man sich vereinfacht in einer zweidimensionalen Variante eine gekrümmte Raumzeit vorstellen kann, zeigt die Abbildung links. Die 'Beule' in dieser 2D-Raumzeit kommt durch Massen zustande. Einstein hat bereits in der SRT erkannt, dass Energie und Masse äquivalent sind, was in der berühmten Formel E = mc² zusammengefasst wird. Die Konsequenz: Massen und alle Formen von Energie verursachen 'Beulen' in der Raumzeit. Eine (kräftefreie) Bewegung durch die Raumzeit ist nun nicht in beliebiger Form möglich, sondern nur entlang bestimmter Kurven, die in der ART Geodäten genannt werden. Die Geodäten 'schlängeln' sich durch die 'verbeulte Raumzeit' – wie das genau geschieht, diktieren Rechengesetze der Differentialgeometrie. Die Bewegung entlang der Geodäten nehmen wir als Gravitation war. Wir bewegen uns also täglich unter dem Einfluss der gekrümmten Raumzeit!
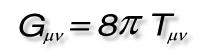Die Abstraktionsleistung ist gewaltig, um dieses neue Bild der Gravitation halbwegs fassen zu können. Niemand kann sich eine vierdimensionale, gekrümmte Raumzeit vorstellen, aber unterdrückt man einige Dimensionen, so lassen sich zumindest Raum-Zeit-Diagramme zeichnen, die beim Verständnis helfen. Einsteins neue Gravitationstheorie lässt sich in eine einzige, aber leider komplizierte Formel fassen: die Feldgleichungen der ART. Diese übersichtliche Gleichung steht rechts (hier zur Vereinfachung ohne kosmologische Konstante Λ). In dieser knappen Form besagt die Formel direkt, das die gekrümmte Raumzeit, die in G steckt, von Masse und Energie, die in T stecken, hervorgerufen wird; die Gleichung enthält weiterhin den Aspekt, dass die Beulen der Raumzeit die Bewegung diktieren. Allerdings täuscht die Einfachheit dieser Formel! Hinter den Symbolen G und T verbergen sich mathematische Objekte, die Tensoren genannt werden. Genauer gesagt ist G der Einstein-Tensor und T heißt Energie-Impuls-Tensor. Im Allgemeinen sind diese Objekte sehr kompliziert, bestehen aus mehreren Komponenten und variieren von Raumzeitpunkt zu Raumzeitpunkt.
Ein Gravitationsfeld der Newtonschen Physik wird nun also durch eine Raumzeit in der Einsteinschen Physik ersetzt. Die Raumzeit ist Lösung von Einsteins Feldgleichung und eindeutig beschrieben durch die Metrik (den metrischen Tensor g) oder alternativ durch das Linienelement. Die Gravitationskraft Newtons wird abgelöst von den Christoffel-Symbolen, dem Riemann-Tensor und anderen mathematischen Größen der ART (1-Formen, 2-Formen, Killing-Felder, Kretschmann-Skalar, Ricci-Tensor, Ricci-Skalar etc.). Häufig ist von Interesse wie sich Testobjekte durch eine gekrümmte Raumzeit bewegen. Um dieses Problem zu lösen muss die Geodätengleichung gelöst werden. Für Licht heißt dieses Verfahren relativistisches Ray Tracing.
Raumzeiten sind im Allgemeinen auch dynamisch, d.h. sie verändern ständig ihre Krümmungseigenschaften. Das geschieht insbesondere bei Gravitationswellen, die sich ebenfalls mit Einsteins Theorie beschreiben lassen. Es handelt sich um Beulen in der Raumzeit, die sich mit der Vakuumlichtgeschwindigkeit c ausbreiten. Das ist ein wichtiger Unterschied zur Newtonschen Physik: Gravitation breitet sich in Einsteins Theorie nicht beliebig schnell, sondern exakt mit c aus.
Einsteins ART hat sich vielfach in Experimenten bewährt. Eine Reihe experimenteller Tests und Erfolge sowie die Theorie selbst werden im Lexikoneintrag Allgemeine Relativitätstheorie in vielen Einzelheiten vorgestellt.

relativistische Astrophysik

Einsteins Theorie hat auch die Astronomie stark geprägt: Viele astrophysikalische Vorgänge können nur mit der Einsteinschen Gravitation zufrieden stellend behandelt werden. Der Gravitationskollaps zu einem kompakten Objekt (z.B. Neutronensterne) ist ein Beispiel dafür. In der Akkretionsphysik wurden Modelle etabliert, die auf der ART basieren. Aber auch auf der ganz großen Raumskala, ist die Einsteinsche Theorie die richtige Wahl: die Kosmologie ist relativistisch. So kann auch das komplette Universum als Lösung der Einsteinschen Feldgleichung aufgefasst und mit der Robertson-Walker-Metrik beschrieben werden. Die Friedmann-Weltmodelle, die aus der ART hervorgehen, beschreiben exzellent viele Beobachtungen der experimentellen Kosmologie (siehe dazu kosmische Hintergrundstrahlung, Supernovae Typ Ia). Eine Reihe beobachteter Phänomene sind im Rahmen der Newtonschen Gravitation nicht zu verstehen, z.B. gravitative und kosmologische Zeitdilatation, Rotverschiebung und Gravitationsrotverschiebung sowie Frame-Dragging.

kosmologische Bedeutung der Gravitation

Die Bedeutung der Gravitation für das ganze Universum begründet sich in zwei Eigenschaften, die eingangs schon erwähnt wurden: Gravitation hat im Prinzip eine beliebige Reichweite, und sie ist nicht abzuschirmen. Aufgrund der ersten Eigenschaft kann Gravitation auch über extrem große Distanzen wirken – bis Milliarden von Lichtjahren, also Skalen, die so groß sind, wie der Kosmos selbst. Aufgrund der zweiten Eigenschaft, Nichtabschirmbarkeit, gibt es kaum eine Möglichkeit Gravitation aufzuhalten (es sei denn durch Antigravitation – dazu mehr im nächsten Abschnitt). Die Konsequenz ist das, was Astrophysiker die gravitative Instabilität nennen. Anschaulich kann man das so beschreiben, dass die Materie durch den Einfluss der Gravitation anfängt zu 'klumpen': Wird die Jeans-Masse lokal für eine Massenansammlung überschritten, so setzt der Gravitationskollaps ein. Später fragmentiert dieser Klumpen zu kleineren. Diese Szenarien sind wesentlich, um die Herkunft der großräumigen Struktur im Kosmos zu begreifen. Aus der anfänglichen Verteilung des 'Urgases', das in der primordialen Nukleosynthese entstand, bildete sich die erste Sterngeneration (Population III) durch gravitative Instabilitäten. Durch den Einfluss der Gravitation entstanden daraus die ersten Galaxien – so lief es zumindest in einem hierarchischen Wachstumsszenario ab.

Antigravitation

Die relativistische Kosmologie hat eine Form der Gravitation hervorgebracht, die feuchte Augen bei Science-Fiction-Fans hervorruft: Antigravitation. Um den Zusammenhang zu erklären, müssen wir einen Blick auf die moderne Kosmologie werfen. Die Dynamik der bereits angesprochenen Friedmann-Weltmodelle wird von den Energieformen im Kosmos bestimmt. Die 'normale', baryonische Materie, aus der wir auch selbst bestehen, ist dabei eine Energieform, dessen Bedeutung jedoch so gut wie irrelevant ist. Eine andere Materieform, die Dunkle Materie, ist viel häufiger im Universum anzutreffen. Sie beeinflusst nicht nur die Dynamik und Entwicklung von Galaxien, sondern auch vom Kosmos insgesamt. Ihr relativer Anteil beträgt etwa ein Drittel. Was sich allerdings konkret hinter der Dunklen Materie verbirgt ist ein Rätsel – die aktuellen Vorstellungen werden im Eintrag Dunkle Materie präsentiert.
Kommen wir nun zum entscheidenden Teil: die verbleibenden zwei Drittel der Energie im Universum gehen auf das Konto der Dunklen Energie. Was genau hinter dieser mysteriösen, kosmischen Zutat steckt, ist ein brisantes und hochaktuelles Forschungsgebiet. Es ist keine konkrete Materieform, sondern die Physiker favorisieren, dass sich das überall im Universum fein verteilte Quantenvakuum selbst als kosmologisch relevante Energieform manifestiert. Das astronomische Beobachtungsfaktum ist eine beschleunigte Expansion des Kosmos. Im Standardmodell der Kosmologie wird das durch die Existenz der Dunklen Energie erklärt (Alternativen werden im Eintrag Dunkle Energie aufgezeigt).
Das Besondere an der Dunklen Energie ist ihre Zustandsgleichung, weil sie einen negativen Druck aufweist. Das klingt recht unphysikalisch, aber vermag die Beobachtungen erstaunlich gut zu erklären. Der so genannte w-Parameter liegt laut astronomischen Beobachtungen nahe bei w = -1. Damit wird aus einer ganzen Palette von Modellen für Dunkle Energie ein bestimmtes von der Natur offensichtlich bevorzugt, und zwar die kosmologische Konstante, die niemand Geringeres als Einstein 1917 eingeführt hat. Sie hat gerade den passenden w-Parameter – und sie variiert zeitlich nicht, was ebenfalls zu aktuellen Beobachtungen an weit entfernten, explodierenden Weißen Zwergen passt. Eine solche Zustandsgleichung sorgt für eine Expansion des Universums, die als Antigravitation aufgefasst werden darf. Denn Dunkle Energie wirkt der Gravitation entgegen. Anhand der Friedmann-Gleichung kann man zeigen, dass zu späteren Entwicklungsepochen hin, der Einfluss der antigravitativen Dunklen Energie gewinnt. Die aktuelle Datenlage sagt eine ewige und immer schnellere Expansion des Universums voraus. Am Ende steht ein kalter Kosmos, in dem vermutlich nur noch Schwarze Löcher (mit unterschiedlichen Massen und Drehimpulsen) und vielleicht noch Schwarze Zwerge existieren.

Schwerkraft auf Quantenniveau

Allerdings hat auch die Einsteinsche Gravitation ihre Grenzen. Dem aufmerksamen Leser wird nicht entgangen sein, das die ART mit dem Attribut unquantisiert versehen wurde. Das bedeutet, dass die Konzepte der zweiten großen, physikalischen Theorie des 20. Jahrhunderts, der Quantentheorie, keine Beachtung in Einsteins Theorie gefunden haben. Das geschah nicht aus Ignoranz: Gerne hätte Einsteins eine solch umfassende Feldtheorie erfunden; tatsächlich arbeitete er in seinen letzten Lebensjahren an dieser übergeordneten Theorie – doch diese Herausforderung war selbst für Einstein zu groß.
Eine solche quantisierte Gravitationstheorie wird mit dem Etikett Quantengravitation versehen. Die Motivation dafür ist, das Quanteneffekte auch bei gravitativen Vorgängen wichtig werden, nämlich dann, wenn starke Gravitation und kleine Längenskala zusammenkommen. Wo passiert denn so etwas in der Natur? Es geschieht bei Objekten, die von der Gravitation dominiert werden und die sehr kompakt sind, nämlich bei Schwarzen Löchern. Laut Einsteins ART lauert in jedem Schwarzen Loch ein punktförmiges Objekt, in dem die Krümmung der Raumzeit ins Unermessliche wächst. Diese phantastischen Orte heißen Krümmungssingularitäten (und sind streng von den Koordinatensingularität zu unterscheiden!). Aber gibt es tatsächlich Punkte in der Natur? Die Konzepte der Quantentheorie negieren das. Die Physik Schwarzer Löcher ist eine erste Motivation, um sich an eine Ausarbeitung einer Quantengravitation zu wagen.
Eine zweite Motivation liefert die Kosmologie des frühen Universums: die Hochenergiephysiker haben herausgefunden, dass unsere Welt der vier Naturkräfte nicht im jungen Kosmos anzutreffen war. Das Temperaturmilieu führte dazu, dass einige Kräfte miteinander 'verschmolzen': Je heißer es ist, umso weniger fundamentale Naturkräfte sind vorhanden. Der 'Gipfel' dieser Unifikation soll als Urkraft in der Planck-Ära vorgeherrscht haben. Die Gravitation sei die erste gewesen, die sich mit Expansion und dadurch bedingter Abkühlung, von der Urkraft abgespalten haben soll. Die Fachleute nennen diesen Übergang Symmetriebrechung. Nach der ersten Symmetriebrechung lagen zwei fundamentale Naturkräfte vor: Gravitation und X-Kraft in der so genannten GUT-Ära. Die Frage, die die Hochenergie- und Teilchenphysiker antreibt, ist, wie man die Gravitation mit den anderen Quantenkräften einheitlich als Quantenfeldtheorie beschreiben könnte.
Im Quantenbild ist die Gravitation weder Kraft, noch gekrümmte Raumzeit: sie ist Eichboson. So nennen die Quantenfeldtheoretiker quantisierte 'Botenteilchen', die die Kraft vermitteln. Im Falle der Gravitation hat dieses Austauschteilchen auch einen Namen, nämlich Graviton. Die Eigenschaften der Gravitation verlangen einige Eigenschaften des Gravitons, z.B. dass es Spin 2 haben muss. Helle Aufregung ist daher entstanden, als in den 1970er Jahren eine Theorie entdeckt wurde, die Spin-2-Teilchen enthält. Diese Theorie war eine der ersten Varianten der Stringtheorien. Damit wurden die Stringtheorien schlagartig zum interessantesten Kandidaten einer Quantengravitation. Auch im 21. Jahrhundert gehören die Stringtheorien zu den aktivsten Gebieten der theoretischen Physik. Wie unter dem Eintrag Stringtheorien erläutert wird, steckt diese Forschung in einem Wechselbad aus Erfolgen und Zweifel. Eine Problematik besteht beispielsweise darin, dass bis heute dieses Botenteilchen der Gravitation nicht experimentell entdeckt wurden. Auf der Erfolgsseite kann die Stringtheorie eine moderne Sichtweise auf Gravitation und Eichung verbuchen: So wurde die AdS/CFT-Korrespondenz entdeckt, die auf einen tief liegenden Zusammenhang zwischen Gravitation und Teilchentheorien hinweist. Inzwischen wurde das Prinzip verallgemeinert und wird zurzeit erforscht (gauge/gravity duality). Weitere Erfolge sind Modelle die sich unter der Bezeichnungen Branenwelt versammeln. Diese Modelle, beispielsweise die Randall-Sundrum-Modelle oder das Zyklische Universum, haben ganz erstaunliche Eigenschaften und vermögen bislang Unverstandenes (Koinzidenzproblem, Schwäche der Gravitation, Kleinheit der kosmologischen Konstante, Ursache des Urknalls etc.) auf sehr elegante Weise zu erklären.
In den 1980er Jahren ist eine andere Variante der Quantengravitation hinzugekommen, die einen etwas anderen Ansatz verfolgt. Nah an den Konzepten der Einsteinschen Gravitation (siehe z.B. unter dem Zungenbrecher Diffeomorphismusinvarianz), betont die Loop-Quantengravitation (LQG) den geometrischen Charakter der Gravitation. Im Rahmen dieser Theorie ist die Quantisierung der Raumzeit in so genannte Wilson-Loops tatsächlich gelungen. Mit den Konzepten der LQG können in der Tat die Singularitäten der ART beseitigt werden! Das gilt sowohl für die Krümmungssingularität Schwarzer Löcher, als auch für die Urknallsingularität. Die Theorie und ihre Prognosen werden unter dem Eintrag Loop-Quantengravitation vorgestellt.
Stringtheorien und Loop-Quantengravitation sind die beiden bedeutenden Anwärter, die das Potenzial haben, die Einsteinsche Gravitation zu erweitern. Der Skeptiker mag einwenden, dass es bislang keine überzeugenden Hinweise aus Experimenten gibt, die diesen Quantengravitationen den Status einer bewährten Gravitationstheorie verleihen würden. Das ist der gravierende Unterschied zu den Theorien von Newton und Einstein. Die Gravitationsforscher bleiben jedoch sehr aktiv, um diesen Nachweis zu erbringen. Wichtige, neue Impulse werden von der Teilchenbeschleunigeranlage der modernsten Generation erwartet: dem Large Hadron Collider (LHC).

Approximatives, Spekulatives & Exotisches

Mit dem bisher Gesagten könnte der Eintrag über Gravitation eigentlich schließen, aber es sollte auch etwas über Gravitationstheorien abseits des Mainstreams gesagt werden. Im Folgenden sollen approximative und alternative Gravitationstheorien knapp vorgestellt werden.

Gravitationstheorien mit Torsion

Bei den Gravitationstheorien mit Torsion verschwindet der Torsions-Tensor nicht. Die ART hingegen ist torsionsfrei, was symmetrische Christoffel-Symbole zur Folge hat. Bei Gravitationstheorien mit Torsion handelt man sich also zusätzliche Terme ein, die es in der ART gar nicht gibt. Das gestaltet diese Alternativen komplizierter als die ART.

Fernparallele Gravitation

Fernparallele Gravitation oder kurz Fernparallelismus wurde 1928 von Einstein als neue Gravitationstheorie mit Torsion erfunden. In dieser Theorie ist Schwerkraft nicht eine Folge der Krümmung einer Raumzeit, sondern vielmehr eine Folge der Verdrillung der Raumzeit (Torsion). Die Gravitationsforscher konnten zeigen, dass Fernparallelismus und ART als gleichwertige Formulierungen der Gravitation aufgefasst werden können. Aktuell publizieren Gravitationstheoretiker die entsprechenden fernparallelen Pendants zu den gewohnten Lösungen der Feldgleichungen der ART.
In der modernen Gravitationsphysik wird außerdem versucht, noch andere Formen des Fernparallelismus zu konstruieren, die nicht als Analog der ART aufgefasst werden können. In diesen fernparallelen Gravitationstheorien (engl. teleparallel gravity) können völlig neue Einsichten in die Natur der Schwerkraft gewonnen werden. Die Hoffnung ist, auf diesem Wege eine Gravitationstheorie zu finden, die der Einsteinschen Theorie übergeordnet ist oder interessante Querverbindungen zu Eich-, Feld- und Quantengravitationstheorien ziehen zu können.

Skalar-Tensor-Theorien

Bei den Skalar-Tensor-Theorien liegt die Idee zugrunde, dass neben dem metrischen Tensor ein weiteresSkalarfeld vorhanden ist. Dieses Feld koppelt an den Krümmungsskalar (Ricci-Skalar), aber nicht an den metrischen Tensor. Die ART kann aus einem Wirkungsfunktional abgeleitet werden, das in der Literatur Einstein-Hilbert-Wirkung genannt wird. Hier fehlt ein Skalarfeld. Das Wirkungsfunktional der Skalar-Tensor-Theorien enthält entsprechend zusätzliche Terme. Das Skalarfeld kann nun mit unterschiedlichen Eigenschaften ausgestattet werden: es kann in jedem Raumzeitpunkt konstant sein, oder es kann variieren. Im Falle einer Variation kann davon gesprochen werden, dass die Newtonsche Gravitationskonstante G nun keine fundamentale Naturkonstante mehr ist. Es gibt viele Varianten der Skalar-Tensor-Theorien. Die bekannteste ist die Brans-Dicke-Theorie.

MOND-Theorie

Die MOND-Theorie (siehe dort für Details), die 1983 von dem israelischen Physiker Mordehai Milgrom erfunden wurde, ist eine Gravitationstheorie, die das Newtonsche Gravitationsgesetz um einen zusätzlichen Faktor korrigiert. Dieser Faktor hängt von der Beschleunigung ab und vermag u.a. das Rotationsverhalten vieler Spiralgalaxien sehr gut zu erklären – erstaunlicherweise ohne Dunkle Materie.

TeVeS

TeVeS stellt gewissermaßen einen 'Ableger' von MOND dar, weil sie aus der relativistischen Erweiterung von MOND entdeckt wurde. Jacob D. Bekenstein hat 2004 diese Tensor-Vektor-Skalar-Gravitationstheorie formuliert, die sozusagen noch einen Schritt weiter geht als die Skalar-Tensor-Theorien, weil ein zusätzliches Vektorfeld enthalten ist. Aktuelle Untersuchungen zeigen, dass TeVeS viele Beobachtungen der modernen Kosmologie gleichermaßen zu erklären vermag wie die Einsteinsche Theorie. Dennoch ist diese recht neue Theorie umstritten und befindet sich erst am Anfang eines langwierigen Evaluierungs- und Testprozesses.

Post-Newtonsche Approximation

Die so genannte Post-Newtonsche Approximation der Einsteinschen Gravitation wird gewonnen, wenn man den Grenzübergang v/c « 1 von der ART zur Newtonschen Physik durchführt, aber Terme der linearen Ordnung v/c belässt. Pseudo-Newtonsche (PN) Gravitation ist so etwas wie eine 'Zwittergravitation zwischen Einstein und Newton'. Sie bietet sich insbesondere in der Himmelsmechanik an, wenn hinreichend gute Resultate für Bahnbewegungen gewünscht sind, aber nicht voll relativistisch gerechnet werden kann oder soll. Die Ermittlung der approximativen Gravitationsgleichungen sind zwar recht aufwendig, können aber sehr bequem in Computercodes zur Lösung des Schwerkraftproblems implementiert werden. So werden PN-Codes gerne zur Berechnung von Phänomenen mit Gravitationswellen herangezogen. Zur Erhöhung der Genauigkeit und damit zur noch besseren Annäherung an die Einsteinsche Gravitation, kann die entsprechende Ordnung v/c einfach erhöht werden, z.B. PN 5. Ordnung.
Eine analoge Methodik wird von Gravitationsforschern zur Approximation anderer Gravitationstheorien, z.B. einer Skalar-Tensor-Theorie, durchgeführt. Das unterstreicht die Universalität und Brauchbarkeit des Näherungsverfahrens.

Pseudo-Newtonsche Gravitation

Im Rahmen der Pseudo-Newtonschen Gravitation wird eine Annäherung an die Einsteinsche Gravitationsphysik angestrebt. Punktmassen werden relativistisch mit der Schwarzschild-Lösung beschrieben. Der pseudo-Newtonsche Ansatz besteht in einem 1980 von B. Paczynski und P. Wiita vorgeschlagenen Modell, das das Schwerefeld einer Punktmasse nachahmt. Dazu wird nicht die typische und mathematisch aufwendige Tensorschreibweise benutzt, sondern die Potentialformulierung, die anmutet wie eine Newtonsche Gravitationsphysik. Der wesentliche Unterschied besteht darin, dass nicht das übliche Newtonsche Potential verwendet wird, sondern das so genannte Paczynski-Wiita-Potential. Dieses neue Potential skaliert mit dem Schwarzschild-Radius und vermag entsprechend bis zu einem gewissen Grad die Gravitationseffekte um eine Punktmasse und insbesondere die Effekte nahe einem statischen Schwarzen Loch zu simulieren. Die Genauigkeit mit der die relativistischen Effekte imitiert werden können, beträgt etwa 10-20%, sofern Radien außerhalb der marginal stabilen Bahn (hier bei sechs Gravitationsradien) betrachtet werden.

Gravitation mit Extradimensionen

Eine interessante Variante einer Gravitationstheorie, sind die Feldtheorien mit Extradimensionen. Es handelt sich um die Theorien, die weitere Raumdimensionen, nicht jedoch weitere Zeitdimensionen zulassen. Das besondere ist, dass die Gravitation auch in den höheren Raumdimensionen wirkt – nicht jedoch die anderen Naturkräfte. Damit erklären Gravitationstheorien mit zusätzlichen Raumdimensionen, die in der modernen Sprache auch Branenmodelle genannt werden, sehr elegant das Hierarchieproblem in der Physik.
Der historisch erste Vorschlag war die Kaluza-Klein-Theorie, die als 5D-Feldtheorie auf eine Vereinheitlichung des Elektromagnetismus und der ART abzielte. Die Theorie scheiterte damals, enthält aber Aspekte, die auch heute wieder (im Rahmen der Stringtheorien) interessant sind, z.B. die Kompaktifizierung der Extradimensionen. Interessanterweise können einige Theorien mit Extradimensionen auf die Form von Skalar-Tensor-Theorien gebracht werden. Mit anderen Worten: die Eigenschaften der Extradimensionen können als Skalarfeld identifiziert werden. Beispiele dafür sind das Radion bzw. Dilaton.
Im Wissensportal werden folgende Branenmodelle im Detail vorgestellt: das ADD-Szenario, die Randall-Sundrum-Modelle, das DGP-Szenario und das Zyklische Universum. Alle Modelle geben wertvolle, neue Einsichten in physikalisches Neuland. Allerdings ist bislang nicht klar, ob in der Natur tatsächlich diese Form der Physik realisiert ist. Eventuell bringt die Klärung der Pioneer-Anomalie diesbezüglich neue Erkenntnisse.

f(R)-Gravitation

Die f(R)-Gravitation (siehe diesen Eintrag für Einzelheiten) ist eine Modifikation von Einsteins ART. Im Wirkungsfunktional werden dabei nichtlineare Zusatzterme berücksichtigt, die eine beliebige Abhängigkeit von dem Krümmungs- oder Ricci-SkalarR haben können – daher die Bezeichnung f(R). Die Dynamik der Gravitation wird bestimmt von einer Feldgleichung, die aus diesem neuen Wirkungsfunktional resultiert. Die Nichtlinearitäten sorgen dabei für neue Effekte, dass beispielsweise die Gravitation auch bei schwachen Krümmungen wesentlich oder sogar zu einer beschleunigten Ausdehnung der Raumzeit führen kann. Der letztgenannte Aspekt macht die f(R)-Modell interessant für die Kosmologie, weil ein f(R)-Szenario die Rolle der Dunklen Energie übernehmen könnte. Derzeit werden viele f(R)-Familien vorgestellt, analysiert, falsifiziert und ihre Bedeutung für die Gravitationsforschung, Astrophysik und Kosmologie ausgelotet. Damit diese Alternative sich etablieren kann, sind noch viele erfolgreich absolvierte Bewährungsproben notwendig.

Bedeutung der Gravitation für den Menschen

Will man die Milliarden dauernde Entwicklung des Universums auf den Punkt bringen, so stellt man Folgendes fest: Wir erfahren Gravitation nicht nur täglich als Kraft, die uns am Erdboden hält, sondern ihre sehr subtilen und einzigartigen Eigenschaften, die sie unter allen Naturkräften auszeichnen, sind überhaupt dafür verantwortlich, dass wir hier sind! Die Auswirkungen der Gravitation auf unser Leben manifestieren sich in vielen Aspekten: Die Leben spendende Energie der Sonne wäre ohne Gravitation gar nicht vorhanden; der Lauf der Gestirne, der unsere kulturell verfestigten Zyklen wie Tag, Monat und Jahr formte, ist ebenfalls ein Produkt der Gravitation; ohne Gravitation hätte die Erde keine Atmosphäre, deren Gase die Evolution des Lebens mit einer phantastischen Vielfalt bereichert haben – diese Liste ließe sich weiter fortsetzen. Wir sollten daraus den Schluss ziehen, etwas bodenständiger zu werden und nicht abzuheben, sondern dem gewichtigen Einfluss der Gravitation in Demut, aber nicht mit Schwermut, zu begegnen.

Literaturtipps

• C. W. Misner, K. S. Thorne & J. A. Wheeler: Gravitation, Freeman San Francisco, 1973
• Die Klassiker der Physik – E = mc², Verlag Hoffmann und Campe, 2004