Die Friedmann-Weltmodelle beschreiben die Dynamik des Universums als Ganzes. Mit ihrer Hilfe lassen sich Szenarien für dynamisch ganz unterschiedliche Universen entwerfen.

dynamische und statische Modell-Universen

Damit sind Friedmann-Universen wesentlicher Gegenstand der Kosmodynamik. Auch Albert Einsteins Statisches Universum ist als Grenzfall enthalten. Geeignete kosmologische Parameter ermöglichen eine Klassifikation in nicht-statische, also dynamische, und statische Lösungen. Die Behandlung und Untersuchung der Lösungsmannigfaltigkeiten der Friedmann-Weltmodelle nennen Kosmologen manchmal auch Friedmannologie. Formal folgen die Friedmann-Weltmodelle oder FLRW-Modelle (Friedmann-Lemaître-Robertson-Walker-Modelle) aus folgenden vier Zutaten:

• kosmologisches Prinzip,
• Weylsches Postulat,
• Robertson-Walker-Metrik und
• Feldgleichung der Allgemeinen Relativitätstheorie mit kosmologischer Konstante (mit Lambda-Term).

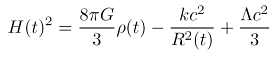Friedmann-Weltmodelle sind also eingebettet in eine relativistische Kosmologie. Das Linienelement der Robertson-Walker-Metrik wird in die Einsteinschen Feldgleichungen mit Lambda-Term eingesetzt und führt auf ein System zweier unabhängiger Differentialgleichungen zweiter Ordnung, den Friedmann-Gleichungen. Sie sind von fundamentaler Bedeutung für die moderne Kosmologie. Die beiden Gleichungen können zu einer einzigen Differentialgleichung erster Ordnung (siehe rechts) kombiniert werden. Diese Gleichung ist erster Ordnung, weil der Hubble-Parameter H(t) die erste Ableitung von R(t) enthält. Die Gleichung wird für unterschiedliche kosmologische Parameter betrachtet und führt so auf unterschiedliche Modelluniversen.

Historische Wegbereiter der modernen Kosmologie

Die Friedmann-Gleichungen fand der russische Mathematiker und Astronom Alexandr A. Friedmann 1922 und 1924 für die Krümmungsparameter k = -1 und k = +1, sowie Gesamtdruck p = 0 (also einem Substrat aus Staub). H.P. Robertson fand die flache Lösung mit k = 0 (Euklidisches Universum).
Die Friedmann-Weltmodelle beschreiben Universen konstanter Krümmung k. Räume konstanter Krümmung haben einen Riemannschen Krümmungstensor mit einfacherer Gestalt, als im allgemeinen Fall beliebig gekrümmter Mannigfaltigkeiten.

Drei Krümmungstypen des Kosmos

FLRW-Modelle unterscheiden sich in ihrer globalen Geometrie und Topologie:

• elliptisches oder sphärisches Universum: Krümmung k = +1.
  Dieses Weltall ist geschlossen, unbegrenzt, hat jedoch endliches Volumen. Eine moderne Manifestation dieses Typs ist das Dodekaeder-Universum.
• Euklidisches Universum: Krümmung k = 0.
  Dieses Weltall ist offen/unendlich oder geschlossen/endlich. Das Universum ist flach. Hier gelten die Sätze der ebenen Geometrie Euklids, z.B. die Winkelsumme im Dreieck beträgt 180 Grad. Im Konsens-Modell der Kosmologie (engl. concordance model) ist das unendlich ausgedehnte, flache Universum die Grundlage.
• hyperbolisches Universum: Krümmung k = -1. Das Horn-Universum mit negativer Krümmung ist eine moderne Alternative zum flachen Universum.
  Dieses Weltall ist ebenfalls offen/unendlich oder geschlossen/endlich – je nach Topologie.

Aber beliebige viele Topologietypen des Kosmos

Eine Entscheidung, welche kosmische Topologie vorliegt ist nicht-trivial und Gegenstand der aktuellen, kosmologischen Forschung. Die Aufstellung zeigt, dass nach der Bestimmung des Krümmungsparameters k nur die Geometrie feststeht, jedoch noch nicht die Topologie. Momentan favorisiert man (auch aus Gründen der Einfachheit; vergleiche Ockhams Rasierklinge) ein flaches, offenes Euklidisches Universum. Flachheit folgt aus den Beobachtungen. Der Euklidische Kosmos konkurriert noch mit dem geschlossenen Dodekaeder-Universum oder Horn-Universum, die als Alternativen vorgeschlagen wurde – noch können sie nicht von den Beobachtungsdaten ausgeschlossen werden. Die topologischen Aspekte der Kosmologie werden unter dem Eintrag Topologie profunder erörtert.

kosmische Materie fließt

In der Herleitung der Friedmann-Gleichung geht die Annahme ein, dass das Universum mit Materie, beschrieben als ideale Flüssigkeit, angefüllt ist. Deshalb wurde auch der Energie-Impuls-Tensor einer idealen Flüssigkeit verwendet. Die Flüssigkeit wird durch ihre Energiedichte (relativistische Verallgemeinerung der Massendichte) und ihren Druck p bestimmt. Verschwindet der Druck, p = 0, spricht man von Staub. Die Lösungen der Friedmann-Gleichung werden für verschiedene Parameter diskutiert. Dabei dienen Krümmungsparameter k, kosmologische Konstante ('Lambda', Λ) und Druck der idealen Flüssigkeit p als Klassifikationsmerkmale.

Stars in order of appearance

So folgt eine Klassifikation von Friedmann-Universen in chronologischer Reihenfolge ihrer Entdeckung:

• Bereits 1917 schlug Albert Einstein sein statisches Universum vor. Bei statischen Lösungen ist der Weltradius konstant, R(t) = const. Lambda wurde ja von Einstein auf diese Weise eingeführt und ist ungleich null. Als Krümmung wurde k = +1 gewählt, weil alle sphärischen Universen geschlossen sind, was Einstein als ästhetisch empfand. Im statischen Universum verschwinden sowohl Hubble-Parameter, als auch Abbremsparameter, was anschaulich unmittelbar einsichtig ist.
• Im gleichen Jahr 1917 fand der holländische Astronom Willem de Sitter (1872 – 1934) eine flache Lösung, k = 0, mit positiver kosmologischer Konstante, die dynamisch, aber materiefrei (Energie-Impuls-Tensor null) ist. Damit verstößt sie gegen das Machsche Prinzip! Die Dynamik dieser de-Sitter-Lösung wird von der Dunklen Energie verursacht.
• 1922 schlägt Friedmann die Gleichung vor, die heute nach ihm benannt wurde. Sie enthält sämtliche Universen, auch den statischen Einstein-Kosmos. Die Friedmann-Lösungen im engeren Sinne fand Friedmann 1922 und 1924 selbst. Für sie gilt: verschwindendes Lambda, k = -1,+1 und p = 0. Besonders interessant sind Friedmanns oszillierende Weltmodelle für negative Lambda. Die Dunkle Energie stoppt die Expansion und verursacht eine Kontraktion des Universums. Im Prinzip könnte dieses Universum beliebig oft expandieren und kontrahieren. Es ist ein pulsierendes Universum. Friedmanns Erkenntnisse waren jedoch für die damalige Zeit zu avantgardistisch. Ein dynamisches Universum war jenseits jeder Vorstellung – auch für die Kosmologen der ersten Stunde, allen voran Einstein. Friedmanns Lösungen fanden sehr zögerlich die Akzeptanz anderen Kosmologen.
• Der belgische Kosmologe Abbé Georges Lemaître (1894 – 1966) arbeitete auf gleichem Gebiet wie Friedmann. Er fand 1925 die Lösung eines expandierenden Universums. Zunächst wurden positive Krümmung und positives Lambda vorausgesetzt. Dynamische Universen waren zu dieser Zeit äußerst unattraktiv. Erst Hubbles Entdeckung der Fluchtbewegung der Galaxien im Jahr 1929 verschafften den Friedmann-Lemaître-Modellen verdienten Zulauf.
• 1929 fand Robertson Lösungen mit beliebigem Lambda, k = 0 und p = 0.
• Im Zuge von Einsteins zurückgenommener kosmologischer Konstante, erlangen Modelle mit verschwindendem Lambda zunehmend Aufmerksamkeit. Das Einstein-de-Sitter-Universum (1932) ist flach, k = 0.
• In der Folgezeit wurden viele Subklassifikationen der Friedmann-Lemaître-Lösungen gefunden (nach Robertson, 1933).

Lemaître: Erfinder des Urknalls unter anderem Namen

Dynamische Universen haben variablen Weltradius R(t), der häufig auch als Skalenfaktor a(t) in der Fachliteratur bezeichnet wird. Die Entdeckung der Expansion führte Lemaître zu der Annahme, dass wenn man die Expansion zeitlich zurück extrapoliert, es ein beliebig kleines Universum gegeben haben muss. Lemaître nannte dies die 'Geburt des Raumes' (Artikel in Nature 1931). Demzufolge darf er als der 'Vater der Urknall-Theorie' bezeichnet werden.

Was sind das für Ωs?

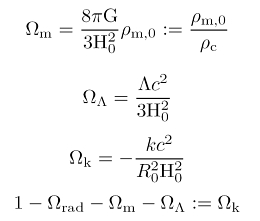Bei der Diskussion der Friedmann-Gleichungen bietet sich an, einige dimensionslose Größen einzuführen: die Dichteparameter. Sie werden symbolisiert durch den letzten Buchstaben des griechischen Alphabets, Ω, der verschiedene Indizes trägt. Die Terme der Friedmann-Gleichung (ganz oben) lassen sich so in eine Summe aus Dichteparametern umschreiben. Jeder Dichteparameter kann einer bestimmten Energieform bzw. Energiedichte zugeordnet werden:

• Materie, zusammenfassend für baryonische Materie und Dunkle Materie,
• Dunkler Energie oder Lambda-Term,
• elektromagnetische Strahlung im Kosmos,
• Krümmungsvorzeichen der globalen Raumzeit.

Die Omegas erhalten entsprechende Indizes, um die Energieform zu charakterisieren (Ω_m: Materie, Ω_Λ: Dunkle Energie, Ω_rad: Strahlung, Ω_k: Krümmung des Universums). Die Omegas hängen im Allgemeinen von der Zeit bzw. von der kosmologischen Rotverschiebung ab! Der Index 0 steht üblicherweise für das lokale Universum, z = 0 ('heute'). Die Friedmann-Gleichung kann mit den Definitionen der Omegas wie sie rechts notiert sind auf Dichteparameter umgeschrieben werden, so dass man die untere Gleichung rechts erhält. Der Astronom misst nun die beispielsweise die Omegas von Strahlung, Materie und Dunkler Energie im lokalen Universum und kann so die Krümmung des Kosmos bestimmen.

Expansion vs. Abbremsung

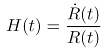Die Dichte-Parameter bestimmen zusammen mit dem Hubble-Parameter und dem Abbremsparameter vollständig die Dynamik des Universums. Man bezeichnet diesen Parametersatz als kosmologische Parameter, weil sie sämtliche Eigenschaften des Kosmos – bis auf die globale Topologie – bestimmen. Der Hubble-Parameter H(t) (siehe Gleichung rechts) ist mit der Expansionsgeschwindigkeit des Universums in der Epoche t assoziiert und im Allgemeinen zeitabhängig (bzw. abhängig von der Rotverschiebung). Im lokalen Universum kann zwischen kosmologischer Rotverschiebung und Entfernung (vergleiche Entfernungsmodul) approximativ eine lineare Beziehung abgeleitet werden: das Hubble-Gesetz. Der amerikanische Astronom Edwin Hubble fand dieses Gesetz bereits 1929 auf der Grundlage von nur 18 Galaxien – eine richtige Interpretation, trotz geringer Datenmenge und schlechter Statistik. Die Proportionalitätskonstante heißt Hubble-Konstante, H₀, und ist nur im nahen Universum konstant. Das lässt sich so verstehen, dass im nahen Universum die Expansionsgeschwindigkeit konstant ist. Bei größeren Distanzen, ab etwa 420 Mpc, bemerkt man Beschleunigungseffekte und die Linearität des Hubble-Gesetzes gilt nicht mehr.

Die Größe der Welt

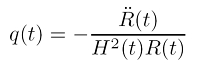Die Größe R(t) bzw. a(t) kann als zeitabhängiger Weltradius verstanden werden. Seine erste Zeitableitung ist assoziiert mit der Expansions- (positives Vorzeichen) oder Kontraktionsgeschwindigkeit (negatives Vorzeichen); seine zweite Zeitableitung ist verknüpft mit der Beschleunigung (positives Vorzeichen) oder Abbremsung (negatives Vorzeichen). Die Gleichung rechts zeigt den so zu definierenden Abbremsparameter q(t) (Brems-, Beschleunigungs-, Dezelerationsparameter oder Dezelerationsfunktion). Der Abbremsparameter charakterisiert die zeitliche Veränderung der Expansionsgeschwindigkeit, also Beschleunigungen der Ausdehnung des Universums. Um dies zu veranschaulichen, skizzieren wir kurz Hubbles historische Technik nach: Hubble maß Rotverschiebungen extragalaktischer Systeme. Aufgrund der kosmischen Expansion streben alle Galaxien auseinander, was sich darin äußert, dass ein Beobachter, der in einem Sternensystem lokalisiert sein mag, die Strahlung aller anderen Galaxien rotverschoben misst. Hubble trug nun seine Daten in einem Diagramm ein: gemessene Radialgeschwindigkeiten über zugehörigen Entfernungen (bestimmt mithilfe der Cepheiden). Im Bereich bis etwa 15 Mpc ergibt sich eine Gerade: das ist das lineare Hubble-Gesetz! Die Steigung der Geraden entspricht der Hubble-Konstanten. Die Auswirkungen von Abbremseffekten sieht man für größere Distanzen beobachteter Systeme. Dann knickt die Gerade nach oben oder nach unten ab. Das parametrisiert nicht die Steigung der Gerade (1. Ableitung), sondern ihre Krümmung (2. Ableitung). Daraus resultiert die Gleichung für den Abbremsparameter. Im Allgemeinen werden Hubble-Parameter und Abbremsparameter für jede Epoche t ausgewertet und die so resultierenden Zeitabhängigkeiten analysiert.

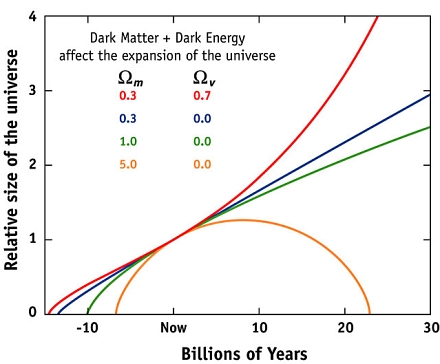
Dynamische Modelluniversen im Vergleich

Die Abbildung oben zeigt unterschiedliche Szenarien, wie sich ein dynamisches Universum entwickeln kann (Credit: WMAP-Website). Auf der horizontalen Achse ist die kosmische Zeit in Einheiten von Milliarden Jahren aufgetragen. Bei der Stelle Now befinden wir uns als lokale Beobachter auf der Erde. Links von Now schauen wir in die Vergangenheit unseres Universums und rechts von Now in die Zukunft. Auf der vertikalen Achse ist die Größe des Universums als Weltradius aufgetragen. Die Einheiten sind willkürlich und wurden so normiert, dass der Weltradius bei Now gerade exakt 1 ist. Im Urknall muss der Weltradius null gewesen sein – hier startet also die Entwicklung des dynamischen Kosmos. Die unterschiedlichen Kurven stehen nun jeweils für ein anderes Friedmann-Weltmodell. Die Parameter, die den Kurvenverlauf und damit das Schicksal des Universums bestimmen, sind die beiden Dichteparameter Ω_m (die 'Materie', d.h normale plus Dunkle Materie) und Ω_V (das 'Vakuum', also die Dunkle Energie). Am Anfang dehnen sich alle Modelluniversen aus, weil zunächst alle Kurven von links unten nach rechts oben ansteigen. Allerdings starten sie an unterschiedlichen Stellen; mit anderen Worten: je nach Energieinhalt haben die Modelluniversen unterschiedliches Alter. Dieses Alter kann man am Kreuzungspunkt der Kurve mit der horizontalen Achse ablesen: die grüne Kurve steht für ein Universum mit einem Alter von 10 Mrd. Jahren; ganz links liegt ein Alter von knapp 15 Mrd. Jahren vor.

erst Expansion, dann Kollaps

Die orangegelbe Kurve zeigt einen besonderen Verlauf: der Weltradius nimmt in der Zukunft (rechts von Now) wieder ab! Betrachten wir die Parameter, so stellen wir fest, weshalb das so ist: dieses Modelluniversum enthält sehr viel Materie (Ω_m = 5.0) und gar keine Dunkle Energie (Ω_V = 0). Die Zahl 5 bedeutet, dass die Materiedichte die kritische Dichte um das Fünffache überschreitet! Dieses Universum enthält soviel Materie, dass irgendwann in der Zukunft (nach knapp weiteren 10 Mrd. Jahren) die Gravitation gewinnt und die Expansion wieder umkehren kann. Als Konsequenz kollabiert das Universum und die kosmologische Rotverschiebung kehrt sich um in einer kosmologische Blauverschiebung. Das ist ein geschlossenes Universum.

kritische Expansion

Die grüne Kurve enthält hingegen etwas weniger Materie (Ω_m = 1.0) und ebenfalls keine Dunkle Energie. Der Materieinhalt entspricht exakt der kritischen Dichte. Wie man sieht, startet die Expansion recht flott, aber die Kurve flacht immer mehr ab, so dass die Expansion immer langsamer wird. Der Materieinhalt reicht hier nicht aus, damit das Universum in sich zusammenfällt.

verlangsamte Expansion

Bei der blauen Kurve liegt die Materiedichte unterhalb der kritischen Dichte (Ω_m = 0.3; ebenfalls keine Vakuumenergie). Es handelt sich um ein offenes Universum, bei dem sich die Expansion verlangsamt, aber aufrechterhalten wird. Im Unterschied zur grünen Kurve ist dieses Modelluniversum älter – die blaue Kurve schneidet die horizontale Achse weiter links, d.h. zu früheren kosmischen Zeiten.

beschleunigte Expansion nur mit Dunkler Energie

Die rote Kurve enthält dieselbe Materiedichte wie die blaue (Ω_m = 0.3), aber zusätzlich gibt es auch Dunkle Energie (Ω_V = 0.7) – verglichen mit der Materiedichte sogar mehr als doppelt soviel. Die Dunkle Energie weist einen negativen Druck auf und wirkt somit antigravitativ. Dieser Effekt wird besonders ausgeprägt zu späten Entwicklungsphasen dieses dynamischen Modelluniversums. Es ist klar zu sehen, dass die Expansion sogar beschleunigt wird – die rote Kurve steigt nach rechts extrem an. Dieser Vorgang kann nur mit der Dunklen Energie als Zutat erklärt werden.
Es sei bei dieser Kurve auf ein besonderes Detail hingewiesen: am Anfang steigt der Weltradius zwar an, aber die Expansion wird für eine Zeit lang abgebremst! Das erkennt man an der Rechtskrümmung der Kurve; später verschwindet das und eine klare Linkskrümmung liegt vor. Zu Beginn der der Expansion war die Dunkle Energie dynamisch noch nicht so relevant. Erst zu späten kosmologischen Epochen hin dominiert sie die Dynamik des ewig expandierenden Kosmos.

Unser beschleunigt expandierender Kosmos

Die Aufgabe der Astronomen ist es nun Beobachtungen durchzuführen, um Datenpunkte in dieses Diagramm eintragen zu können. Versammeln sich die Datenpunkte eindeutig auf einer der Kurven, so steht das Friedmann-Modell für unser Universum fest. Das Sammeln von Datenpunkten übernehmen beispielsweise Supernovaforscher, die weit entfernte Supernovae vom Typ Ia analysieren. Fatalerweise schmiegen sich alle Kurven im Bereich von Now sehr eng aneinander. Die Astronomen müssen demnach tief in die Vergangenheit des Kosmos schauen (dort, wo die Kurven voneinander abweichen), um klar bestimmen zu können, welcher Kurve unser Universum folgt – leider können sie nicht in die Zukunft blicken und Datenpunkte rechts von Now eintragen. Liegt jedoch die Kurve fest, so wissen wir, wie sich das Universum in Zukunft entwickeln wird!
Die Astronomen wissen es. Ende der 1990er Jahre wurde tatsächlich die beschleunigte Expansion anhand von weit entfernten, explodierenden Weißen Zwergen gemessen.

Unser Universum folgt der roten Kurve!

Wir leben in einem Universum, dass nach den aktuellen Erkenntnissen der modernen Kosmologie niemals kollabieren wird, aber ewig expandieren und dabei langsam auskühlen wird. Das Alter unseres Universums beträgt 13.7 Mrd. Jahre – bei dieser Zahl schneidet die rote Kurve die horizontale Achse. Die Zusammensetzung unseres Universums ist so, wie die Parameter der roten Kurve nahe legen: ein Drittel Materie, zwei Drittel Dunkle Energie (s.u. für die präzisen, aktuellen Daten).
Die Supernovadaten passen zu allen anderen astronomischen Messungen (kosmische Hintergrundstrahlung, großräumige Verteilung der Galaxien und Galaxienhaufen, Häufigkeiten der primordialen Elemente) und auch zu den Erkenntnissen aus der Altersbestimmung. So gibt das Alter von Objekten im Kosmos ein Mindestalter für das Universum vor. Die Altersbestimmung mit radiogenen Methoden bei Gesteinen oder das Alter von Kugelsternhaufen (den ältesten Systemen in der Milchstraße) oder von Weißen Zwergen – all das passt zu den Erkenntnissen der experimentellen Kosmologie.

aktuelle Werte der Hubble-Konstanten H₀

• Die Hauptaufgabe des amerikanischen Weltraumteleskops Hubble (Hubble Space Telescope, HST) war es gerade, die Hubble-Konstante äußerst präzise zu messen. Ergebnis: H₀ = 72 km s^-1 Mpc^-1 (H0KP, Freedman et al. 2001).
• Auch die Verteilung der kosmischen Hintergrundstrahlung kann herangezogen werden, um die kosmologischen Parameter zu messen. Brandaktuelles Ergebnis: H₀ = 73 km s^-1 Mpc^-1 (WMAP 3^rd year data, Spergel et al., 2006; astro-ph/0603449).

Auch Astronomen streiten

Zuvor stritten Kosmologen jahrzehntelang, ob die Hubble-Konstante eher bei 50 oder eher bei 100 km s^-1 Mpc^-1 läge. Dieser Streit ist mittlerweile beigelegt, weil die Fehlerbalken aufgrund mehrerer unabhängiger Methoden sehr klein geworden sind.

Rezept für ein Universum

Die Konstituenten kosmischer Energieformen sind aktuell gemäß Messungen des Mikrowellen-Satelliten WMAP (Stand März 2006, Quelle WMAP Homepage), der die Hintergrundstrahlung exakt vermessen hat:

• gewöhnliche, baryonische Materie: 4%
• Strahlung: irrelevant,
• heiße Dunkle Materie (HDM): irrelevant,
• kalte Dunkle Materie (CDM): 22%,
• Dunkle Energie (Lambda): 74%.

Der Beitrag von elektromagnetischer Strahlung kann im lokalen Universum vernachlässigt werden, weil Ω_rad ~ 10^-5 beträgt. Die Strahlung wird durch die Expansion des Kosmos sehr stark ausgedünnt; allerdings war sie in der Frühphase des Universums wichtig – vor allem in der Phase des strahlungsdominierten Kosmos.

Das größte Geheimnis der Astrophysik

Damit kommt der Dunklen Energie die tragende Rolle in der Kosmodynamik des bereits entwickelten Universums zu. Sie macht sich als Antigravitation bemerkbar und treibt die Expansion des Universums. Auch wenn Interpretationen in Form von Vakuumpolarisationen des Quantenvakuums oder ultraleichten skalaren Bosonen wie dem Cosmon oder dem Radion für diese Komponente vorliegen, gehört sie doch zu den größten Geheimnissen des Kosmos.

Moderne Entwicklungen

Die Friedmann-Modelle dienen in der modernen Kosmologie als einfache Modell-Universen. In den 1980er Jahren wurden diese Modelle modifiziert und eine Phase exponentieller Expansion des Universums implementiert. Diese Phase heißt Inflation. Die aktuellen Supernovamessdaten bevorzugen eindeutig die kosmologische Konstante Λ, die man als konstante und gleichmäßig verteilte Form Dunkler Energie ansehen kann. Trotz dieser aktuellen Datenlage haben Physiker zeitlich veränderliche Formen Dunkler Energie wie Quintessenz-Modelle entwickelt. Motiviert ist das durch das Problem der Kleinheit von Λ und das Koinzidenzproblem.
Eine andere moderne Stoßrichtung ist die Berücksichtigung räumlicher Extradimensionen. In diesen Modellen werden neben einer Zeitdimension und drei Raumdimensionen, die in der Raumzeit der ART verknüpft sind, weitere räumliche Dimensionen angenommen, die möglicherweise kompaktifiziert sind. Diese Ansätze modifizieren das klassische vierdimensionale Linienelement der ART. Solche Überlegungen folgen vor allem aus den Stringtheorien. Diese neuen Ansätze resultieren in einer Kosmologie mit Branen, zum Beispiel realisiert als ADD-Szenario, DGP-Szenario oder Randall-Sundrum-Modelle. Wenn räumliche Extradimensionen existieren sollten, wird die klassische Friedmann-Gleichung der vierdimensionalen Kosmologie deutlich modifiziert. Es gibt dann neue Terme, die von der Spannung der Bran oder von der Dunklen Strahlung (engl. dark radiation) abhängen. Außerdem skaliert der Hubble-Parameter bei hohen Energien linear mit der Energiedichte (klassisch steigt er nur mit der Wurzel an).
Diese Modelle mit neuer Physik haben attraktive Eigenschaften – letztendlich muss aber die Naturbeobachtung klären, ob die Modelle etwas mit der Realität zu tun haben.

Weitere Literatur

• Buchtipp: Einführung in die Kosmologie von Hubert Goenner (1994), Spektrum Verlag
• Vortrag: An introduction to Brane World Cosmology (Stand März 2004).