Eine Bran (engl. brane), genauer gesagt eine p-Bran, ist gemäß der Stringtheorien ein schwingungsfähiges Objekt mit der Dimension p. Die Bezeichnung geht auf Paul Townsend zurück und ist an das Wort Membran (engl. membrane) angelehnt.

Branen haben unterschiedliche Dimension

Brane sind Verallgemeinerungen von Strings, die historisch zuerst gefunden wurden. Daraus resultierte auch etymologisch der Name Stringtheorien. Die Dimension p legt verschiedene Objekte fest. Ist p = 0, so handelt es sich um ein Punktteilchen (0-Bran), p = 1 entspricht einem eindimensionalen Faden, dem eigentlichen String (oder 1-Bran), bei p = 2 handelt sich um eine zweidimensionale Fläche (2-Bran), die man Membran nennt. Ebenso gibt es noch höherdimensionale Branen, 3-Branen etc.

Branen als Teilchen oder als Schwarzes Loch

Die Branen repräsentieren die uns bekannten Teilchen des Standardmodells und darüber hinaus viele, die noch nicht entdeckt wurden, insbesondere wenn Branen in der Supersymmetrie (SUSY) betrachtet werden. Von einem übergeordneten Standpunkt sollten die p-Branen endlich Demokrits postulierten 'Atome' (atomos, grch.: 'unteilbar'), den unteilbaren, fundamentalen Konstituenten der Materie, entsprechen. Branen können aber auch ganze stellare Objekte, wie klassische Schwarze Löcher beschreiben. Branen dienen als Verallgemeinerung des punktförmigen Schwarzen Loches: dieses identifiziert man gerade mit einer 0-Brane. Die erste Generalisierung als 1-Brane nennt man Schwarzen String (engl. black string), die zweite als 2-Brane heißt Schwarze Brane (engl. black brane). Je nach angenommenen Wirkungsfunktional bzw. Lagrangedichte (Einstein-Hilbert-Lagrangian, Einstein-Maxwell-Lagrangian etc.) kann man Branen-Verallgemeinerungen der klassischen Schwarzschild-Lösung (ungeladen, statisch), Reissner-Nordstrøm-Lösung (geladen, statisch) oder Kerr-Newman-Lösung (geladen, rotierend) auffinden.

Auch Strings halten den Rand

Bei offenen Strings kann man Randbedingungen an dessen Enden stellen und sie in bestimmter Weise fixieren. Analog zur Dirichlet-Randbedingung in der klassischen Elektrodynamik nannten die Stringtheoretiker sie daher D-Branen.
Bei den Dp-Branen sind die Enden des Strings auf einer oder möglicherweise verschiedenen p-dimensionalen D-Branen lokalisiert.
Schließlich bezeichnet die M-Brane die Branen der M-Theorie, die sich aus Strings (1-Branen) und p-Branen konstituieren.

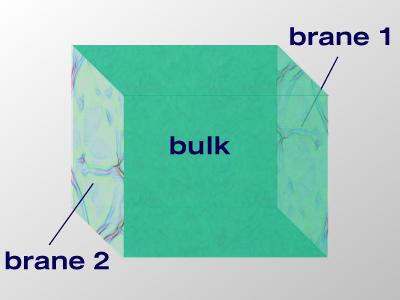
Ein ganzer Kosmos auf der Bran

Das theoretische Konzept mit Branen nennt man umfassend als Branenwelt (engl. brane world) oder auch Brane World Scenario. Dieser Formalismus hat alle Stringtheorien durchdrungen. In der Branen-Kosmologie werden die Branen im Rahmen der relativistischen Kosmologie angewendet und erweitern deutlich die Konzepte der (vierdimensionalen) Standardkosmologie. Wie von den Stringtheorien gefordert, wird die Existenz von Extradimensionen angenommen. Die Branen sind typischerweise dreidimensional (3-Bran) und bilden Hyperflächen im höherdimensionalen Bulk (engl., gesprochen 'balk'). Die Branen können auf dieser Bulk-Geometrie statisch fixiert sein, wie in den Randall-Sundrum-Modellen oder durch die Vermittlung eines Skalarfeldes gegeneinander schwingen. Diese Branendynamik kommt durch die Wechselwirkung mit dem Bulk-Skalarfeld zustande. Im Ekpyrotischen Szenario und dem Zyklischen Universum heißt dieses Feld Radion. Die Dynamik geht dabei soweit, dass die Branen kollidieren können, was kosmologisch mit dem Urknall interpretiert wird. Damit liefern Ekpyrosis und Zyklisches Modell erstmals eine Ursache für den Big Bang. Der Grund sei nichts weniger gewesen, als eine Weltenkollision!

Vortrag im Wissensportal

• Eine Einführung in die Kosmologie mit Branen: An introduction to Brane World Cosmology, Stand März 2004.