Dieser Begriff wurde vor allem durch die Stringtheorien wieder populär, hat jedoch schon weit ältere Wurzeln in physikalischen Theorien. Im Allgemeinen verstehen Physiker unter diesem Begriff weitere räumliche Dimensionen, neben den bekannten drei Raum- und der einen Zeitdimension.

Die Anfänge des Extraraums

Raum und Zeit sind uns vertraut, weil wir uns täglich darin bewegen. Es gibt keinen Zweifel daran, dass diese vier Dimensionen existieren. Als vierdimensionale Raumzeit sind diese Dimensionen Gegenstand der Allgemeinen Relativitätstheorie (ART). Sie bilden in Einsteins ART ein Kontinuum, das Krümmung und Dynamik aufweisen kann. Einsteins Theorie ist eine (unquantisierte) Gravitationstheorie, die über die Newtonsche Gravitation hinausgeht und insbesondere die starke Schwerkraft und kompakte Massen die Natur beschreibt.
Höherdimensionale Räume sind in der Mathematik und der theoretischen Physik nichts Ungewöhnliches. Als Beispiel mögen Funktionenräume dienen, deren Dimension sogar unendlich sein kann. Eine der ersten vereinheitlichten Theorien in der Physik überhaupt ist die Kaluza-Klein-Theorie. Sie wurde bereits in den 1920er Jahren entwickelt, weil die Physiker Relativitätstheorie und Elektromagnetismus in einem einzigen Konzept beschreiben wollten. Neu war der Ansatz, weil Kaluza und Klein eine weitere, neue Raumdimension in dieser Feldtheorie einführten. Der Ansatz setzte sich jedoch nicht in der Physik durch, weil sich die etwa gleichzeitig entwickelte Quantentheorie als erfolgreicher zeichnete.
Erst durch die Fortschritte in den Stringtheorien erlebten die Extradimensionen wieder eine Renaissance: I. Antoniadis sagte Anfang der 1990er Jahre Extradimensionen in den perturbativen Stringtheorien voraus. Im Ansatz sind die Felder des Standardmodells (SM-Felder) auf einen Raum kleinerer Dimension, der so genannten 3-Bran, beschränkt. Die Bran ist jedoch in eine höherdimensionale Welt inklusive Extradimensionen, dem so genannten Bulk, eingebettet. Im Modell wird nun angenommen, dass die Gravitation in alle Raumdimensionen – auch den Extradimensionen – vorzudringen vermag. Damit ist die Schwerkraft in diesem Sinne unbeschränkt, während die SM-Felder nur auf der Bran existieren können (siehe Illustration nach M. Cavaglia, hep-ph/0210296).

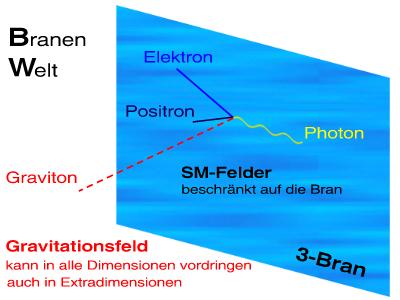
Dieses Modell erklärt das bislang nicht verstandene Beobachtungsphänomen, dass die Gravitation gegenüber den anderen Naturkräften so schwach ist. Dieser als Hierarchieproblem bezeichnete Sachverhalt wird mit der Hypothese von zusätzlichen Raumdimensionen gelöst. Anschaulich gesprochen ist der schnellere Abfall der Gravitationskraft dadurch zu verstehen, dass sie sich in alle Dimensionen ausbreitet. Im Feldlinienbild werden die 'Feldlinien ausgedünnt': die Gravitationskraft wird schwächer auf Skalen, wo die Extradimensionen relevant werden.

Wie misst man weitere Dimensionen?

Offensichtlich tritt der Extraraum im Alltag nicht in Erscheinung. Wenn es die Extradimensionen gibt, so müssen sie auf kurze Abstände beschränkt sein. Diese Erscheinung wird in der Physik Kompaktifizierung genannt und geht in der Grundidee schon auf die Kaluza-Klein-Theorie zurück. Aber wie groß sind die typischen Abstände, bei denen die Extradimensionen physikalisch wichtig werden?
Um diese Frage zu beantworten, versuchen die Physiker den Nachweis der zusätzlichen Raumdimensionen zu erbringen. Das Messprinzip ist eigentlich ganz einfach: Die Modelle mit kompaktifizierten Extradimensionen fordern, dass die Gravitation in den Zusatzdimensionen wirkt. Es ist also zu erwarten, dass bei Erreichen der kritischen Längenskala Abweichungen vom Newtonsche Gravitationsgesetz auftreten. Die Newtonsche Kraftgesetz besagt, dass die Schwerkraft mit dem Abstandsquadrat abnimmt. Es ist ein r^-2-Abstandsgesetz. Rechnerisch kann man zeigen, dass in Modellen mit kompaktifizierten Extradimensionen ein Gravitationskraftgesetz folgt, das bei kleinen Abständen mit höherer Potenz (z.B. r^-4) abfällt. Die genaue Form der Abweichungen hängt davon ab, wie viele Extradimensionen tatsächlich vorhanden sind und auf welcher Längenskala sie kompaktiziert sind. Dieser kritische Abstand heißt in der Literatur Kompaktifizierungsradius. Ist der Kompaktifizierungsradius relativ groß, d.h. groß im Vergleich zu den Abständen, wo die schwache Kraft wirkt – etwa 0.1 Femtometer – , so nennen die Physiker die Extradimensionen große Extradimensionen (engl. large extra dimensions, LED oder LXD). Für große Extradimensionen gibt es bislang keine experimentellen Hinweise – im Gegenteil: wenn es sie gibt, so sind sie auf extrem kleine Abstände 'zusammengerollt'.

Tabletop-Experimente & Mega-Projekte

Die Physiker verwenden ganz unterschiedliche Versuchsanordnungen, um Abweichungen vom Newtonsche Gesetz und damit die Extradimensionen zu beweisen:
Eine Möglichkeit besteht in Experimenten, die der historischen Anordnung des britischen Physikers Henry Cavendish (1731 – 1810) ähneln: Dazu verwendet man ein so genanntes Torsionspendel (auch Drehwaage, Gravitationswaage genannt). Dies ist ein hantelförmiges Gebilde aus zwei Metallkugeln, die an einem Draht aufgehängt werden. Diese frei bewegliche Anordnung wird von zwei weiteren, schweren Kugeln über Gravitationskräfte in eine Drehschwingung (Torsionsschwingung) versetzt. Aus der Verdrillung des Drahtes und der Schwingung kann bei bekannter Gravitationskonstante die Massen bestimmen oder aus bekannten Massen der Kugeln die Gravitationskonstante, oder man kann auch die Gültigkeit des Newtonschen Kraftgesetzes und dessen Abnahme mit dem Abstandsquadrat testen. Bisher konnten mit solchen Cavendish-Experimenten keine Extradimensionen nachgewiesen werden – vermutlich deshalb, weil der Kompaktifizierungsradius viel kleiner ist, als der kleinstmögliche Abstand der Kugeln – oder weil es Extradimensionen nicht gibt.
In einer völlig anderen Versuchsanordnung werden nicht makroskopische Kugeln, sondern ultrakalte Neutronen verwendet. Grundlage dieses Experiments ist der Einschluss von Neutronen zwischen Platten. Die gesamte Anordnung ist dem Gravitationsfeld ausgesetzt. Die Neutronen haben eine Ruhemasse und fallen daher im Gravitationsfeld wie alle Testmassen. Allerdings werden in solchen Experimenten, wo Neutronen über einem Neutronen reflektierenden Spiegel fallen, Quanteneffekte wichtig: Die Neutronen fallen nicht kontinuierlich, sondern nehmen dabei diskrete Zustände ein, die von der Quantenmechanik diktiert werden. Die im Gravitationsfeld gebundenen Zustände der Neutronen können benutzt werden, um die Gültigkeit des Newton-Gesetzes im Mikrometerbereich anzugeben. Als Ergebnis konnte die Gültigkeit des klassischen Newtongesetzes in einem Fenster im Bereich von 1 bis 10 Mikrometern bestätigt werden (Abele et al., Lect. Notes Phys. 631, 355, 2003; Preprint hep-ph/0301145).
Der verbleibende Bereich für Kompaktifizierungsradien, der noch nicht experimentell untersucht wurde, liegt demnach zwischen der Millimeter- und der Mikrometerskala. Mittlerweile liegen auch für diesen Bereich Untersuchungen vor, die das Newton-Gesetz bestätigen und damit die Existenz von Extradimensionen bis hinunter in den Mikrometerbereich widerlegen. In diesen neuen Experimenten messen Physiker die Anziehung zwischen zwei Metallscheiben infolge der Gravitationskraft. Der Scheibenabstand kann vom Millimeter- bis in den Mikrometerbereich variiert werden. Das aktuelle Ergebnis ist, dass der Kompaktifizierungsradius der Extradimensionen kleiner ist als 44 Mikrometer (Kapner et al., Phys. Rev. Lett. 98, 021101, 2007; Preprint hep-ph/0611184).
Wie kann man das Gravitationsgesetz auf noch kleineren Abständen untersuchen? Das funktioniert beispielsweise mit Teilchenbeschleunigern. In den Beschleunigungsanlagen der neusten Generation versuchen die Experimentatoren in hochenergetischen Stößen von Protonen oder schweren Ionen in einem extrem kleinen Volumen soviel Energie zu deponieren, dass dieser Bereich zu einem Schwarzen Loch kollabiert! Gemäß der Modelle wären sie um ein Vielfaches leichter (~ 1 TeV) als ihre kosmischen Pendants und hätten nur eine kurze Lebensdauer (typisch 10^-23 Sekunden), wie Berechnungen ergeben haben. Zum Akkretieren wären sie zu kurzlebig, als dass sie eine Gefahr für den Beschleuniger oder gar die Erde darstellen könnten. Denn nach kurzer Zeit würden sie durch die Emission von Hawking-Strahlung zerstrahlen. Die Beobachtung des Zerfalls dieser Mini-Löcher und derer Folgeprodukte würde eine Zählung der Extradimensionen erlauben. Denn es existieren Modellrechnungen unter Annahme verschiedener Dimensionalität der Extradimensionen. Eine signifikante Anzahl von Extradimensionen würde die fundamentale Planck-Skala von 10¹⁹ GeV in den Bereich von nur einigen TeV, der elektroschwachen Skala, herabsetzen. Die damit assoziierte Quantengravitation nennt man TeV-Quantengravitation. Sie könnte demnach bereits bei den neusten Beschleunigertypen wie dem Tevatron in den USA oder dem LHC am CERN studiert werden, sollte es Extradimensionen geben. Es klingt abenteuerlich, aber in den Extradimensionen könnten Gravitonen (nur sie können die 3-Bran verlassen) verschwinden und Energie in andere Dimensionen tragen. Auf diese Weise sollten Extradimensionen in Beschleunigerexperimenten auffallen, weil ab einer kritischen Energie der Energiesatz (scheinbar) verletzt würde (engl. missing-energy experiments). Dabei bestimmt die Anzahl der Extradimensionen die Energieskala (oder äquivalent den Abstand), ab der diese Phänomene auftreten sollten.

Mehr Dimensionen lösen Probleme in der Kosmologie

Die Extradimensionen sind vitale Zutat der moderner, physikalischer Feldtheorien, weil Stringtheorien, M-Theorie und Supergravitationnicht ohne Zusatzdimensionen auskommen. Diese höherdimensionale Branenwelt resultiert letztendlich aus diesen Konzepten und wurde zu einer wichtigen, neuen Stoßrichtung der modernen, relativistischen Kosmologie. Die neuen Modelle sind sehr mächtig: Im ADD-Szenario, den Randall-Sundrum-Modellen, dem DGP-Szenario, dem Ekpyrotischen Szenario und dem Zyklischen Universum finden sich verschiedene Ansätze der Branen-Kosmologie, die mit nicht-kompaktifizierten und kompaktifizierten Extradimensionen operieren. Mit diesen Modellen kann das Wesen der Dunklen Energie neu gedeutet, der Wert der kosmologischen Konstante abgeleitet, der Verlust der Konstanz von fundamentalen Naturkonstanten (Gravitationskonstante, Feinstrukturkonstante) skizziert oder eine Erklärung für den Urknall formuliert werden.

Newtons Nachfahren

Eine andere Theorie, die Abweichungen vom klassischen Newton-Gesetz voraussagt, ist die MOND-Theorie (MOND ist ein Akronym für MOdified Newtonian Dynamics). Hier werden jedoch keine Zusatzdimensionen gefordert, sondern das Kraftgesetz wird beschleunigungsabhängig.

Übrigens, Trekkies:

Den Unterraum, den die kompaktifizierten Extradimensionen aufspannen, kann man als Subraum bezeichnen.