Eine der vier fundamentalen Wechselwirkungen der unbelebten Natur neben gravitativer, schwacher und starker Wechselwirkung.

Maxwells große Entdeckung

In der historischen Retrospektive wurden Elektrostatik und Magnetismus zunächst als separate Phänomene wahrgenommen, bis der englische Physiker James Clerk Maxwell (1831 – 1879) die klassische Elektrodynamik begründete. Seine Maxwellschen Gleichungen – je nach Formulierung vier Differential- oder vier Integralgleichungen – koppeln magnetische an elektrische Felder. Damit konnten elektrische Ströme, Magnetfelder von stromdurchflossenen Leitern, elektrische Felder von elektrischen Ladungen, aber auch elektromagnetische Wellen im Vakuum oder in Medien (Licht) erstmals rechnerisch behandelt werden und als elektromagnetische Effekte verstanden werden.

Vektoranalysis: div, grad, rot

Der mathematische Apparat der klassischen Elektrodynamik umfasst die Vektoranalysis, die Potentialtheorie und die Theorie Greenscher Funktionen. Der Nabla-Operator ist der zentrale Differentialoperator, der die Maxwell-Gleichungen kompakt mithilfe von Gradient (grad), Divergenz (div) und Rotation (rot) schreiben lässt. In der folgenden Abbildung sind von oben nach unten Gradient eines Skalarfeldes, Divergenz eines Dreiervektors, Rotation eines Dreiervektors in kartesischen Koordinaten dargestellt (für andere Koordinatensysteme wie Kugelkoordinaten nehmen die Gleichungen eine andere Form an).

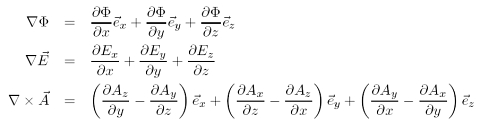
Gaußscher und Stokesscher Satz

Der Nabla-Operator ist nichts anderes als eine gewöhnliche räumliche Ableitung. Die äquivalenten Maxwell-Gleichungen in integraler Form erhält man durch Anwendung der bekannten Integralsätze nach Gauß und Stokes: Der Gaußsche Satz verwandelt ein Volumenintegral der Divergenz eines Vektorfeldes in einer Oberflächenintegral über das Vektorfeld. Der Stokessche Satz verwandelt das Oberflächenintegral über die Rotation eines Vektorfeldes in ein Kurvenintegral des Vektorfeldes entlang der Kurve, die die Oberfläche einschließt.

Maxwell-Gleichungen in differentieller Form

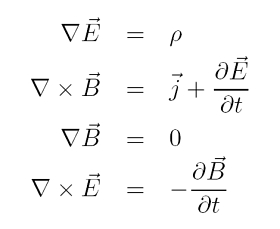In der Abbildung links sind nun alle vier inhomogenen zeitabhängigen Maxwell-Gleichungen im Vakuum in differentieller Form notiert. Die erste und dritte Gleichung machen eine Aussage über die Quellen des elektrischen bzw. magnetischen Feldes. Die erste Gleichung besagt, dass die Quelle des elektrischen Feldes eine elektrische Ladungsdichte ist. Knapp gesagt: Elektrische Ladungen erzeugen ein elektrisches Feld im Raum.. Bei magnetischen Feldern gibt es keine zugehörigen 'magnetischen Ladungen'. In knapper Form heißt es: Es gibt keine magnetischen Monopole.. Die zweite Gleichung nennt man Ampèresches Gesetz. Physikalisch bedeutet es, dass ein stromdurchflossener Leiter mit elektrischer Stromdichte j ein Magnetfeld im Raum induziert. Gleiches passiert, wenn sich ein elektrisches Feld zeitlich ändert. Die letzte Gleichung heißt Faradaysches Induktionsgesetz. Dies wird so interpretiert, dass ein zeitlich variierendes Magnetfeld einen elektrischen Strom in Leitern induziert.
Bei ohmschen Leitern gilt insbesondere das Ohmsche Gesetz: die elektrische Stromdichte ist proportional zum elektrischen Feld, wobei die Proportionalitätskonstante elektrische Leitfähigkeit heißt. Diese Leitfähigkeit ist in ohmschen Leitern unabhängig vom angelegten elektrischen Feld. Vektoriell gesehen sind Stromdichte und elektrisches Feld dann kollinear: die Vektoren ('Pfeile') zeigen in dieselbe Richtung.

klassische Elektrodynamik und Spezielle Relativitätstheorie

Die Maxwell-Theorie ist bereits kovariant, d.h. forminvariant in der Speziellen Relativitätstheorie. Relativistisch betrachtet macht es keinen Sinn zwischen elektrischem und magnetischem Feld zu unterscheiden, weil beide Phänomene äquivalent sind und nur vom Bezugssystem oder Beobachter abhängen! Das lässt sich leicht an folgendem Beispiel nachvollziehen: Ein reines elektrisches Feld einer ruhenden Ladung wird durch Anwendung einer Lorentz-Transformation zu einem Magnetfeld einer bewegten Ladung. Dieser Sachverhalt rechtfertigt in tiefsinniger Weise die Wortsynthese zum Begriff Elektromagnetismus.

Maxwells Theorie häppchenweise

Mit dem Aufkommen der Quantentheorie Anfang des 20. Jahrhunderts wuchs das Bestreben die Maxwell-Theorie zu quantisieren. Im Wasserstoff-Problem tauchte bereits das Photon auf, das bei elektronischen Übergängen in der Atomschale emittiert oder absorbiert wird. Jede Atomschale ist gerade mit Elektronen bestimmter Energie besetzt. Bei einem Quantensprung eines Elektrons wird ein Photon charakteristischer Energie frei oder eingefangen. Die elektromagnetische Welle, die man in Form einer Wellengleichung aus den Maxwell-Gleichungen ableitet, ist jedoch noch unquantisiert. Der Quantisierungsapparat ermöglicht eine Umformulierung der klassischen Wellengleichung mithilfe von Feldoperatoren. Auf diese Weise erhält man die Klein-Gordon-Gleichung. Die daraus entstandene Quantenelektrodynamik (QED) war die erste erfolgreiche Quantenfeldtheorie überhaupt. Das Renormierungsverfahren wurde ebenfalls an der QED entwickelt. Der mathematische Apparat der Quantenfeldtheorie ist die Gruppentheorie. Eine U(1)-Theorie beschreibt hier die photonischen Wechselwirkungen. Da das Photon keine Ruhemasse aufweist, ist seine Reichweite unendlich. Die wesentlichen Wechselwirkungen in makroskopischen, kosmischen Dimensionen und insbesondere in der Astrophysik sind daher Elektromagnetismus und Gravitation. Die anderen Wechselwirkungen werden erst wichtig, wenn das Universum extrem klein ist und die Ausdehnung vergleichbar wird mit dem subatomaren Bereich. Dieser mikroskopische Bereich ist gerade in der Gegend der Planck-Skala. Ein mikroskopisch kleiner Zustand des Kosmos hat kurz nach dem Urknall vorgeherrscht und tangiert dann das Regime der Planck-Ära, der Großen Vereinheitlichten Theorien (GUT) bzw. Vereinheitlichten Theorie (UT).

Vereinheitlichung der Naturkräfte

Das Unifikationsbestreben fand im Elektromagnetismus jedoch erst seinen historischen Anfang (sieht man einmal von Sir Isaac Newton ab, dem die Vereinheitlichung von irdischen und kosmischen Kräften zugeschrieben wird). Mittlerweile ist es gelungen, die schwache und elektromagnetische Wechselwirkung in der elektroschwachen Theorie zu vereinigen. Hier wurde eine enge Verwandtschaft von Photon und Weakonen offen gelegt, die bei hohen Energien betrachteter Teilchenprozesse als eine elektroschwache Kraft behandelt werden können. Der nächste Schritt sind die Großen Vereinheitlichten Theorien, die die starke Kraft im Rahmen einer SU(5)-Theorie zur Elektroschwachen Kraft hinzunehmen. Ab 10¹⁶ GeV Energie fordern die Teilchenphysiker neue Eichbosonen: die X-Bosonen und Y-Bosonen (zusammengefasst als Leptoquarks). Der letzte Schritt ist der schwierigste und noch nicht vollzogen worden: die Gravitation kann noch nicht vollständig mit quantenfeldtheoretischen Konzepten beschrieben werden. Deshalb steht eine Vereinheitlichung aller vier Naturkräfte als Vereinheitlichte Theorie (engl. Unified Theory, UT) oder eine Theorie von Allem (engl. Theory Of Everything, TOE) noch aus. Ein diskutierter Kandidat in dieser Hinsicht sind die Stringtheorien.