Ray Tracing, dt. 'Strahlenverfolgung', ist eine Methode, um Objekte in 2D oder 3D zu visualisieren. Dabei wird die Ausbreitung von Licht simuliert und – im Idealfall – alle Wechselwirkungen der Strahlung (Reflexion, Brechung, Streuung) mit den Objekten im betrachteten Gebiet berücksichtigt.

Licht auf Geraden

Kommerzielle Ray-Tracer-Software, z.B. 3D-Computerspiele oder CAD-Software, arbeitet in der flachen Raumzeit, wie es Relativisten ausdrücken würden. D.h. es liegt der gewöhnliche Grenzfall der geometrischen Optik vor: Licht bewegt sich entlang von Geraden. Eigentlich ist das jedoch ein Spezialfall.

Licht geht in die Kurve

Ganz allgemein besagt die Allgemeine Relativitätstheorie (ART) von Albert Einstein, dass Masse und Energie die Raumzeit krümmen. Um nun die Ausbreitung von Licht zu verfolgen, müssen die Geodäten der Lichtteilchen berechnet werden. Diese 'Lichtbahnen' heißen in der ART Nullgeodäten. Im Allgemeinen sind die Lichtbahnen gebogen, weil auch der 'Raum krumm ist'. Etwas schicker formuliert: Nullgeodäten folgen der gekrümmten Raumzeit.

Wie kommt man auf die Lichtbahnen in der ART?

Zunächst muss man wissen, in welcher Raumzeit sich das Licht ausbreitet. Ist es das Gravitationsfeld der Sonne oder die Umgebung eines Neutronensterns oder soll sogar gezeigt werden, wie ein Schwarzes Loch Licht verschluckt? Sobald das geklärt ist, formuliert man mit der nun bekannten Metrik der Gravitationsquelle die so genannte Nullgeodätengleichung: das ist nichts anderes als die voll relativistische Bewegungsgleichung für Lichtteilchen (die Ruhemasse null haben). In Gestalt einer Geodätengleichung verraten sich auch die Teilchenbahnen für Teilchen mit Ruhemasse. In jedem Fall ist die Geodätengleichung mathematisch gesprochen eine Differentialgleichung zweiter Ordnung.

Ein Lichtteilchen macht noch kein Bild...

...zumindest kein aufregendes. Die Nullgeodätengleichung muss daher für viele Lichtteilchen, die unterschiedliche Startbedingungen (Startposition, Strahlrichtung) haben, gelöst werden. 'Von Hand' wäre das eine mühevolle Prozedur, weil erst etwa eine Million Lichtteilchen (ein Bild mit 1000 × 1000 Pixel) ein aussagekräftiges und aufregendes Bild macht. Deshalb benutzt man natürlich Computer zur Berechnung des Bildes – Fachleute nennen das (sowohl in flachen, als auch gekrümmten Raumzeiten) auch Rendern.
Bei dieser Rechnung muss auch klar sein, wo der Beobachter der Szenerie ist. Denn die Geodätengleichung verknüpft ja einen Lichtstrahl von seiner Startposition mit einem Auftreffpunkt. Wo der Auftreffpunkt liegt diktiert einerseits der Lichtstrahl durch seine Startbedingungen und andererseits die Metrik mit ihrer Krümmung.
Das ganze Verfahren von der Berechnung der Lichtausbreitung in gekrümmten Raumzeiten wird nun allgemein relativistisches Ray Tracing (engl. general relativistic ray tracing) genannt. Es gibt auch speziell relativistisches Ray Tracing, das ausrechnet, wie die Umwelt ausschaut, wenn man sich fast mit Lichtgeschwindigkeit durch eine Szenerie bewegt.

Lichtausbreitung nahe eines Schwarzen Loches

Betrachten wir doch gleich einen Extremfall und zwar die Bewegung von Lichtteilchen in der Umgebung eines Schwarzen Loches. Die Raumzeit, die benutzt werden muss, ist entweder die Schwarzschild-Metrik (Loch rotiert nicht) oder die etwas kompliziertere Kerr-Metrik (Loch rotiert). Die folgende Abbildung skizziert, was berechnet werden soll: ein Lichtstrahl (engl. ray) startet von einer dünnen Scheibe (engl. thin disk), die um ein Schwarzes Loch (engl. black hole) rotiere (z.B. eine Standardscheibe) und bewege sich durch die gekrümmte Raumzeit (engl. curved space-time). Der Beobachter möge weit entfernt vom Loch sitzen, wo die Raumzeitkrümmung des Loches vernachlässigbar ist (asymptotisch flache Raumzeit). Der Beobachter betrachtet in diesem Fall ein Bildschirm (engl. camera screen), auf dem das Bild abgebildet werden soll.

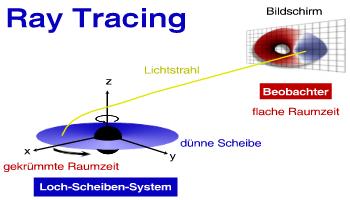
Für jedes Pixel des Bildes muss die Geodätengleichung gelöst werden. Hier bedient man sich aus numerischen Gründen einer nützlichen Eigenschaft von Licht: Lichtwege sind umkehrbar. Es wäre unnötig die Bahnen sämtlicher Lichtteilchen zu rechnen, die von der Scheibe starten, weil nur ein Bruchteil von ihnen am Bildschirm ankommt. Wir sind doch nur an dem Bild auf dem Bildschirm interessiert. Also machen wir es lieber umgekehrt und 'rechnen rückwärts' (back tracking): die Berechnung startet am Bildschirm und je nachdem, ob das Teilchen die Scheibe, das Loch oder nichts trifft, wird es eingefärbt. Schwups, fertig ist das Bild.

zwei Rechenverfahren

• Die Geodätengleichung kann erstens durch direkte Integration gelöst werden, was numerisch aufwendiger ist und höhere Rechnerleistungen erfordert. Dieses Verfahren hat den Vorteil, dass es für beliebige Raumzeiten funktioniert.
• Die Geodätengleichung kann zweitens durch Integrale der Bewegung (Erhaltungsgrößen) gelöst werden, was numerisch effizient und schnell ist. Der Vorteil ist hier, dass deutlich weniger Computerleistung nötig ist.

Lösung der Geodätengleichung mit Erhaltungsgrößen

Im Falle eines Schwarzschild- oder Kerr-Loches nutzt man die Kenntnis von vier Erhaltungsgrößen des Systems aus. Neben Masse, Energie und Drehimpuls ist die wesentliche Größe in der Kerr-Geometrie (die ja Schwarzschild als Spezialfall enthält) die Carter-Konstante. Brandon Carter leitete 1968 diese neue Bewegungskonstante aus der Separabilität der Hamilton-Jacobi-Gleichung ab. Diese vierte Erhaltungsgröße ist ein exklusives Merkmal der Kerr-Metrik und fehlt bei anderen achsensymmetrischen Raumzeiten, wie beispielsweise bei Neutronensternen.

Einsteins verzerrte Welt

Der berechnete Verlauf der Nullgeodäten dient also der Herstellung voll relativistischer Bilder: Auf dem Bildschirm sieht der Betrachter Bilder, die mit Einsteins Theorie als Methode und einem Pinsel aus Licht gemalt wurden. Und was man da sieht ist ganz erstaunlich! Die relativistische Welt sieht vollkommen anders, asymmetrisch und verzerrt aus:

• Das Objekt, das leuchtet, stellt sich im Allgemeinen verzerrt und verbogen, manchmal sogar mehrfach dar. Das ist ein Resultat des Gravitationslinseneffekts.
• Falls sich die Lichtquelle auf den Beobachter bewegt, gibt es Blauverschiebungseffekte; falls sich die Lichtquelle vom Beobachter entfernt, so ist es eine Rotverschiebung. Beides wird zusammengefasst im Doppler-Effekt.
• Natürlich tritt auch das Loch selbst in Erscheinung: schwarz, wie es sich gehört. Der physikalische Grund ist, dass Lichtteilchen, die am Ereignishorizont starten oder ihm zu nahe kommen, vom Loch verschluckt werden. 'Verschlucktes Licht' ist schwarz. Dieser Effekt heißt Gravitationsrotverschiebung.

Das Resultat eines relativistischen Ray Tracing zeigt die Abbildung rechts. Es handelt sich im Prinzip um ein Falschfarbenbild, bei dem die Helligkeit einer Gasscheibe farbkodiert wurde: geringe Helligkeit ist schwarz und hohe Helligkeit weiß dargestellt; Zwischenwerte sind gelb. So sieht demnach eine dünne, gegen den Uhrzeigersinn rotierende Scheibe aus, die sich um ein ebenfalls rotierendes Schwarzes Loch dreht. Bei der Scheibe wurde angenommen, dass man fast auf ihre Kante blickt: die Neigung beträgt 70°. Die Scheibe sieht verzerrt aus, als ob sie von hinten nach oben gebogen wurde. Das ist gerade der Gravitationslinseneffekt. Wie man sieht, ist die Strahlung, die vom linken Teil der Scheibe kommt heller, als der recht Teil. Das ist der oben angesprochene Doppler-Effekt, der sich ja nicht nur in der Lichtfarbe (=Strahlungsenergie), sondern auch in der Helligkeit (=Strahlungsfluss) bemerkbar macht. Das Loch selbst ist hier zum besseren Erkennen weiß dargestellt worden: aus diesem Bereich kommt jedoch kein einziges Lichtteilchen. Das ist der Ereignishorizont des Schwarzen Loches.

Nutzen für die Astrophysik

Die gerenderten Bilder haben einen enormen Informationsgehalt und bieten viel Anlass zur wissenschaftlichen Diskussion. In der Natur ist die Umgebung eines Schwarzen Loches leider noch nicht so fotografiert worden. Das liegt daran, weil die Auflösung der Teleskope dazu (noch!) nicht ausreicht. Die kosmischen Schwarzen Löcher sind zu kompakt und zu weit entfernt, als dass diese Fotos zurzeit gemacht werden könnten – vermutlich schaffen das die Radioastronomen in etwa fünf Jahren mittels Interferometrie.
Dennoch sind diese Rechnungen schon seit Jahren nützlich für die Astronomen: In einem weiteren numerischen Schritt kann man aus dem Bild ein Spektrum ausrechnen. Die sind sehr wohl beobachtbar! Da die Materie so nah an einem Schwarzen Loch sehr heiß ist, liegt hier ein Gemisch aus Ionen und Elektronen vor, ein Plasma. Es ist so heiß, dass es typischerweise im Röntgenbereich strahlt. Entsprechend wird relativistisches Ray Tracing genutzt, um Röntgenspektren zu simulieren, insbesondere Wärmestrahlung der Scheibe (engl. relativistic multi-color black body) und Eisenfluoreszenzlinien (Fe Kα). Auch der Vergleich mit Radiospektren ist möglich, wenn man annimmt, dass Synchrotronstrahlung in der Nähe des Loches von relativistischen Elektronen abgestrahlt wird.
Der Vergleich aus Simulation und Beobachtung erlaubt Rückschüsse auf Eigenschaften des inneren Akkretionsflusses und sogar auf das Schwarze Loch, z.B. ob es rotiert.

Mehr dazu im Wissensportal

• Web-Artikel: Gefangenes Licht – Relativistisches Ray Tracing
• Vortrag: Relativistic Emission Lines of Accreting Black Holes (Stand Mai 2003)
• Diplomarbeit von Andreas Müller (2000): Emissionslinienprofile relativistischer Scheiben um rotierende Schwarze Löcher, pdf (3.9 MB)
• Doktorarbeit von Andreas Müller (2004): Black Hole Astrophysics: Magnetohydrodynamics on the Kerr geometry, pdf (9.9 MB)
• Müller, A. & Camenzind, M.: Relativistic emission lines from accreting black holes – The effect of disk truncation on line profiles, , A&A 413, 861, 2004; Preprint: astro-ph/0309832