Als Gravitationslinsen bezeichnen Astrophysiker generell Objekte, die allein aufgrund ihrer hohen Masse, Strahlung signifikant abzulenken vermögen. Gemäß der Allgemeinen Relativitätstheorie (ART) kann das jede Masse, weil sie die Raumzeit lokal krümmt und damit die Bahnen anderer Teilchen und von Strahlung, die Geodäten, beeinflusst. In der Praxis wichtig ist der Effekt nur bei hohen, kompakten Massen, weil sie eine größere Ablenkung der Bahnen bewirken.

Massen als Linsen

Strahlung folgt gemäß der Allgemeinen Relativitätstheorie den Nullgeodäten einer Metrik. Im uns vertrauten Fall einer flachen Metrik, der Minkowski-Geometrie, bewegt sich das Licht auf Geraden. Dies ist der Grenzfall der geometrischen Optik. Im allgemeinen Fall jedoch ist die Metrik gekrümmt durch die Anwesenheit von Materie und Energie. Die Nullgeodäten sind dann ebenfalls gekrümmt und können über das Lösen der Geodätengleichung ermittelt werden.
In Analogie zu einer Linse, die parallel zur optischen Achse einfallende Lichtstrahlen in ihrem Brennpunkt vereint, lenkt Masse über die Raumkrümmung Strahlung ab.

Linsen der Kosmologie

Bedeutsame Gravitationslinsen in der Astronomie sind massereiche Galaxienhaufen (engl. galaxy cluster) oder Ansammlungen von Dunkler Materie. Die Dunkle Materie ist anteilig neben der 'normalen' baryonischen Materie in jeder Galaxie enthalten und beherrscht deren Dynamik und Entwicklung. In Galaxienhaufen macht der Massenanteil an Dunkler Materie sogar 90% aus, nur 1% ist sichtbar in Form von Sternen, der Rest ist intergalaktisches Gas! Der gesamte Materieinhalt bestimmt die Dynamik des Haufens und führt zu heftigen Gezeitenwechselwirkungen zwischen den einzelnen Clustergalaxien. Dies kann zu kannibalistischen Szenarien führen, wo Galaxien miteinander verschmelzen (engl. merging) oder sich große Galaxien kleinere einverleiben. Dies resultiert häufig in irregulären Galaxien (siehe Hubble-Klassifikation), wie den prominenten Antennengalaxien (siehe Bild und Beschreibung unter dem Eintrag Gezeitenkräfte). Ein anderes schönes Beispiel eines 'Unfalls der Materiegiganten' zeigt die Abbildung rechts. Dieses Foto des Weltraumteleskops Hubble zeigt rechts NGC 2207 und links IC 2163 im Sternbild Großer Hund (Canis Major). Die Spiralgalaxien kommen sich etwas zu nahe. Somit treten sie in Interaktion durch Gezeitenkräfte: Sterne werden hinausgeschleudert, das interstellare Gas beider Spiralen vermischt sich und regt die Sternentstehung an, eventuell verschmelzen auch früher oder später die Kerne der Galaxien – sprich die supermassereichen Schwarzen Löcher – weil ihr 'Tanz' durch die Abstrahlung von Gravitationswellen immer enger wird. Aus der Durchmischung der Welten entstehen neue Welten und vielleicht sogar neues Leben (Credit: Merritt et al. 2004, NASA/ESA).

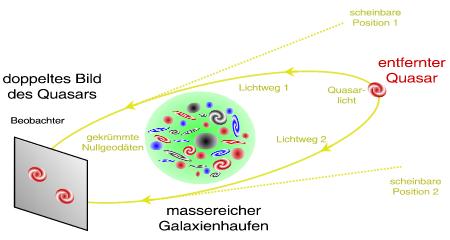
kosmischer Schwips: Doppel- und Mehrfachbilder

Wenn Galaxienhaufen als Gravitationslinsen wirken, fokussieren sie die Strahlung derjenigen kosmischen Objekte, die hinter ihnen und nahe entlang der Sichtlinie liegen. Dabei können auch Mehrfachbilder ein und desselben Objekts auftreten, weil die Strahlung auf verschiedenen Lichtwegen zum Beobachter gelangt. Es handelt sich gewissermaßen um eine 'kosmische optische Täuschung' (siehe Abbildung oben). Häufig beobachten Astronomen bei Galaxienhaufen verzerrte Bilder einzelner Galaxien, die dann als fadenförmige Gebilde auf Aufnahmen in Erscheinung treten (siehe Objekte im Abell-Katalog). Manchmal entsteht auch ein charakteristisches rundes Gebilde, der so genannte Einstein-Ring. Hier sind die Verhältnisse zwischen Linse und gelinstem Objekt besonders symmetrisch.

klein, aber Linse

Außerdem gibt es kleine Ansammlungen von Materie, die als Mikrolinsen fungieren. Ihre Masse ist so gering, dass man kein aufgelöstes verzerrtes Abbild, aber einen charakteristischen, symmetrischen Helligkeitsanstieg eines Sterns oder eines anderen strahlenden Objekts erhält, wenn eine solche Mikrolinse genau zwischen Beobachter und gelinstem Objekt vorüberzieht. Auch das wurde bereits beobachtet und hat eine Relevanz bei den MACHOs, den Massive Compact Halo Objects. Diese leuchtschwachen Objekte befinden sich im Halo der Milchstraße und können so indirekt über Mikrolinsen-Ereignisse (engl. microlensing events) in Anzahl und Masse abgeschätzt werden. Vermutlich handelt es sich bei den MACHOs um Braune Zwerge oder M-Zwerge (massearme Sterne vom SpektraltypM), die sich im Halo der Milchstraße bewegen (z.B. Gaudi & Han 2004, astro-ph/0402417).
Die Mikrolinse kann allerdings auch ein Stern sein, der mindestens einen Planet hat. So eignet sich der Gravitationslinseneffekt zur Suche und Identifikation von Planeten. Der erste Kandidat für dieses Planetarische Mikrolinsen-Ereignis (engl. planetary microlensing event) ist das Objekt OGLE 2003-BLG-235/MOA 2003-BLG-53 (katalogisiert nach den MOA und OGLE Beobachtungen). Diese Linse hat eine Entfernung von 5.2 kpc und ist Sternen im Galaktischen Zentrum in etwa 8 kpc Distanz vorgelagert. Zufällig liegen Hintergrundstern und Mikrolinse ziemlich exakt auf einer Linie. So erscheint das Licht des Hintergrundsterns für kurze Zeit in der Form eines winzigen Einstein-Rings an der Himmelssphäre. Astronomen beobachteten für die Dauer von etwa einer Woche eine schwache Abweichung (Spikes) in der Lichtkurve des Hintergrundsterns. Herkömmliche Modelle für das davor liegende Linsensystem mit einzelnen, linsenden Objekten versagen, um diese besondere Lichtkurve anzupassen. Spikes sind ein Charakteristikum von Linsen, die aus einem Binärsystem bestehen. Es stellte sich heraus, dass die Massen der beiden Linsenkomponenten sehr verschiedenen voneinander sind. Die Astronomen um Ian Bond schlagen deshalb ein Linsensystem aus Stern mit Planeten vor, um den Anstieg der Lichtkurve zu erklären. Setzt man für den Stern an, dass es sich um einen Hauptreihenstern (speziell ein M-Zwerg mit 0.4 Sonnenmassen) handelt, so hätte der Planet etwa 1.5 Jupitermassen und umkreiste den Stern in einem Abstand von etwa drei Astronomischen Einheiten (Abkürzung AU). Die exotischere Alternative für das Binärsystem wäre ein Weißer Zwerg mit nur 0.6 Sonnenmassen, der dann in 2.8 AU einen Planet mit 2.5 Jupitermassen umkreiste (Bond et al. 2004, astro-ph/0404309).

Die Mutter aller Gravitationslinsen

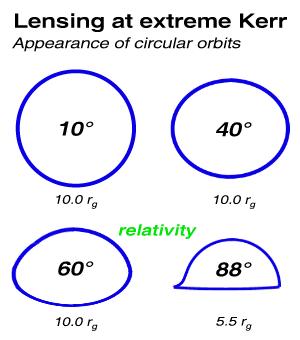Neben den Galaxienhaufen und Mikrolinsen sind die Schwarzen Löcher ein weiterer Kandidat für Gravitationslinsen. Auch hier kann man die verzerrten Bilder nicht direkt aufgelöst beobachten, sondern muss die Verzerrung spektroskopisch ableiten. Das numerische Verfahren Ray Tracing bietet eine Möglichkeit im Computerlabor die gelinsten, verzerrten Objekte zu studieren. So kann man die scheinbare Deformation von Akkretionsscheiben beobachten, wenn man sie unter hohen Neigungen beobachten würde. Gleiches gilt für enge Umlaufbahnen um Schwarze Löcher. Die Abbildung links zeigt simulierte Kreisbahnen um ein Schwarzes Loch, die einen Abstand von 5 bis 10 Gravitationsradien zum zentralen, maximal rotierenden Schwarzen Loch (nicht dargestellt) haben (A. Müller, Dissertation 2004). Es handelt sich bei allen vier Fällen um Primärbilder, also nur um Strahlung, die direkt zum Beobachter propagiert. Wichtig ist nun, dass man die klassische elliptische Bahnform nur bei kleinen Neigungen (Inklinationen) der Bahnebene hat, wie die beiden oberen Darstellungen belegen. Bei höheren Inklinationen hingegen, etwa ab 60 Grad, machen sich deutlich die relativistischen Linseneffekte bemerkbar: Der Beobachter blickt zwar eher auf die Kante der Bahnebene, aber die Strahlung wird um die kompakte Masse herumgelenkt. So kann man auch Bereiche direkt hinter dem Loch beobachten, die sich im geometrischen Schatten befinden und Newtonsch unbeobachtbar wären. Bei der hier höchsten Inklination von 88 Grad, was sehr nahe am Maximum von 90 Grad liegt, erhält man ein stark verzerrtes Abbild des Orbits: Obwohl der Beobachter fast exakt auf die Kante der Bahnebene schaut, wo die klassische Ellipse wie eine Linie erscheinen und der Orbiter auf ihr hin- und her oszillieren würde, sieht man in diesem gelinsten Beispiel den hinteren Teil des Bahnorbits! Leider reichen die aktuellen Auflösungen der Teleskope nicht aus, um solch befremdliche Bahnbewegungen am Himmel zu beobachten. Wenn dies gelänge könnte man den Umlaufsinn der Lochrotation direkt sehen! Denn die Links-Rechts-Asymmetrie ist auf den Frame-Dragging-Effekt zurückzuführen: Das rotierende Loch zieht den Orbiter mit sich mit. Im hier gerechneten Beispiel rotiert das Loch maximal (Kerr-Parameter a = M in geometrisierten Einheiten) im Gegenuhrzeigersinn. Deshalb befindet sich bei der Bahnform unter 88 Grad die kleine Ausstülpung der beobachteten Bahn links unten. Auf der gleichen Seite zeigen leuchtende Standardakkretionsscheiben das charakteristische Vorwärts-Beaming, ein Gebiet hoher Blauverschiebung.
Neben der starken Abhängigkeit von der Inklination, spielt natürlich der Abstand des Orbits zum Loch eine gewichtige Rolle. Bei großen Abständen verschwinden die relativistischen Linseneffekte, weil man in den asymptotisch flachen Bereich der Raumzeit Schwarzer Löcher kommt. Dieser Fall ist aktuell bei demjenigen Stern mit der Bezeichnung S2 beobachtbar, der als Stern mit engster Bahn das supermassereiche Schwarze Loch im Galaktischen Zentrum (etwa 3 Millionen Sonnenmassen) umkreist. S2 ist zwar mit einer Periastronentfernung von 17 Lichtstunden sehr nahe am Loch, doch entspricht diese Entfernung im relativistischen Einheitensystem gewaltigen 4142 Gravitationsradien. Diese Distanz ist zu groß (vergleiche 5 bis 10 Gravitationsradien in Abbildung), als dass relativistische Effekte, wie Linsenbeugung eine Rolle spielen würden: die Bahnform von S2 ist eine exakte Kepler-Ellipse (siehe Kepler-Gesetze).
Die Verhältnisse sind bei linsenden Schwarzen Löchern tatsächlich noch komplizierter: Neben den dargestellten Primärbildern entstehen Bilder höherer Ordnung dadurch, dass eng am Loch vorbeilaufende Strahlung das Loch mehrfach umrunden kann (unter gewissen Umständen kann es sogar auf dem Photonenorbit eingefangen werden). So gibt es im Allgemeinen noch Sekundär- und Tertiärbilder, die es bei flachen Standardakkretionsscheiben ermöglichen, die Newtonsch unbeobachtbare Unterseite der Scheibe zu beobachten!
Was rechtfertigt den Titel dieses Eintrags 'Mutter aller Gravitationslinsen'? Nun, Schwarze Löcher sind die extremste Form einer Gravitationslinse, weil die Linse sogar das Licht ab einer kritischen Grenze namens Ereignishorizont einzufangen vermag. Aus diesem Grund sind Schwarze Löcher schwarz.

Werkzeuge der modernen, experimentellen Kosmologie

Gravitationslinsen erweisen sich als äußerst nützlich für die Kosmologie: leuchtschwache Objekte werden durch den Einfluss einer Linse verstärkt, so dass ein größerer Strahlungsfluss gemessen werden kann, als ohne Linse. Dies ermöglicht es den Astronomen noch tiefer in den Kosmos zu schauen. Der aktuelle Entfernungsrekordhalter Abell 1835 IR 1916 ist eine Galaxie mit einer Rotverschiebung von z = 10! Astronomen aus der Schweiz, Frankreich und Kalifornien beobachteten mit der Infrarot-Kamera ISAAC (Infrared Spectrometer And Array Camera) des Very Large Telescope (VLT) in Chile diese schwache Infrarotquelle im Galaxienhaufen Abell 1835. Ihre Strahlung wird durch eine Gravitationslinse im Vordergrund um einen Faktor 25 bis 100 verstärkt. Die Gesamtmasse dieser sehr jungen Galaxie wurde zu nur 500 Mio. Sonnenmassen (inklusive Dunkle Materie im Halo) abgeschätzt (Pello et al. 2004, astro-ph/0403025).
Diese Entdeckung übertrumpfte den nur zwei Wochen vorher aufgestellten Rekord einer Galaxie bei z ~ 7 (Kneib et al. 2004). Auch hier fokussiert der vorgelagerte Galaxienhaufen Abell 2218 die auf der Erde als Infrarotstrahlung detektierte Strahlung und verstärkt sie um einen Faktor 25. Ohne den linsenden Galaxienhaufen hätte man dieses Objekt, das bereits 750 Millionen Jahre nach dem Urknall sein Licht aussandte, nicht entdeckt.

Einstein, der Visonär

Albert Einstein spekulierte schon 1936 auf der Basis seiner Theorie über die Existenz von Gravitationslinsen. Er selbst hatte es nicht für möglich gehalten, dass man dies je beobachten würde (siehe Einstein-Ring für Einzelheiten). Heute ist eine Vielzahl von gelinsten Objekten bekannt (Abell-Katalog). Viele Quasare sind darunter, die Doppelbilder, Einsteinkreuze und Einstein-Ringe zeigen. Ein prominentes Beispiel ist das scheinbare Quasarpaar Q2345+007 in einer Entfernung von z = 2.15 (siehe Rotverschiebung). Eine Linse konnte für dieses Doppelbild nicht beobachtet werden. Aus diesem Grund vermutet man eine Ansammlung von Dunkler Materie als Gravitationslinse (Green et al. 2002, astro-ph/0202081).
Einen ähnlichen Effekt wie bei den Gravitationslinsen erwartet man beim 'topologischen Linsen'. Diese 'Geisterbilder' sind dann auf eine komplexe Topologie des Universums zurückzuführen. Bisher hat man das noch nicht bewusst beobachtet. Die Erscheinung wäre derjenigen, die von Gravitationslinsen resultiert vergleichbar, kann aber auch bis zur Unkenntlichkeit, bis zur perfekten optischen Täuschung, verzerrt sein. Vielleicht spielt uns der Kosmos so manchen Streich – und wir merken es nicht einmal.

Linsen verzerren den Hintergrund

Der Gravitationslinseneffekt ist auch deshalb bedeutsam in der Kosmologie, weil die überall verteilte Materie in Form von Galaxien, Galaxienhaufen und intergalaktischer Materie die kosmische Hintergrundstrahlung beeinflusst. Dieser Vorgang muss berücksichtigt werden, wenn die Kosmologen aus der Hintergrundstrahlung Eigenschaften des Universums herauslesen möchten. Es konnte gezeigt werden, dass enge Strukturen im CMB-Spektrum ausgeschmiert und geglättet werden (Zaldarriaga & Seljak, PRD 1998). Der Effekt kann bis zu 10% betragen.