Die Minkowski-Metrik beschreibt den flachen Raum, also eine vierdimensionale Mannigfaltigkeit ohne Krümmungen, d.h. in Abwesenheit von Massen oder Energien. In Berechnungen wird diese Metrik auch benutzt, wenn lokale Krümmungen vernachlässigbar sind, weil die Energien betrachteter Testteilchen (Photonen etc.) sehr klein sind.

Metrik der SRT

Die Minkowski-Metrik ist die Metrik oder Raumzeit der Speziellen Relativitätstheorie (SRT). Sie wurde nach dem Mathematiker Hermann Minkowski (1864 – 1909) benannt, der die elegante Formulierung der Zusammenfassung von Raum und Zeit 1908 begründet hat. Minkowski war der Mathematikprofessor von Albert Einstein und fand nach der Veröffentlichung der SRT (1905) die bündige Schreibweise in Vierervektoren und Matrizen.

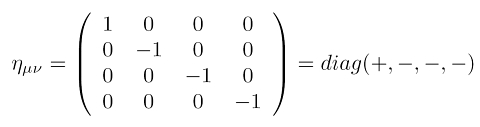
einfache Eigenschaften

Die Metrik hat eine sehr einfache, mathematische Gestalt: Oben ist der metrische Tensor der Minkowski-Metrik als 4 × 4-Matrix dargestellt. Wie man unmittelbar sieht, ist die Matrix diagonal. Auf der Hauptdiagonalen der Matrix stehen die Zahlen 1, -1, -1, -1; in der Relativitätstheorie hat man die Freiheit auch die Folge -1, 1, 1, 1 zu wählen. Die Signatur, also der Überschuss an positivem oder negativem Vorzeichen bei der Summenbildung der Diagonalelemente, ist entsprechend -2 oder +2. Im Unterschied zur Allgemeinen Relativitätstheorie (ART) sind die Matrixkomponenten konstant und hängen nicht von den Raum- oder der Zeitkoordinate ab. Die Minkowski-Metrik ist eben im Unterschied zu den Raumzeiten der ART flach und überall in der Raumzeit gleich. Dass die Matrixkomponenten vom Betrag her 1 sind, liegt daran, weil relativistische Einheiten mit der Vereinfachung Vakuumlichtgeschwindigkeit c = 1 gewählt wurde (siehe auch geometrisierte Einheiten).
Damit ähnelt die Minkowski-Metrik zwar der Euklidischen Metrik – der Unterschied besteht nur in einem Vorzeichen, der jedoch gewichtig ist und die Lichtkegelstruktur von Raum und Zeit in der SRT prägt.
Die Minkowski-Metrik ist ein Zustand sehr hoher Symmetrie: sie besitzt zehn Killing-Vektoren.