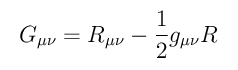Der Einstein-Tensor ist einer der wesentlichen Tensoren in der Allgemeinen Relativitätstheorie (ART). Er ist gerade die linke Seite der Einsteinschen Feldgleichungen, während die rechte Seite im Vakuumfall verschwindet, im allgemeinen Fall jedoch gleich dem Energie-Impuls-Tensor plus Lambda-Term (siehe kosmologische Konstante) ist.

Wir basteln uns einen Einstein-Tensor

Der Einstein-Tensor setzt sich tensoriell aus dem Ricci-Tensor (2. Stufe) und dessen Verjüngung, dem Ricci-Skalar (Tensor 0. Stufe), zusammen. Der Ricci-Tensor selbst ist ebenfalls eine Verjüngung des Riemann-Tensors (4.Stufe). Das rechtfertigt auch die Bezeichnung Einsteinscher Krümmungstensor. Der Riemann-Tensor besteht wiederum aus partiellen Ableitungen der Christoffel-Symbole, die selbst Ableitungen der Metrik sind. Das klingt kompliziert, daher noch einmal die Vorgehensweise bei bekannter Metrik (= Raumzeit):

• die Ableitungen des metrischen Tensors liefern die Christoffel-Symbole;
• die Ableitung der Christoffel-Symbole bilden den Riemann-Tensor 4. Stufe;
• die Verjüngung des Riemann-Tensors und die weitere Verjüngung des daraus folgenden Ricci-Tensors zum Ricci-Skalar konstituieren zusammen mit dem metrischen Tensor den Einstein-Tensor.

Im Einstein-Tensor steckt verbogener Raum (und verbogene Zeit)

Der Einstein-Tensor enthält also die ganze Information über die Raumzeit und wird durch kompliziertes Verschachteln der metrischen Koeffizienten erzeugt.