Das Higgs-Teilchen oder Higgs-Feld wurde nach dem britischen Physiker Peter W. Higgs benannt, der dessen Existenz bereits 1964 prognostizierte. Es handelt sich um ein elektrisch neutrales Austauschboson mit Spin 0 (also einem Skalarfeld), dessen Masse sehr hoch sein muss. Experimentell ließ sich die Massengrenze oberhalb von 114 GeV (LEP-Experiment am CERN) einordnen. Zum Vergleich: die Nukleonen im Atomkern, Proton und Neutron, haben eine Masse von etwa 1 GeV.

Der Higgs-Mechanismus

Das hypothetische Higgs-Teilchen hat eine wichtige Funktion im Teilchenzoo der Physik: Im Higgs-Mechanismus stattet das Higgs-Feld, das sich unendlich im Raum erstreckt, die Teilchen mit Masse aus. Es handelt sich um eine spontane Symmetriebrechung, die wie folgt abläuft: Das Higgs-Boson koppelt an sämtliche Teilchen, d.h. es kann mit jedem Teilchen wechselwirken. Dabei ist die Stärke dieser Kopplung proportional zur Masse des Teilchens. Dadurch dass das Higgs-Boson nun an alle Teilchen koppelt, verschafft es ihnen Schwere: die Teilchen erhalten eine Masse.

Symmetrie bricht, Teilchenmasse da

Die meisten Teilchen, die Physiker beobachten, haben eine Masse. Der Higgs-Mechanismus hat also offensichtlich schon stattgefunden. Genauer: Die Symmetriebrechung muss bei einer höheren Temperatur, als diejenige die für unsere Umgebung typisch ist, stattgefunden haben. Im Higgs-Modell nimmt man nun an, dass die Symmetrie bei einer kritischen Temperatur gebrochen wurde und in eine Aufspaltung in die bekannten vier Naturkräfte ('Tetralogie der Kräfte') gemündet habe.

Die vier fundamentalen Wechselwirkungen heißen

• Gravitation,
• elektromagnetische Wechselwirkung,
• Schwache Wechselwirkung
• und Starke Wechselwirkung.

Aber das war nicht immer so...

Oberhalb der kritischen Temperatur wird die Symmetrie restauriert und es gibt nur zwei Naturkräfte: X-Kraft und Gravitation. Die Großen Vereinheitlichten Theorien (GUT) beschreiben, wie die Symmetrie zwischen elektromagnetischer, schwacher und starker Kraft im Rahmen einer SU(5)-Gruppentheorie hergestellt werden kann. Die GUT-Skala ist sehr nahe an der fundamentalen Planck-Skala: typische Energien liegen im Bereich von 10¹⁶ GeV, was gemäß E = kT (k: Boltzmann-Konstante) Temperaturen von 10²⁹ Kelvin entspricht. Das ist ein recht unangenehmes Milieu für Leben und sie war – so die gängige Auffassung in der modernen Kosmologie – im sehr frühen Universum realisiert (GUT-Ära).

Festkörper wiesen den Weg

Das Konzept, das heute Higgs-Mechanismus genannt wird, wurde von Higgs aus der Festkörperphysik übernommen. Im Festkörper gibt es ein Gitter aus positiv geladenen Atomrümpfen, die das Gitter des Festkörpers bilden. Bewegt sich nun ein Elektron durch das Gitter, so wird dessen effektive Masse signifikant gegenüber der eines freien Elektrons erhöht, weil das Elektron vom positiven Gitter angezogen wird. Das Elektron wird schwerer!
Auf analoge Weise soll das Higgs-Teilchen den schweren W⁺-, W^-- und dem Z-Teilchen, den Weakonen der schwachen Wechselwirkung, ihre Masse verleihen, nur nicht dem (ruhe-)masselosen Photon. Die hohen Massen der intermediären Eichbosonen W⁺, W^- und Z motivieren stark die Existenz des Higgs-Bosons in der Teilchenphysik.

gespenstisches Higgs-Teilchen

Gemäß der quantenmechanischen Energie-Zeit-Unschärfe nach Werner Heisenberg ist mit einer hohen Masse eines Teilchens eine kurze Lebensdauer assoziiert, und gerade das macht den Nachweis des Higgs-Teilchens so schwierig. Aus diesem Grund könnte man das Higgs-Teilchen auch Geistteilchen (engl. ghost) nennen, weil es kaum in Erscheinung tritt. Historisch geht die Bezeichnung 'Geistteilchen' auf Abdus Salam zurück, der eine anschauliche Interpretation des Higgs-Mechanismus beschrieb (sinngemäß): 'Teilchen verleiben sich Higgs-Bosonen ein, um an Masse zu gewinnen und zurück bleiben nur die Geister der Higgs-Teilchen.' Eine andere Bezeichnung ist das 'Teilchen Gottes', weil ihm die tragende Rolle bei der Vergabe der Masse zukommt.

Noch keine experimentelle Bestätigung!

Es ist das letzte Teilchen im Standardmodell der Teilchenphysik, dessen experimenteller Nachweis fehlt! Die Ergebnisse des Fermilab sowie des CERN, wenn der neue Teilchenbeschleuniger LHC im Ende 2007 steht, bleiben mit Spannung abzuwarten. Nur sie dringen in den interessanten Energiebereich des Higgs-Teilchens vor.

SUSY macht mehr Higgs-Teilchen

Die Supersymmetrie (SUSY) stellt eine Erweiterung des Standardmodells dar. Sie prognostiziert weitere Teilchen, so genannte Superpartner, zu den beobachteten Teilchen. Diese Erweiterung betrifft auch das Higgs-Teilchen. Unter Berücksichtigung der Supersymmetrie gibt es nicht nur ein Higgs-Teilchen, sondern fünf Higgs-Teilchen: drei elektrisch neutrale und zwei elektrisch geladenen Higgs-Teilchen. Das Minimale Supersymmetrische Standardmodell (MSSM) sagt sogar eine Maximalmasse der Higgs-Teilchen voraus, die bei etwa 130 GeV liegt. Zusammen mit der experimentell am CERN verifizierten Minimalmasse von 114 GeV bleibt dem Higgs-Feld nur ein schmaler Massenbereich, den die Physiker an der Generation kommender Teilchenbeschleuniger genau sondieren werden. Möglicherweise steht Verifikation oder Falsifikation kurz bevor!

Verallgemeinerung zu Nambu-Goldstone-Bosonen

Der Higgs-Mechanismus ist immer mit einer spontanen Symmetriebrechung (SSB) verbunden. Bei diesen Brechungen der Symmetrie treten aber auch immer so genannte topologische Defekte (domain walls, kosmische Strings, magnetische Monopole etc.) auf. Der Higgs-Apparat ist jedoch weit verbreiteter in der Natur, als nur in der Festkörperphysik und Teilchenphysik. Dieses fundamentale Konzept wurde bereits in vielen anderen Disziplinen angewendet. So kann man in der Kosmologie (Phasenübergang im frühen Universum) und Quantenchromodynamik (Peccei-Quinn-Symmetrie) Symmetriebrechungen finden, die immer mit einem skalaren Higgs-Feld beschrieben werden können. Man nennt diese mit dem Feld assoziierten Teilchen dann allgemeiner Nambu-Goldstone-Bosonen. Das Higgs-Teilchen ist demnach nur eine spezielle Realisierung eines Nambu-Goldstone-Bosons.

Symmetriebrechung anschaulich

Die Theoretiker betrachten in der Regel ein skalares Higgs-Feld, das mit dem Higgs-Potential assoziiert ist. Das Skalarfeld im Raum- und Zeitpunkt nimmt eine bestimmte Feldenergie an, die gerade diesem Higgs-Potential entspricht. Skalarfelder sind lorentzinvariant, d.h. sie haben die angenehme Eigenschaft sich unter Lorentz-Transformationen nicht zu verändern: Jeder Beobachter misst den gleichen Wert für dieses Feld, unabhängig davon, wo er sich befindet oder wie schnell er sich bewegt. Der Wertebereich dieses Feldes kann wiederum reell, komplex, vektor- oder matrixwertig sein. Das Entscheidende ist, dass sich die Vakuumzustände des Feldes am Boden der Potentialmulde befinden – analog zu stabilen Gleichgewichtslagen in der klassischen Mechanik.

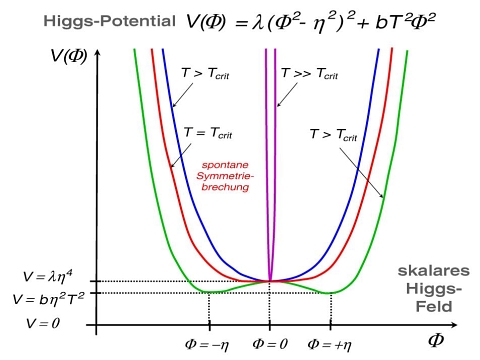
Die Abbildung oben (große Version) illustriert den Potentialverlauf für ein reelles Higgs-Potential, parametrisiert durch die Temperatur. Die Vakuumzustände hängen von einer kritischen Temperatur ab, bei der gerade die Symmetriebrechung stattfindet (rote Kurve). Oberhalb dieser Temperatur existiert eine höhere Symmetrie: es existiert nur ein globales Minimum, nämlich dort, wo das Feld verschwindet (blaue und violette Kurven). Unterhalb der kritischen Temperatur hingegen ist diese Symmetrie gebrochen: das globale Minimum wird zum lokalen Maximum und sowohl links als auch rechts davon treten zwei neue globale Minima auf (grüne Kurve). Eine Kurvendiskussion (Analysis einer Veränderlichen) liefert die parametrisierten Koordinaten 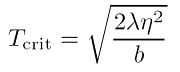der Extrema und Wendepunkte und die Gleichung für die kritische Temperatur (siehe Gleichung links). An der Abbildung sieht man auch, dass der Vakuumerwartungswert des Higgs-Feldes (Moduli), der gerade mit der Potentialmulde assoziiert ist, nach der Symmetrieberechung absinkt. Denn das Feld wird jede Fluktuation ausnutzen, um von dem Potentialberg (instabile Gleichgewichtslage) 'abzurutschen' und in eines der beiden Minima zu gleiten, die stabile Zustände sind. Das ist eine wunderbare Analogie zu Gleichgewichtslagen in der klassischen Mechanik!

Und wer's komplex mag...

Die komplexe Erweiterung dieses Potentials kann einfach durch Rotation der Funktion um die y-Achse (Ordinate) generiert werden. Die entsprechende Potentialfläche hat die Gestalt eines mexikanischen Sombrero-Hutes, weshalb auch die englische Bezeichnung Mexican hat potential für das komplexe Higgs-Potential gebräuchlich ist. Die beiden Vakuumzustände unterhalb der kritischen Temperatur degenerieren dann. Man sagt: die Vakuum-Mannigfaltigkeit (Moduli-Raum, engl. Moduli space) ist ein Kreis. In einem dreidimensionalen Koordinatensystem wird die Basisfläche durch den Real- und Imaginärteil des Feldes aufgespannt. Die Vakuumzustände auf dem Kreis können durch einen Phasenwinkel parametrisiert werden. Die Rotationssymmetrie für komplexwertige Higgs-Felder nennt man U(1)-Symmetrie, gemäß der Gruppentheorie.

Anknüpfung an die Kosmologie

Diese mathematischen Eigenschaften des reellen Higgs-Potentials interpretiert man kosmologisch folgendermaßen: Kurz nach dem Urknall herrschten sehr hohe Temperaturen oberhalb der GUT-Skala von 10²⁹ K. Das Higgs-Feld nahm im gesamten Raum den Wert null an, weil die Symmetrie noch nicht gebrochen war (entsprechend einem globalen Minimum). Durch die Expansion des heißen Feuerballs kühlte dieser langsam ab, die Temperatur sank und näherte sich der kritischen GUT-Temperatur. Dann setzte der Phasenübergang ein: die Symmetrie wurde spontan gebrochen. Das reelle Higgs-Feld hat nun zwei mögliche Vakuumerwartungswerte, das komplexe sogar mehr, die sich durch einen Phasenwinkel unterscheiden. Das 'Spontane' an der Symmetriebrechung ist, dass a priori nicht klar ist, welchen der beiden Vakuumwerte das reelle Higgs-Feld annehmen wird. Dies unterliegt einer statistischen Verteilung. Das 'Springen' des Vakuumerwartungswertes des Higgs-Feldes von null auf einen endlichen Wert treibt gerade die Inflation an, eine exponentielle Expansion des Universums. Weil diese Ausdehnung schneller als das Licht sein kann, können voneinander kausal entkoppelte Gebiete entstehen, die verschiedene Erwartungswerte für das Vakuum haben.

Der falsche Hase des Nichts

Das Problem ist nun, dass das Higgs-Feld eine stetig differenzierbare Funktion ist, also keine Unstetigkeiten in Form von 'Sprüngen' aufweisen darf. Zwischen zwei verschiedenen Erwartungswerten muss es demzufolge Gebiete geben, die verschwindendes Higgs-Feld haben, aber (im Gegensatz zum globalen Minimum oberhalb der kritischen Temperatur) endliches Higgs-Potential. Diese Gebiete heißen falsches Vakuum. Der endliche Erwartungswert für das Vakuum impliziert lokal eine endliche Energie, die eingeschlossen ist. Physiker nennen sie auch domain walls, die ein Beispiel für topologische Defekte darstellen. In drei Dimensionen trennen sie unterschiedliche Vakua voneinander. Ihr Feldverlauf entspricht mathematisch dem Tangens Hyperbolikus, der in der nächsten Abbildung illustriert ist:

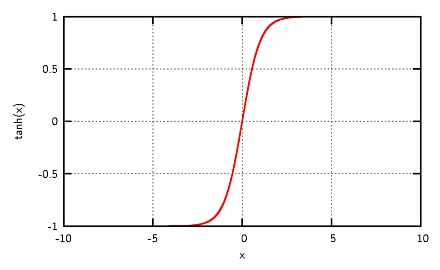
Die beiden unterschiedlichen Niveaus links und rechts entsprechen den unterschiedlichen Vakua zwischen denen die domain walls vermitteln. Leider beobachteten die Astronomen diese domain walls bislang nicht.

Werden Gravitationswellen helfen?

Im Zuge dessen führte man das komplexe Higgs-Feld ein (das man sich aus zwei reellen Higgs-Felder zusammengesetzt denken kann, Real- und Imaginärteil). In dieser Erweiterung treten ebenfalls topologische Defekte auf: die kosmischen Strings (die nicht mit den Strings der Stringtheorien zu verwechseln sind!). Sie weisen eine andere Topologie als domain walls auf und bestehen ebenfalls aus Einschlüssen des falschen Higgs-Vakuums. Mathematisch gesprochen handelt es bei den kosmischen Strings um eindimensionale Vertex-Linien. In dessen Kernen verschwindet zwar das Higgs-Feld, aber da die Gebilde ausgedehnt sind (entweder geschlossen oder unendlich lange) kann man sich vorstellen, dass sie einen nicht unerheblichen Teil an Feldenergie gespeichert haben. Weil die Theoretiker außerdem annehmen, dass die Strings oszillieren, müssen sie auch Gravitationswellen aussenden. Das macht dieses Szenario wieder interessant für die Astronomen, nämlich für die in den letzten Jahren mächtig vorangetriebenen Gravitationswellendetektoren.

andere kosmische Saiten aufziehen

1976 wurde erstmals von T.W.B. Kibble in Erwägung gezogen, dass kosmische Strings eine Bedeutung für die Entwicklung des Universums haben könnten. Kosmische Strings bilden ein Netzwerk aus und wechselwirken miteinander durch Interkommutation. Damit bezeichnet man einen Austausch von Stringstücken, wenn sich kosmische Strings nahe genug kommen. Diese Wechselwirkung und auch die Expansion der Raumzeit, auf dessen Hintergrund die Strings 'mitschwimmen', führen zu einem allmählichen Aufzehren der im String gespeicherten Feldenergie. Dieser Zerfall führt – so vermuten Kosmologen – letztendlich zu einem Verschwinden kosmischer Strings, so dass in unserem lokalen Universum nur wenige – wenn überhaupt – vorhanden sein dürften. Der Durchmesser der kosmischen Strings liegt nur drei Größenordnungen über der Planck-Länge, bei etwa 10^-30 cm. Die Energie, die ein Kilometer String enthält, ist enorm und beträgt etwa 10⁵⁰ GeV.
Sollte es sie im frühen Universum gegeben haben, könnten sie für die Strukturbildung entscheidend gewesen sein. Sowohl Beobachtung als auch numerische Simulation zeigen filament- und wabenartige Strukturen, die aus Galaxien und Galaxienhaufen bestehen. Vielleicht waren die die Netzwerke kosmischer Strings als Relikte einer Symmetriebrechung die Kondensationskeime für die Galaxien? Man kann auch darüber spekulieren, dass an kosmischen Strings superkritische Brill-Wellen emittiert wurden, die zur Bildung der ersten Generation Schwarzer Löcher führten, die danach durch Akkretion wuchsen und zu den heute paradigmatisierten supermassereichen Schwarzen Löchern wurden. Aber das ist eine sehr gewagte und unkonventionelle Hypothese.

Literaturquellen:

• A. Rajantie, Defect formation in the Early Universe, astro-ph/0307387 (2003),
• Franz Embacher, Kosmische Strings (1994)