Lexikon der Biologie: Gefangenendilemma
Gefangenendilemma, prisoners dilemma, ein mathematisches Konfliktmodell der Spieltheorie, das Interaktionen zwischen Individuen (Spielern) untersucht – unter der Annahme, daß das Verhalten aller Beteiligten von dem egoistischen Interesse jedes einzelnen bestimmt wird. Dabei wird untersucht, unter welchen Bedingungen dennoch kooperatives Verhalten (Kooperation) zustande kommen kann. Das Modell beschreibt folgende Situation: 2 Komplizen sind einer leichten Straftat überführt, für die sie 1 Jahr Gefängnis bekommen. Außerdem werden sie eines schweren Verbrechens verdächtigt, auf das zusätzlich 9 Jahre steht. Insgesamt drohen also 10 Jahre Gefängnis. Die Gefangenen werden getrennt verhört und erhalten ein Angebot: Gesteht einer das gemeinsam verübte schwere Verbrechen, wird er als Kronzeuge freigelassen (0 Jahre Gefängnis), und sein Komplize bekommt 10 Jahre Gefängnis. Gesteht der Komplize auch, wird beiden nur 1 Jahr erlassen (9 Jahre Gefängnis). Wenn beide leugnen, kann ihnen das schwere Verbrechen nicht angelastet werden (1 Jahr Gefängnis für die leichte Straftat). Für die beiden Spieler dieses Konfliktmodells gibt es nur 2 Möglichkeiten: gestehen oder leugnen. Der maximale Straferlaß tritt bei Gestehen ein, aber nur dann – und dies ist entscheidend –, wenn der Komplize leugnet. Welche Möglichkeiten sich ergeben, zeigt die Matrix in der Abb. (1 für die beschriebene Situation, 2 in verallgemeinerter Form; vgl. Abb. ). Spieler A muß, falls der andere leugnet, 1 Jahr ins Gefängnis, wenn er ebenfalls leugnet, und überhaupt nicht ins Gefängnis, wenn er gesteht. Falls der andere gesteht, kommt er 10 Jahre ins Gefängnis, wenn er leugnet, und 9 Jahre ins Gefängnis, wenn er ebenfalls gesteht. Da sich die Komplizen nicht absprechen können und sich nicht darauf verlassen können, daß der andere kooperiert, indem er auch leugnet, werden beide gestehen und folglich 9 Jahre absitzen müssen. Die Matrix in Abb. 2 ( vgl. Abb. ) zeigt in verallgemeinerter Form die Bedingungen des Spiels. Wenn, wie im Beispiel T > R > P > S ist, dann ist die Taktik, die auf „Ausbeuten“ des Partners angelegt ist („Gestehen“), evolutionsstabil. – Wenn die Partner jedoch wiederholt in die gleiche Situation geraten, dabei Erfahrungen sammeln können und ihr Verhalten davon abhängig machen, wie der vorhergehende Konflikt ausgegangen ist, dann ändert sich die Situation des Gefangenendilemmas entscheidend: Die Spieler sollten in der ersten Runde kooperieren, indem sie leugnen, um die niedrigste Strafe für beide zu erzielen. Wenn jedoch einer versucht, den anderen hereinzulegen, indem er gesteht, wird er in der nächsten Runde schlecht abschneiden. Der „Reingelegte“ wird dann die ausbeuterische Taktik des Mitspielers einschlagen und auch gestehen, da er sich nicht auf ihn verlassen kann (tit for tat). Daher wird sich mit großer Wahrscheinlichkeit eine dauerhafte Kooperation entwickeln (beide leugnen), und das Dilemma löst sich auf. Voraussetzung dafür ist, daß die beteiligten Partner einander wiedererkennen können und die Zahl der noch bevorstehenden Runden unbekannt ist, sonst würde die letzte Runde, auf die keine Revanche mehr folgen kann, entsprechend den Regeln des oben beschriebenen einfachen Gefangenendilemmas ablaufen, d.h., jeder würde die ausbeuterische Taktik „Gestehen“ einschlagen. Von R. Axelrod und W.D. Hamilton wurde das Gefangenendilemma in die Verhaltensökologie eingeführt, um die bis dato ungeklärte Entstehung von Kooperation im Tierreich zu untersuchen. Die Auszahlung (pay-off) bezieht sich hier auf das Überleben und die Zahl der Nachkommen der beteiligten Individuen. Das Prinzip des Gefangenendilemmas konnte seither erfolgreich zur Erklärung von evolutionsstabilen Verhaltenstaktiken verwendet werden, welche – gemessen an der absoluten Fitness der beteiligten Individuen – nicht zu verstehen sind, weil sie einen geringeren Fortpflanzungserfolg für die betroffenen Individuen mit sich bringen.
G.U.
Lit.:Luce, R.D. & Raiffa, H. (1957): Games and decisions. Wiley, New York. Rapoport, A. & Chammah, A. (1965): Prisoner's Dilemma. Univ. Michigan Press. Ann Arbor. Axelrod, R. & Hamilton, W.D. (1981): The evolution of cooperation. Science 211: 1390–1396.
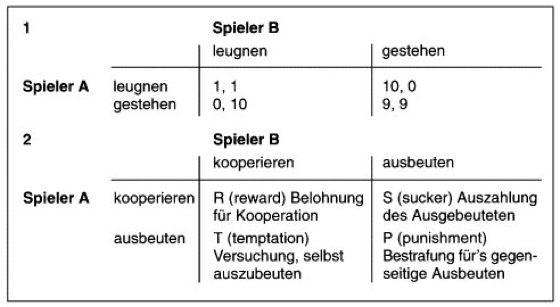
Gefangenendilemma
1 Anzahl der Jahre, die im Gefängnis verbracht werden müssen. Die Zahl vor dem Komma bezieht sich auf Spieler A, die Zahl danach auf Spieler B.
2 Verallgemeinerte Auszahlungsmatrix aus der Sicht des Spielers A nach Axelrod & Hamilton 1981. Bedingungen für das Gefangenendilemma sind:
T>R>P>S und R>(S+T)/2
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.