Basierend auf den Untersuchungen von August Ferdinand Möbius definieren wir für n ≥ 2 die Gruppe M(n)derMöbius-Transformationendern-dimensionalen Sphäre Sⁿ – oder kurz die Möbius-Gruppe – als Menge derjenigen Diffeomorphismen von Sⁿ, die Hypersphären wieder in Hypersphären überführen. Die Gruppenoperation ist dabei durch die Verknüpfung von Abbildungen gegeben. Im Sinne des Erlanger Programms beschreibt die Möbius-GeometriedieWirkungderMöbius-Gruppeüber Sⁿ.

Wir betrachten nun die Sphäre

\begin{eqnarray}{\text{S}}^{n}=\{x\in {{\mathbb{R}}}^{n+1}|x=1\}.\end{eqnarray}

Halten wir auf dem umgebenden ℝⁿ⁺¹ die Standardmetrik fest, so induziert diese eine Metrik und damit eine konforme Struktur auf Sⁿ. Die sicherlich wichtigste strukturelle Beobachtung im Kontext der Möbius-Gruppe ist die Tatsache, daß für alle n ≥ 2 die Möbius-Gruppe mit der Gruppe 𝒞(Sⁿ) der konformen Diffeomorphismen von Sⁿ zusammenfällt und zur globalen Definition einer Abbildung ϕ ∈ ℳ(n) deren Kenntnis auf einer offenen, zusammenhängen Teilmenge U ⊆ Sⁿ genügt. Interessant ist, daß die Begründung dieser Festellungen von der Dimension n abhängt.

Betrachten wir zunächst den Fall n ≥ 3. Aus der Untermannigfaltigkeitentheorie der Riemannschen Geometrie wissen wir, daß im ℝⁿ die offenen Teilmengen von Hypersphären und Hyperebenen die einzigen total umbilischen Hyperflächen sind. Da die Eigenschaft einer Hyperfläche, nur aus umbilischen Punkten zu bestehen, aber eine konforme Invariante ist, ist die konforme Gruppe 𝒞(Sⁿ) in der Möbiusgruppe ℳ(n) enthalten. Andererseits können wir für Sⁿ, so wie für jede konform flache Mannigfaltigkeit, in der Umgebung eines gewählten Punktes x ∈ Sⁿ einen Atlas finden, in dessen lokalen Koordinaten das Differential dϕ |_x eines gegebenen Diffeomorphismus ϕ ∈ M(n), ϕ(x) = x Diagonalgestalt hat. Da dϕ |_x so wie ϕ selbst Hypersphären erhalten muß, ergibt sich die Gleichheit der Eigenwerte von dϕ |_x, dϕ |_x ist eine Homothetie und damit ϕ ein konformer Diffeomorphismus.

Zum Beweis der zweiten Feststellung verweisen wir auf das Liouville-Theorem. Danach existiert für einen auf offenen, zusammenhängenden Teilmengen U, V ⊂ Sⁿ, n ≥ 3 definierten konformen Diffeomorphismus ϕ : U → V stets eine wohldefinierte Fortsetzung \(\hat{\varphi }:{\text{S}}^{n}\to {\text{S}}^{n}\), ϕ ∈ ℳ(n).

Im speziellen Fall n = 2 fallen die Gruppe 𝒞(S²) der global definierten konformen Diffeomorphismen von S² und die Möbius-Gruppe ℳ(n) derjenigen Diffeomorphismen von S², die Kreise wieder in Kreise überführen, ebenfalls zusammen. Eine auf einer offenen, zusammenhängenden Umgebung U ⊂ S² definierte konforme Abbildung kann aber durchaus verschiedene (holomorphe oder antiholomorphe) Fortsetzungen auf der entsprechenden Riemannschen Fläche haben, aber nur diejenigen Fortsetzungen, die sich global auf S² fortsetzen lassen, erhalten auch Kreise.

Wir bemerken an dieser Stelle, daß in Verallgemeinerung der klassischen Begriffsbildungen für konform flache Mannigfaltigkeiten der Begriff einer Möbiusstruktur erklärt werden kann. Ist nämlich M eine konform flache Mannigfaltigkeit und A ein zulässiger Atlas aus lokal konformen Diffeomorphismen in den ℝⁿ, so können wir durch stereographische Projektion diese Abbildungen in Sⁿ verlängern. Eine Möbius-Struktur ist dann ein maximaler Atlas solcher lokaler Diffeomorphismen, für die die entsprechenden Koordinatentransformationen nach stereographischer Projektion Möbius-Transformationen entsprechender offener Mengen in Sⁿ sind. Eine differenzierbare Mannigfaltigkeit mit einer Möbius-Struktur wird auch Möbius-Mannigfaltigkeit genannt.

Für die Wirkung der Möbius-Gruppe über Sⁿ lassen sich verschiedene Modelle einführen. Exemplarisch wollen wir hier ein bereits im vorigen Jahrhundert eingeführtes und von Wilhem Blaschke im ersten Drittel des 20. Jahrhunderts ausführlich beschriebenes Modell betrachten. Der entscheidende Vorteil dieser Modellbildung liegt in der Einbettung der Diffeomorphismengruppe ℳ(n) in gut beschreibbare Gruppen linearer Abildungen. Sei dazu im ℝⁿ⁺² mit Standardkoordinaten

\begin{eqnarray}{J}^{n+1}=\{x\in {{\mathbb{R}}}^{n+2}|{\langle x,x\rangle }_{M}=0\},\end{eqnarray}

wobei ⟨ .,. ⟩_M durch

\begin{eqnarray}{\langle x,y\rangle }_{M}={x}_{0}{y}_{0}+{x}_{1}{y}_{1}+\cdots +{x}_{n+1}{y}_{n+1}\end{eqnarray}

definiert sein soll. Wir setzen Sⁿ = Jⁿ⁺¹/∼, dabei soll x ∼ y genau dann gelten, wenn x = λy für ein λ ∈ ℝ, λ ≠ 0 erfüllt ist. Durch stereographische Projektion kann ein Diffeomorphismus zu der oben beschriebenen Standardeinbettung von Sⁿ in den ℝⁿ⁺¹ konstruiert werden. In dieser Situation ist eine Hypersphäre von Sⁿ wohldefiniert durch die Projektion der Schnittmenge eines (n + 1)-dimensionalen Unterraumes U des ℝⁿ⁺² entlang ∼, wobei

\begin{eqnarray}U=\left \{x\in {{\mathbb{R}}}^{n+2}|\begin{array}{c}\exists y{\in }{{\mathbb{R}}}^{n+2}\\ {\langle y,y\rangle }_{M}=1\,\text{}und\,{\langle x,y\rangle }_{M}=0\end{array}\right\},\end{eqnarray}

und wir können die homogenen Koordinaten des von y erzeugten eindimensionalen Unterraums des ℝⁿ⁺² zur Beschreibung der so definierten Hypersphäre nutzen. Ein Diffeomorphismus ϕ von Sⁿ ist in diesem Modell genau dann eine Möbius-transformation, wenn er durch einen Automorphismus des ℝⁿ⁺² erzeugt wird, der die Menge dieser, die Hypersphären erzeugenden (n + 1)-dimensionalen Unterräume respektiert, es ergibt sich in diesem Modell eine Realisierung der Möbius-Gruppe inner-halb der Invarianzgruppe O(1, n + 1) der Bilinear-form ⟨, ⟩_M auf dem ℝⁿ⁺². Wir bemerken, daß in den klassischen Arbeiten hier vor allem in der Dimension n = 2 gearbeitet wird, die Koordinaten, die sich aus dieser Modellbildung ergeben, werden dort mitunter als tetrazyklische Koordinaten bezeichnet.

Für n = 2 können wir die Möbius-Geometrie in einem weiteren Modell betrachten, das sich aus einem – ebenfalls schon klassisch untersuchten – funktionentheoretischen Kontext ergibt. Sei dazu \(\hat{{\mathbb{C}}}={\mathbb{C}}\cup \{\infty \}\) die komplexe Ebene vereinigt mit dem unendlich fernen Punkt. Die oben bereits benutzte stereographische Projektion liefert eine bijektive Abbildung der Standardeinbettung von S² auf \(\hat{{\mathbb{C}}}\). Die Kreise der Sphäre werden dabei auf die Kreise und Geraden der komplexen Ebene abgebildet, wir betrachten die Geraden hier ebenfalls als Kreise. Die Gruppe

\begin{eqnarray}\text{SL}(2,{\mathbb{C}})= \left\{\left(\begin{array}{cc}a & c\\ b & d\end{array}\right)|\begin{array}{c}a,b,c,d\in {\mathbb{C}}\\ ad-bc=1\end{array}\right\}\end{eqnarray}

wirkt auf ℂ \ z₀, cz₀ + d = 0 durch

\begin{eqnarray}\left(\begin{array}{cc}a & c\\ b & d\end{array}\right)z=\displaystyle \frac{az+b}{cz+d}.\end{eqnarray}

Jede solche Abbildung erhält Kreise in der komplexen Ebene, daher gibt es, wie oben ausgeführt, genau eine auf ganz S² definierte Möbius-Transformation, deren Einschränkung auf ℂ \{z₀} durch obenstehende Wirkung definiert ist und für die darüber hinaus z₀ auf ∞ abgebildet wird. Der Nichteffektivitätskern dieser Wirkung ist {± I}, dies liefert ℳ(2) ∼= SL(2, ℂ)/{± I}. Dieses Modell der Möbius-Geometrie ist auch die Grundlage der hyperbolischen Geometrie der Ebene sowie der weit entwickelten Theorie der Fuchsschen Gruppen, hier ergibt sich eine wichtige Verbindung zur Theorie der Riemannschen Flächen.

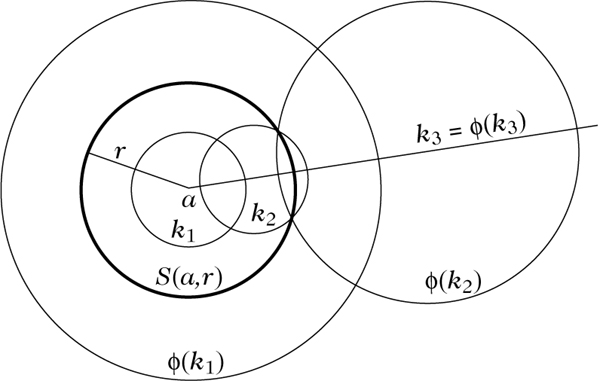
Zu den wichtigsten Eigenschaften der Möbius-Gruppe zählt ihre endliche Erzeugbarkeit aus elementar definierbaren Spiegelungen an Hyper-sphären, den Inversionen. Wir können diese Inversionen einführen, indem wir Sⁿ stereographisch in den ℝⁿ projizieren und dort die Inversion ϕ an der Sphäre S(a, r) um a ∈ ℝⁿ mit dem Radius r ∈ ℝ, r > 0, definiert durch

\begin{eqnarray}S(a,r)=\{\begin{array}{cc}x\in {R}^{n}| & ||x-a||=r\end{array}\},\end{eqnarray}

durch

\begin{eqnarray}\varphi (x)=a+{\left(\frac{r}{||x-a||}\right)}^{2}(x-a),x\in {{\mathbb{R}}}^{n}\end{eqnarray}

bestimmen. Auf der Grundlage dieser Eigenschaft wurde die Möbius-Geometrie in der Vergangenheit auch immer wieder als Inversionsgeometrie bezeichnet.

Den Intentionen des Erlanger Programms folgend wurde in der ersten Hälfte des 20. Jahrhunderts vor allem die Invariantentheorie der Wirkung der Möbius-Gruppe über S² und S³ entwickelt. Dabei wird hier vor allem die durch ℳ(n) induzierte Wirkung auf den Hypersphären in den Vordergrund gestellt. Nach dem Aufbau von Invarianten endlicher Mengen von Hypersphären werden von Blaschke dann Invariantensysteme für einparametrige Scharen von Hypersphären entwickelt. Diese Systeme entsprechen den Frenet-Formeln der Kurventheorie in der Riemannschen Geometrie des ℝⁿ. In moderneren Untersuchungen spielt die MöbiusGeometrie vor allem durch die oben bereits angesprochenen Verbindungen zur Theorie der Riemannschen Flächen oder zur Untermannigfaltigkeitentheorie im Rahmen der Riemannschen und konformen Geometrie eine wichtige Rolle.

Literatur

[1] Blaschke,W.: Vorlesungen über Differentialgeometrie III. Verlag von Julius Springer Berlin, 1929.

[2] Beardon,A.F.: The Geometry of Discrete Groups. Springer Verlag New York, 1983.

[3] Kulkarni,R.S.; Pinkall,U.: Conformal Geometry. Friedr. Vieweg & Sohn Braunschweig, 1988.