eine ganze Zahl der Form \begin{eqnarray}\omega (n)=\frac{1}{2}(3{n}^{2}-n),\,\,\,\,\,\,n\in {\mathbb{Z}}.\end{eqnarray}

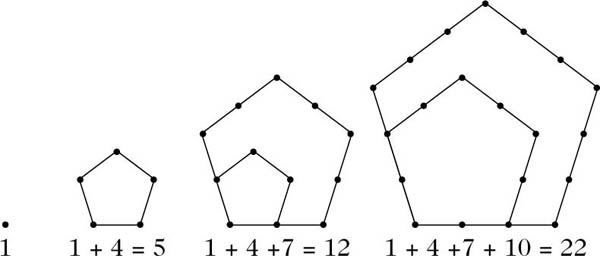
Es gilt ω(0) = 0 und ω(n) ∈ ℕ für n ≠ 0. Einige Beispiele: ω(1) = 1, ω(2) = 5, ω(3) = 12, ω(4) = 22, ω(5) = 35, ω(−1) = 2, ω(−2) = 7, ω(−3) = 15, ω(−4) = 26, ω(−5) = 40.

Die Bezeichnung Pentagonal-Zahl hat folgenden geometrischen Hintergrund. Legt man regelmäßige Fünfecke der Kantenlängen 1, 2, 3,… ineinander und zählt die Anzahl der „Eckpunkte“, so erhält man die Folge (ω(n))_n∈ℕ.