Lexikon der Mathematik: serieller Addierer
sequentieller logischer Schaltkreis zur Durchführung der Addition \(s=({s}_{n-1},\mathrm{\ldots},{s}_{0})\) von zwei n-stelligen binären Zahlen \(\alpha =({\alpha}_{n-1},\mathrm{\ldots},{\alpha}_{0})\) und \(\beta =({\beta}_{n-1},\mathrm{\ldots},{\beta}_{0})\), der n Schritte benötigt, um das Ergebnis bereitzustellen.
Im ersten Schritt wird das nullte Summenbit so \({s}_{0}={\alpha}_{0}\oplus {\beta}_{0}\) und der an dieser Stelle auftretende Übertrag \({c}_{0}={\alpha}_{0}\wedge {\beta}_{0}\) berechnet. Im (i + 1)-ten Schritt (1 ≤ i< n − 1) wird das i-te Summenbit \({s}_{i}={\alpha}_{i}\oplus {\beta}_{i}\oplus {c}_{i-1}\) und der an der i-ten Stelle auftretende Übertrag
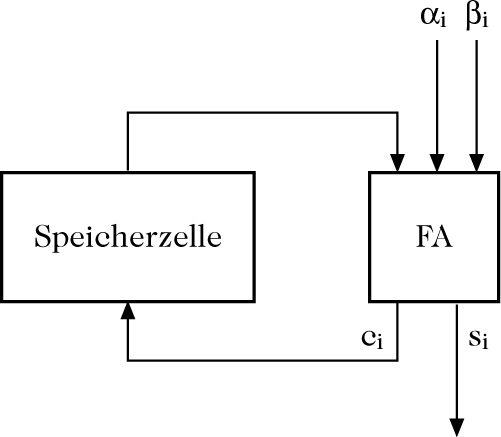
Serieller Addierer
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.