Beugungseffektivität, Effizienz, der Anteil η des auf ein Beugungsgitter auffallenden Lichtes, der in eine bestimmte Beugungsordnung gebeugt wird. Bei Reflexionsgittern bezieht sich die absolute B. auf den direkten Vergleich mit dem einfallenden Licht, die relative B. auf den Vergleich mit dem an einem Metallspiegel, der aus dem gleichen Material wie die Gitterbeschichtung besteht, reflektierten Licht. Die B. von Sinusgittern (d.h. Gittern mit sinusförmigem Furchenprofil) sind ein Hinweis auf den Lichtanteil, der in das rekonstruierte Bild eines Hologramms (Holographie) gelangt, da der Bildinhalt beim Hologramm über eine Superposition von Sinusgittern codiert ist. Für gitterspektroskopische Geräte ist die B. ebenfalls eine wichtige Kennzahl. Bei Oberflächenrelief-Phasengittern (sowohl in Transmission als auch in Reflexion) unterscheidet man je nach der Größe des Quotienten aus Modulationstiefe h, d.h. der Tiefe der Gitterfurchen (im Sinne der optischen Weglänge), und Gitterkonstanten g flache (h/g≈0,05) oder tiefe (h/g

0,1) Gitter. Bei dünnen Absorptions- und Phasengittern sowie flachen Oberflächenreliefgittern hängt die B. nur wenig von der Polarisationsrichtung des einfallenden Lichtes – elektrischer Feldstärkevektor E parallel (E_||) oder senkrecht (E⊥) zu den Gitterfurchen – ab. Man spricht daher von dem skalaren Fall.

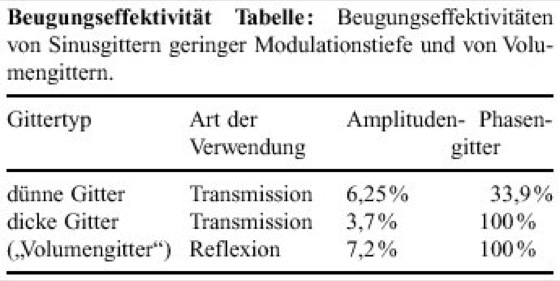
Für die genannten Gitter gelten die in der Tabelle aufgeführten Werte der B. Die hohen Effektivitäten für Volumenphasengitter kommen durch Modenkopplung zwischen einfallender und gebeugter Welle zustande. Es zeigt sich, daß Phasengitter bedeutend wirkungsvoller als Amplitudengitter sind.

Flache Phasengitter können bedeutend höhere B. als die in der Tabelle angegebenen aufweisen, wenn von den Sinusgittern zu den geblazten Gittern mit asymmetrischen dreieckförmigen Furchen übergegangen wird. Tiefe Gitter wie z.B. Oberflächen-Relief-Phasengitter in Reflexion, also die üblichen mit Metall verspiegelten Gitter, können nahezu eine B. von 100% erreichen. Die für die B. wichtigen Größen eines Gitterprofils sind h/g (s.o.) und λ/g, wobei λ die Lichtwellenlänge bezeichnet. Abbildung 1 macht deutlich, daß für flache Gitter der skalare Fall, für tiefe Gitter dagegen der elektromagnetische oder vektorielle Fall vorliegt, in dem die B. stark von der Polarisationsrichtung des einfallenden Lichtes abhängt. Insbesondere treten mit wachsendem Verhältnis h/g bei senkrechter Polarisation des Lichtes (E⊥) große Werte der B. über einen weiten Wellenlängenbereich der Größenordnung Δλ≈g auf. Für praktische Anwendungen ist die Wahl 0,2<h/g<0,3 günstig. Die Pfeile in Abb. 1 zeigen λ/g-Werte, an denen die Woodschen Anomalien auftreten können. Dort führt eine Änderung von λ zu einer solchen Änderung des Beugungswinkels, daß sich das Licht einer bestimmten Beugungsordnung nicht mehr in den freien Raum, sondern längs der Gitteroberfläche ausbreitet. Die betreffende Beugungsordnung erscheint dann nicht mehr in der Energiebilanz, und es können Schwankungen im Effektivitätsverlauf (als Funktion von λ) auftreten. Damit können nicht vorhandene Spektrallinien vorgetäuscht werden. Weitere Anomalien treten bei Anregung von Oberflächenplasmonen in Gittern durch die einfallende Strahlung in Erscheinung. Für 0,6<λ/g<2 ist in Littrow-Aufstellung die 1. Beugungsordnung die einzige gebeugte Ordnung. Es treten keine Anomalien auf, und die Gitter sind vorteilhaft einzusetzen. In diesem Bereiche hat auch die genaue Furchenform keinen allzu großen Einfluß auf die B.

Geblazte Profile (geblaztes Gitter) werden bevorzugt, wenn sich die Wellenlänge des zu untersuchenden Lichtes über mehr als eine Oktave erstreckt. Hohe B. über 90% können nicht nur mit Metallreflexions-Sinusgittern mit h/g≈0,3 erreicht werden, sondern auch mit Transmissions-Phasen-Sinusgittern mit h/g≈1,5 bis 2, was etwa gleichen Phasendifferenzen der durch das Profilminimum bzw. -maximum hindurchgegangenen Strahlen entspricht.

Durch Aufbringen verstärkender Schichten (d.h. Schichten, in denen eine Besetzungsinversion erzeugt wurde) auf verspiegelte Gitter läßt sich Verstärkung einfallender Strahlung in verschiedenen Beugungsordnungen erreichen.

Gitterbeschichtungen ändern den Effektivitätsverlauf. So führen Wellenausbreitungen in Deckschichten zu speziellen Filterwirkungen.

Die Interferenzen in der Schicht oder in Schichtsystemen können in vorgegebenen Wellenlängenbereichen zur Anhebung der Effektivität verwendet werden. Ein Beispiel sind die zusätzlichen Effektivitätsmaxima geblazter Gitter im Infraroten.

Theorien zur Berechnung der B. Für flache Gitter führt die Kirchhoffsche Beugungstheorie oder ein Anpassen der in die Furchen fortgesetzten einfallenden und der gebeugten Felder aneinander auf der Furchenoberfläche nach Rayleigh zu den wesentlichen Merkmalen der Effektivitätsverläufe.

Für Volumengitter schwacher Modulation reicht die erste Bornsche Näherung der Streutheorie aus, also eine Addition der von den einzelnen Volumenelementen ausgehenden Kugelwellen im Fernfeld, wobei die Amplituden der Kugelwellen entsprechend der Brechungsindexmodulation im Volumen variieren. Bei starker Modulation ist die Methode der gekoppelten Wellen (nach H. Kogelnik) erfolgreich, wobei jeder von der Braggschen Reflexionsbedingung zugelassenen Ausbreitungsrichtung eine beim Durchgang durch das Medium variierende Amplitude zugeordnet wird. Im einfachsten Falle gehorchen die (komplexe) Amplitude R der ungebeugt durch das Phasengitter hindurchgehenden Welle (in der Holographie Rekonstruktionswelle genannt) und die Amplitude S der in 1. Ordnung gebeugten Welle (Signalwelle) dem Differentialgleichungssystem

dR/dz=-iκS, dS/dz=-iκR, (1)

wobei die Konstante κ proportional zu der Amplitude der Brechungsindexvariation im Phasengitter ist. Die Anfangsbedingungen für (1) lauten in zweckmäßiger Normierung R(0)=1, S(0)=0. An Hand der Lösung erkennt man (Abb. 2), daß an einer bestimmten Stelle z=z_max sich die gesamte eingestrahlte Energie in der gebeugten Welle wiederfindet, so daß die B. η=1 erreicht wird, wenn man als Gitterdicke den Wert z_max wählt. Macht man das Gitter jedoch dicker, so geht die Energie z.T. in die Rekonstruktionswelle zurück.

Oberflächenreliefgitter werden gegenwärtig mit verschiedenen Methoden behandelt:

- Integralgleichungen (D. Maystre 1971) und Integralgleichungssysteme (B. Kleemann, A. Pomp 1985) können formuliert werden, indem gesuchte Dipol- und Monopolschichten auf der Furchenoberfläche angenommen und die Erfüllung der Übergangsbedingungen der Maxwellschen Theorie für die Felder gefordert wird.

- Differentialgleichungssysteme (R. Petit, M. Neviere, P. Vincent) werden abgeleitet für miteinander gekoppelte Moden, wobei die von den Furchen zwischen Maximum und Minimum gebildete Schicht als inhomogenes Medium aufgefaßt wird und alle die Felder und das inhomogene Medium beschreibenden Funktionen bezüglich der Koordinate in der zu den Gitterfurchen senkrechten Richtung als Überlagerungen periodischer Funktionen (z.B. "Beugungsordnungen") angesetzt werden. Die Amplituden dieser periodischen Funktionen genügen einem gekoppelten Differentialgleichungssystem, das die Ausbreitung senkrecht zur Gitteroberfläche beschreibt.

- Die RCWA-Methode (Rigorous Coupled Wave Analysis, M. G. Moharam, T. K. Gaylord) stellt eine Weiterentwicklung von (1) für viele Moden unter Entwicklung der Brechungsindexvariation im Gitterfurchenbereich nach harmonischen Funktionen dar.

- Modenentwicklungen unter Berücksichtigung der durch die Gitterfurchen gegebenen Randbedingungen führen für spezielle Furchenprofile zu exakten Lösungen (BKK-Methode; C. B. Burghardt, S. G. Kaspar, K. Knop 1978).

Auch räumlich diskretisierende numerische Verfahren (Beugungstheorie) finden zunehmend Anwendung. Gegenwärtig können beliebige Furchenprofilformen und Beschichtungen mit einer dem Experiment vergleichbaren Genauigkeit behandelt werden.

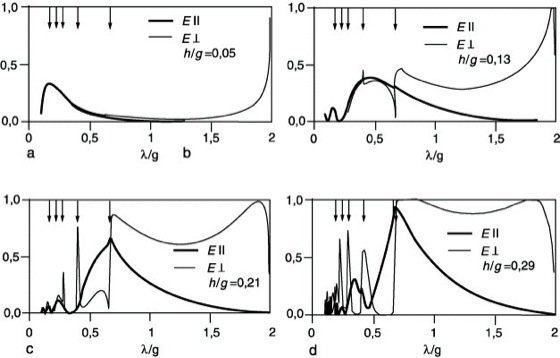
Beugungseffektivität 1: Für unendlich gut leitendes Gittermaterial berechnete Werte der Beugungseffektivität η von Sinusgittern in Littrow-Aufstellung als Funktion von λ/g für verschiedene Werte des Parameters h/g (λ Wellenlänge, g Gitterkonstante, h Modulationstiefe, E⊥ und E_|| elektrische Feldstärke senkrecht bzw. parallel zu den Gitterfurchen): a) h/g = 0,05, b) h/g = 0,13, c) h/g = 0,21, d) h/g = 0,29. Die Pfeile bezeichnen die Wellenlängen, bei denen Gitteranomalien vorliegen (nach B. Kleemann, Berlin).

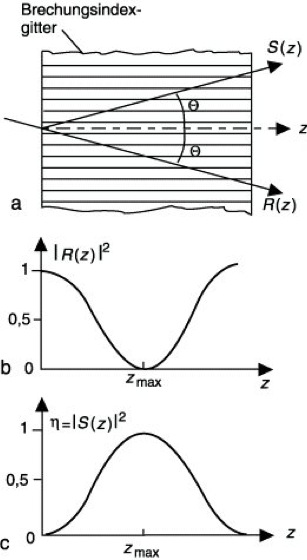
Beugungseffektivität 2: Wellenkopplung im Transmissionsphasengitter. a) Darstellung der Bragg-Reflexion, b) Intensitätsverlauf der ungebeugten Welle und c) der gebeugten Welle (Beugungseffektivität).