Holographie, ein wellenoptisches Aufzeichnungs- und Wiedergabeverfahren, das die Erzeugung echt räumlicher Bilder ermöglicht. Sie wurde in den Jahren 1948 bis 1951 von D. Gabor entwickelt und später von E.N. Leith und J. Upatnieks sowie von G.W. Stroke und Ju.N. Denisjuk vervollkommnet.

Zum Durchbruch gelangte die H. erst, als mit dem Laser eine kohärente Lichtquelle ausreichender Intensität zur Verfügung stand.

Der Vorgang der Hologrammaufnahme besteht darin, daß man das von einem Objekt beeinflußte Wellenfeld mit einer Referenzwelle (dem kohärenten Untergrund) überlagert und das dabei entstehende Interferenzmuster photographiert. Wird ein Objekt mit kohärentem Licht beleuchtet, so enthält das vom Gegenstand durch Reflexion, Transmission, Beugung oder Streuung beeinflußte Wellenfeld in seiner Amplituden- und Phasenverteilung (unter Umständen auch in seiner Frequenz und seinem Polarisationszustand) die optisch erfaßbare Information über das Objekt. In der Hologrammebene (z.B. x-y-Ebene) ist dieses Wellenfeld durch eine charakteristische Amplituden- und Phasenverteilung gekennzeichnet.

Für die komplexe Amplitude der Objektwelle schreiben wir

dabei bezeichnet A_O die reelle Amplitude und ϕ_O die Phase. Entsprechend gilt für die komplexe Amplitude der Referenzwelle


.

Im Ergebnis der Überlagerung dieser beiden Wellenfelder registriert ein in der x-y-Ebene angeordneter quadratischer Empfänger die Intensitätsverteilung


(1)

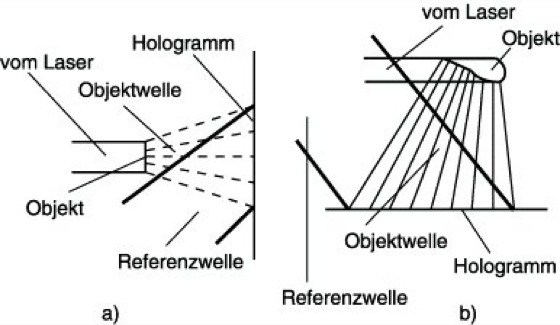
Abb. 1 zeigt eine Anordnung zur Aufnahme eines punktförmigen Objektes. Da die Richtung der Referenzwelle und die mittlere Richtung der Objektwelle zusammenfallen, spricht man von Geradeausholographie, auch in-line- oder Gabor-Verfahren genannt.

Das vom Laser kommende Licht bildet nach Passieren der Linsen 1 und 2 sowie einer Lochblende eine ebene Wellenfront (Referenzwelle), die auf ein punktförmiges Objekt trifft, von dem wiederum eine Kugelwelle (die Objektwelle) ausgeht.

In der Hologrammebene interferieren die beiden Wellen miteinander und das dabei entstehende Interferenzmuster wird aufgezeichnet (photographiert). Nach dem Entwickeln und Fixieren der Photoplatte liegt das Hologramm, das in unserem Falle einer Fresnelschen Zonenplatte entspricht, vor.

Auf ein Ensemble von Punkten oder ein Objekt läßt sich eine ähnliche Betrachtung anwenden. Das Hologramm entsteht durch die Überlagerung entsprechend vieler Zonenfiguren. Da die Strukturierung innerhalb des Interferenzbildes sehr fein ist (z.T. feiner als die Wellenlänge des zum Aufzeichnen benutzten Lichtes), muß das zum Aufzeichnen des Hologramms verwendete optische Speichermaterial ein hohes Auflösungsvermögen (2000 bis 3000 Linien/mm) besitzen.

Die Eigenschaften des optischen Aufzeichnungsmaterials haben einen großen Einfluß auf die holographische Übertragung. Ein Vorteil der holographischen Objektdarstellung besteht u.a. darin, daß sich das für das Objekt charakteristische Interferenzmuster über die gesamte Speicherfläche (Photoplatte) verteilt und nicht lokal begrenzt ist. Entsprechend lassen sich alle Informationen über das ursprüngliche Objekt auch aus Teilen eines Hologramms gewinnen, wobei der Rauschpegel allerdings ansteigt.

Neben der Geradeausholographie ist die Trägerfrequenzholographie (off-axis-Verfahren) von großer praktischer Bedeutung. Dabei bildet die Richtung der Referenzwelle einen Winkel mit der mittleren Richtung der Objektwelle (Abb. 2). Hier handelt es sich um einen der Modulation vergleichbaren Effekt. Auf die durch den Winkel zwischen dem gebeugten Objektlicht und der Referenzwelle sowie durch die Wellenlänge gegebene Trägerfrequenz (Ortsfrequenz) wird die Objektinformation (gebeugter Objektlichtanteil) aufmoduliert.

Im Zusammenhang mit der Hologrammrekonstruktion wird vereinfachend angenommen, daß die Amplitudentransmission T_A der entwickelten Hologrammplatte der gespeicherten Intensitätsverteilung I proportional ist (T_A~I). Ein die Hologrammplatte durchsetzendes kohärentes Wellenfeld besitzt, wenn die einfallende Welle, die sogenannte Rekonstruktionswelle mit der komplexen Amplitude C, vereinfachend als identisch mit der Referenzwelle B angenommen wird, nach (1) die komplexe Amplitude


. (2)

Der vorletzte Term in (2) enthält die komplexe Amplitude O der Objektwelle als Faktor und liefert somit ein virtuelles, dem Objekt entsprechendes Bild. Der letzte Term in (2) enthält die konjugierte Amplitude O* der Objektwelle, die einem reellen Bild entspricht (Abb. 3).

Die Bilder erscheinen im wesentlichen in der +1. und -1. Beugungsordnung und sind beim off-axis-Verfahren richtungsmäßig getrennt.

Das virtuelle Bild entspricht optisch vollkommen dem Objekt (hinsichtlich der räumlichen Tiefe und der parallaktischen Erscheinungen) und kann durch das Hologramm hindurch mit einer Kamera aufgenommen werden.

Das reelle Bild ist ebenfalls echt räumlich, jedoch im allgemeinen pseudoskopisch, d.h., die Tiefenverhältnisse sind gegenüber denen des Objektes invertiert. Das reelle Bild kann ohne optische Hilfsmittel auf einem Film registriert werden.

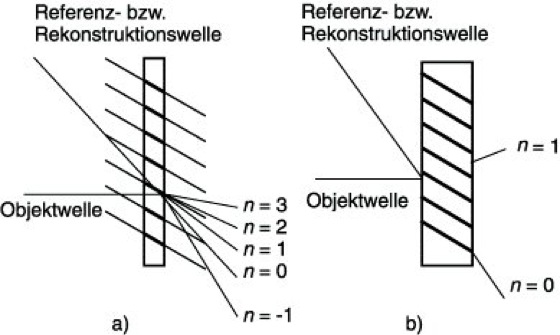
Die Hologrammaufzeichnung kann sowohl in dünnen lichtempfindlichen Schichten (ebenes Hologramm) als auch in lichtempfindlichen dicken Medien (Volumenhologramm) erfolgen. Bei der Herstellung von Hologrammen spielt die Dicke des verwendeten Speichermaterials eine wichtige Rolle. Den Unterschied zwischen ebenen und Volumenhologrammen erläutert Abbildung 4 für den Fall des Einspeicherns einer ebenen Welle mit Hilfe einer ebenen Referenzwelle. Objekt- und Referenzwelle bilden ein räumlich stehendes Interferenzmuster, das vom optischen Speichermedium (Hologramm) registriert wird. Bei der Rekonstruktion werden beide Hologrammtypen mit der ursprünglichen Referenzwelle rekonstruiert.

Das ebene Hologramm fügt zur hindurchgehenden nullten Beugungsordnung (n=0) die verschiedenen Beugungsordnungen hinzu, die auch bei einem normalen ebenen Gitter zu erwarten sind. Die erste Beugungsordnung (n=1) stellt das rekonstruierte Bild, hier die rekonstruierte ebene Welle, dar. Im Volumenhologramm hingegen wird nach dem Gesetz der Bragg-Reflexion neben der nullten Beugungsordnung nur die +1. oder die -1. Beugungsordnung erzeugt. Ein dickes optisches Speichermedium bietet den Vorteil, daß in ihm mehrere Interferenzstrukturen überlagert werden können; das Volumenhologramm besteht dann aus vielen superponierten Interferenzstrukturen. Durch Einhaltung bestimmter Winkel bzw. Wellenlängen bei der Rekonstruktion kann Bild für Bild aus dem Volumenhologramm rekonstruiert werden (s.u.).

Neben dem oben geschilderten Amplitudenhologramm, bei dem das Interferenzmuster als Schwärzungsverteilung aufgezeichnet wird (das Hologramm moduliert über die Extinktion die Rekonstruktionswelle) gibt es auch das Phasenhologramm, bei dem das Interferenzmuster in Form eines Oberflächenreliefs oder einer Brechzahlverteilung innerhalb des Mediums gespeichert wird. Das Hologramm beeinflußt dann die Phase der Rekonstruktionswelle.

Von Fraunhofer-Holographie wird dann gesprochen, wenn der Abstand zwischen dem Objekt und dem Hologramm groß gegen die Objektdimension ist. Bei der Fourier-Holographie besteht das Grundprinzip darin, daß das Hologramm die Fourier-Transformierte der Objektfunktion registriert (optische Bildverarbeitung). Mit der Rekonstruktion eines solchen Hologramms wird eine Fourier-Rücktransformation durchgeführt. Der Prozeß der holographischen Aufnahme und Rekonstruktion läßt sich als ein Abbildungsvorgang auffassen. Ist das Hologramm in der x-y-Ebene angeordnet, so lauten die Abbildungsgleichungen für den einfachen Fall, daß Objekt-, Referenz und Rekonstruktionslichtquelle punktförmig auf der z-Achse angeordnet sind,


(3)

Dabei bedeuten z_Bv und z_Br die Koordinate des virtuellen bzw. des reellen Bildpunktes, z_O die Objektkoordinate, z_R und z_C die Koordinate der Referenz- bzw. der Rekonstruktionslichtquelle. Der Koordinatenursprung liegt in der Hologrammebene. Die Gleichungen müssen erweitert werden, falls zur Aufnahme und Rekonstruktion unterschiedliche Wellenlängen verwendet werden oder das Hologramm vergrößert oder verkleinert wird (scaling-up).

Auch die holographische Abbildung ist mit Abbildungsfehlern behaftet, die unter Einhaltung bestimmter Bedingungen korrigiert werden können. Komplette Anordnungen zur Hologrammaufnahme und -wiedergabe, bestehend aus Lasern, optischen Bauelementen und einer stabilen Grundplatte, werden als Hologrammkameras bezeichnet.

Durch geeignete Wahl der Aufnahme- und der Rekonstruktionsparameter können die Abbildungsmaßstäbe von reellem und virtuellem Bild in weiten Grenzen geändert werden. So kann man z.B. ein vergrößertes reelles Bild erhalten, was zur holographischen Mikroskopie führt. In der Mikroskopie wird oft ein Hologramm des vergrößerten Zwischenbildes angefertigt, das eine Speicherung der Information über ein räumlich ausgedehntes Objekt ermöglicht (holographische Mikroskopie).

In einem optischen Speichermedium lassen sich durch Mehrfachexposition mehrere Hologramme (z.B. in der Volumenholographie), d.h. die Bilder verschiedener Objekte speichern. Dieser Sachverhalt ist für die Hologramminterferometrie von großer Bedeutung, die die interferometrische Vermessung von geringfügigen Objektveränderungen (Verschiebung, Rotation, Verformung, Spannungen usw.) ermöglicht.

Die Überlagerung mehrerer Hologramme kann bei Verwendung dicker optischer Speichermedien zur holographischen Datenspeicherung genutzt werden. Dabei werden zwei Fälle unterschieden:

a) Objekt- und Referenzwelle schließen einen konstanten Winkel (optimal um 90°) ein, die Hologrammplatte wird nach jeder Exposition um einen bestimmten Winkelbetrag gedreht (Winkelkodierung).

b) Objekt- und Referenzwelle schließen einen konstanten Winkel (optimal um 180°, backside hologram) ein, und für jede Exposition wird eine andere Wellenlänge verwendet (Wellenlängenkodierung).

In beiden Fällen entstehen in der lichtempfindlichen Schicht Systeme von Schwärzungsflächen, die beim Rekonstruktionsprozeß die Erzeugung des dem diskreten Winkelwert bzw. der diskreten Wellenlänge zugeordneten Bildes ermöglichen. Da Objekt- und Referenzwelle in einem reziproken Verhältnis stehen (Einstrahlen der Referenzwelle in das Hologramm erzeugt die Objektwelle und Einstrahlen der Objektwelle erzeugt die Referenzwelle), ist eine holographisch-optische Datenverarbeitung in Form der Zuordnung von Zeichen über das Hologramm möglich.

Auch der in der optischen Bildverarbeitung wichtige Prozeß der optischen Filterung ist z.T. ein holographisches Problem, da die benutzten Filter (matched filter) mit holographischen Methoden hergestellt werden können.

Die Superposition von Hologrammen bzw. die Mehrfachspeicherung in dicken optischen Speichermedien ist Grundlage der Farbholographie. Hierbei werden unter Verwendung von Laserlicht unterschiedlicher Wellenlänge "Farbauszüge" des Objektes in Form von zwei bzw. drei Hologrammen hergestellt, die z.B. auf einer dicken Photoplatte überlagert sein können. Wird Licht der bei der Aufnahme verwendeten Wellenlängen (oder weißes Licht) in das nach dem Entwickeln und Fixieren fertige Hologramm eingestrahlt, so ergibt die additive Mischung der von den Einzelhologrammen erzeugten Bilder das farbige Bild des Objektes.

Führt man bei der Hologrammaufnahme die Referenzwelle durch die Plattenrückseite zu (backside hologram), so entstehen wie im Falle der Wellenlängenkodierung Systeme von Schwärzungsflächen (bei Verwendung einer z.B. 20 μm dicken Photoemulsion), die den einzelnen Farbauszügen entsprechen. Wegen der spektralen Filterwirkung der Schwärzungsflächensysteme (infolge von Bragg-Reflexion) sind derartige Hologramme in Weißlicht rekonstruierbar (Weißlichthologramme).

Die H. basiert auf der Interferenz und der Beugung des Lichtes. Für die Hologrammaufnahme und -rekonstruktion sind prinzipiell keine klassischen optischen Bauelemente wie Linsen oder Prismen erforderlich. H. kann deshalb auch in Wellenlängenbereichen betrieben werden, für die es keine optischen Abbildungselemente gibt (Röntgen- und Ultraschallgebiet).

Holographie 1: Geradeausholographie.

Holographie 2: Holographische Aufnahme mit schräg einfallender Referenzwelle (Trägerfrequenzholographie). a) Durchlicht, b) Auflicht.

Holographie 3: Rekonstruktion eines Hologrammbildes, a) reelles, b) virtuelles Bild. L Lichtquelle, F Filmebene, Br reeller und Bv virtueller Bildpunkt, H Hologramm.

Holographie 4: Unterschied zwischen einem ebenen (a) und einem Volumenhologramm (b). n Beugungsordnung.