Einstein-Koeffizient, für eine Atom- oder Molekülsorte charakteristischer Parameter, der wesentlich die Emissions- bzw. Absorptionsrate (Zahl der in der Zeiteinheit emittierten bzw. absorbierten Photonen) eines Systems von Atomen oder Molekülen bestimmt.

1) spontane Emission: Der E. für spontane Emission A₂₁ gibt die Wahrscheinlichkeit dafür an, daß ein angeregtes Atom bzw. Molekül in der Zeiteinheit spontan ein Photon aussendet, wobei es von einem höheren Energieniveau 2 in ein tieferes Niveau 1 übergeht. Die Ausstrahlung erfolgt bei der Resonanzfrequenz ν_r des atomaren Systems, d.h. bei dem durch das Plancksche Wirkungsquantum h dividierten Niveauabstand. Die spontane Emissionsrate ist dann das Produkt aus A₂₁ und der Zahl der angeregten Teilchen. Der reziproke Wert von A₂₁ ist, falls keine weiteren, vom oberen Niveau ausgehenden Übergänge möglich sind, gleich der mittleren Lebensdauer des Niveaus 2.

2) induzierte Emission: Der E. für induzierte Emission B₂₁ gibt, mit der – an der Resonanzfrequenz ν_r genommenen – auf die Einheit des Frequenzintervalls bezogenen Energiedichte u(ν_r) der bereits vorhandenen (als isotrop vorausgesetzten) Strahlung multipliziert, die entsprechende Wahrscheinlichkeit für induzierte Ausstrahlung eines Photons an.

3) Absorption: Der E. für Absorption B₁₂ gibt, mit u(ν_r) multipliziert, die Wahrscheinlichkeit dafür an, daß ein in einem tieferen Energieniveau 1 befindliches Atom unter Absorption eines Photons in der Zeiteinheit in ein höheres Niveau 2 übergeht.

Aus thermodynamischen Überlegungen wurden von Einstein die folgenden allgemeingültigen Beziehungen hergeleitet: B₂₁=A₂₁c³/(8πhν_r³), wobei c die Lichtgeschwindigkeit bedeutet, sowie B₁₂=(g₂/g₁) B₂₁ mit g₁ und g₂ als Entartungsgrad (Zahl der Unterniveaus) der Niveaus. Man beachte, daß die Zahlenwerte für B₁₂ und B₂₁ von der Wahl der Bezugsgrößen (neben der Energiedichte findet auch die Energiestromdichte Verwendung, wobei die genannten Größen auf die Einheit des Intervalls der Frequenz, der Kreisfrequenz oder der Wellenlänge bezogen werden können) abhängen. Bei gerichteter Strahlung besteht der Zusammenhang

zwischen A₂₁ und dem totalen Absorptionsquerschnitt σ₀ (Absorptionskoeffizient), wobei λ_r die Resonanzwellenlänge λ_r=c/ν_r bezeichnet. Der E. A₂₁ steht weiterhin mit der Oszillatorstärke in Beziehung.

Nach der Quantentheorie ergibt sich für A₂₁ der folgende Ausdruck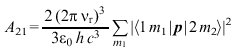

Dabei bedeuten ε₀ die Dielelektrizitätskonstante des Vakuums und p=er (mit e als elektrischer Elementarladung und r als Ortsoperator) den Operator des elektrischen Dipolmomentes. Unter 〈1m₁|p|2m₂〉 ist das quantenmechanische Matrixelement dieses Operators bezüglich des Ausgangszustandes (Niveau 2, Unterniveau m₂) und des Endzustandes (Niveau 1, Unterniveau m₁), das sogenannte Übergangsdipolmoment, zu verstehen. Die Summe erstreckt sich über alle Unterniveaus m₁, sie ist aus Symmetriegründen von m₂ unabhängig.