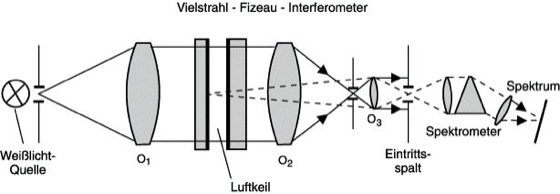
Müllersche Streifen, Streifen gleicher Farbordnung, spektral zerlegte Interferenzerscheinung, die an dünnen durchsichtigen Objekten im weißen Lichte auftritt. Die Bezeichnung M. S. bezog sich ursprünglich nur auf Interferenzerscheinungen an doppelbrechenden Kristallen, die sich zwischen einem Polarisator und einem Analysator befinden, neuerdings wird sie auch auf spektral zerlegte Interferenzen gleicher Dicke bei Weißlichtbeleuchtung angewendet. Die M. S. kommen folgendermaßen zustande: Ein dünnes transparentes Objekt, z.B. ein (reeller oder virtueller) Keil oder ein Film wird mit kollimiertem Weißlicht durchstrahlt. (Genausogut kann die Beobachtung im reflektierten Licht vorgenommen werden.) Das austretende Licht wird einem Spektralapparate zugeführt (Abb. 1). Zu diesem Zwecke wird ein Ausschnitt des Objektes mit einem Objektiv auf den Eintrittsspalt des Spektralapparates abgebildet. Die Phasenbeziehung zwischen den in einem Punkte P' des Spaltes zusammentreffenden Teilstrahlen ist dann die gleiche wie in dem Punkte P auf der Rückseite (Austrittsfläche) des Objektes, dessen Bild P' ist. Je nachdem, welche Dicke das durchstrahlte Objekt an der Stelle P besitzt, ist die Intensität des Lichtes in P' bei gewissen (Vakuum-) Wellenlängen λ₀^(m) maximal. Diese ergeben sich aus der Bedingung, daß der Gangunterschied der zwei interferierenden Strahlen gerade mλ₀^(m) beträgt, wobei m=0,1,2,... die Ordnung der Interferenz angibt. Unterschiedlichen Punkten P' des Spaltes entsprechen so normalerweise unterschiedliche ausgezeichnete Wellenlängen λ₀^(m). Die spektrale Zerlegung des auf den Eintrittsspalt fallenden Lichtes durch den Spektralapparat führt dann zum Auftreten bunter Kurven, der M. S., die das kontinuierliche Spektrum durchziehen (Abb. 2) und jeweils einer bestimmten Ordnung m entsprechen. Sie werden besonders scharf im Falle von Vielstrahlinterferenzen, wie sie bei verspiegelten Oberflächen in Erscheinung treten. Die M. S. eignen sich zur Messung des Oberflächenprofils eines Objektes. Die ausgezeichneten Wellenlängen genügen der Bedingung


,

wobei ϕ einen im allgemeinen wellenlängenabhängigen Phasensprung bei der Reflexion bedeutet. Wenn, in Richtung des Eintrittsspaltes des Spektrographen gesehen, eine Dickenänderung Δd=d₂-d₁ am Keile auftritt, wobei d₁ und d₂ die Keildicken an zwei verschiedenen Stellen P₁ und P₂ bedeuten, so kann diese Größe aus den Streifen gleicher Farbordnung wie folgt erschlossen werden:

mit a=(ϕ₁-ϕ₂)/π und b=(ϕ₁-ϕ

)π. Dabei bezeichnen

und

die Wellenlängen maximaler Intensität an den Stellen P

bzw. P

des Eintrittsspaltes, auf welche die oben genannten Punkte P₁ und P₂ abgebildet werden, und ϕ₁, ϕ

, ϕ₂ die Phasensprünge bei den Wellenlängen

. Wenn die reflektierenden Beläge auf den Fizeau-Platten (Abb. 1) aus Silber bestehen, sind a und b vernachlässigbar klein. Da sich Wellenlängen sehr genau messen lassen, kann man auf die geschilderte Weise (mit Vielstrahlinterferenzen) Oberflächenprofile mit Genauigkeiten im nm-Bereich ausmessen. Für den Fall einer planparallelen Platte mit dem Brechungsindex n und der Dicke d sind die M. S. Gerade, die parallel zum Eintrittsspalte verlaufen. Diese Streifen werden manchmal Edser-Butler-Streifen genannt. Ihr Abstand, gemessen in spektroskopischen Wellenzahlen σ₀=1/λ₀, beträgt 1/(2nd), ist also stets der gleiche. Wegen dieser Eigenschaft können sie zur Kalibrierung von Spektrographen verwendet werden. Da sich Wellenlängen sehr genau messen lassen, kann man bei der Dickenmessung Genauigkeiten im Bereich von 0,1 nm erzielen.

Müllersche Streifen 1: Anordnung zur Erzeugung von Müllerschen Streifen. O₁, O₂, O₃ Objektive.

Müllersche Streifen 2: Müllersche Streifen, mit einem Michelson-Interferometer und einem Handspektroskop aufgenommen. Als Weißlichtquelle diente eine Xenon-Hochdrucklampe.