Lexikon der Optik: Mueller-Matrix
Mueller-Matrix, eine reelle 4×4-Matrix, die die Änderung der Stokes-Parameter des Lichtes bei Durchgang durch ein optisches System in der Form S=M·S0 beschreibt. Dabei bezeichnet S0 den aus den Stokes-Parametern gebildeten Vierer-Vektor für das einfallende, S den entsprechenden Vektor für das austretende Licht. Die M. M errechnet sich aus der Jones-MatrixT und der Matrix A (Stokes-Parameter) nach der Formel M=A(T×T†)A-1. Da fast immer eine Reihe von Matrixelementen der M. Null ist und speziell zur Bestimmung der Intensität nur der Stokes-Parameter s0 berechnet zu werden braucht, reduziert sich der Rechenaufwand erheblich und ist oft geringer als im Jones-Formalismus (Jones-Matrix).
Die M. lautet für einen idealen Polarisator in der Orientierung α (Winkel zwischen Schwingungs- und x-Richtung)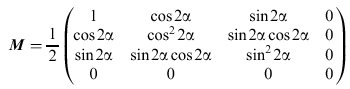
und für eine Oberfläche mit den Reflexionskoeffizienten rx und ry und ellipsometrischen Parametern ψ und Δ (Elipsometrie)
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.