Lexikon der Physik: Fullerene
Fullerene
Siegmar Roth, Stuttgart, und Kun Liu, Shanghai
Fullerene sind fußballartige Kohlenstoffgebilde. Wichtig ist, daß es sich hierbei um graphitartigen Kohlenstoff handelt, während die klassischen Kohlenstoffmodifikationen Diamant ( Abb. 1 ) und Graphit ( Abb. 2 ) sind. Diamant ist vierbindig (›sp3-hybridisiert‹), und jedes Kohlenstoffatom ist von vier nächsten Nachbarn umgeben. Diamant ist somit ein Verwandter des Germaniums und Siliciums, nämlich ein Halbleiter (und zwar ein Halbleiter mit einer so großen Energielücke, ≈ 5 eV, daß er zur Klasse der Isolatoren gehört). Graphit ist schichtartig aufgebaut, die Kohlenstoffatome in einer Schicht sind nur von drei Nachbarn umgeben, der Kohlenstoff ist hier nur dreibindig (›sp2-hybridisiert‹), das vierte Elektron ist über die ganze Schicht ›delokalisiert‹ und steht für eine metallähnliche elektrische Leitfähigkeit zur Verfügung.
In grober Näherung kann man sich die Fulleren-Bälle als Graphitkugeln vorstellen. Das bienenwabenartige Kristallgitter einer Graphit-Schicht besteht aus lauter aneinandergereihten Sechsecken. Wenn sie nur Sechsecke enthält, ist eine Schicht eben, doch wenn man einige Sechsecke durch Fünfecke ersetzt, beginnt sie sich zu wölben. Es stellt sich heraus, daß man 12 Fünfecke braucht, um eine geschlossene Struktur zu erhalten. Der kleinste und regelmäßigste Fulleren-Ball besteht aus 12 Fünfecken und 20 Sechsecken. Er enthält insgesamt 60 Kohlenstoffatome und bildet das Molekül C60. Der Name Fulleren soll an den Architekten Richard Buckminster Fuller erinnern, der ähnliche Polyederkonstruktionen für seine Kuppelbauten verwandte.
Die Struktur des Fulleren-Moleküls C60 ist in Abb. 3 dargestellt. Wegen der Krümmung und wegen der geringen Abmessungen ist Fulleren nicht ganz so metallisch wie Graphit, es ist aber auch nicht so isolierend wie Diamant. Für die Synthese dieses Moleküls erhielten Curl, Kroto und Smalley 1996 den Nobelpreis für Chemie [1].
Ein Fulleren-Herstellungsverfahren besonderer Art ergab sich bei den Bemühungen, Substanzen mit ähnlichen Absorptionslinien zu erzeugen, wie sie in der interstellaren Materie beobachtet werden. Dabei haben Krätschmer und Mitarbeiter die Fulleren-Synthese in der Bogenlampe entwickelt [2], die es erlaubt, mit einfachen Mitteln verhältnismäßig große Mengen von Fulleren zu erzeugen. Das Krätschmer-Verfahren ist in Abb. 4 skizziert. Zwischen zwei Graphitelektroden brennt ein stark rußender elektrischer Entladungsbogen. Eine inerte Atmosphäre schützt den Ruß vor Oxidation. Im Ruß befinden sich neben anderen Kohlenstoffpartikeln verschiedene Fullerene. Diese können mit organischen Lösungsmitteln extrahiert und anschließend chromatographisch getrennt werden.
Ein Molekül aus 60 Atomen ist bereits ein kleiner Festkörper. Genau genommen ist es ein Cluster, ein Gebilde, das zwischen Molekül und Festkörper steht. Man kann im C60-Molekül – da es eine Hohlkugel ist, sollte man vielleicht besser sagen: man kann auf dem C60-Molekül Festkörperphysik betreiben: Man kann Energiebänder berechnen, Energielücken, Exzitonen, Korrelationsenergien u.v.a.m. Man kann aber auch die Moleküle zu einem geordneten Molekülkristall zusammenfügen und so aus lauter Minifestkörpern einen großen Festkörper machen. Ein derartiger Molekülkristall ist in Abb. 5 angedeutet. Natürlich sind die Wechselwirkungen innerhalb der Minifestkörper (die intramolekularen Wechselwirkungen) viel größer als die zwischen den Minifestkörpern (die intermolekularen Wechselwirkungen). Chemisch gesprochen handelt es sich in einem Fall um kovalente Bindungen, im anderen um Van-der-Waals-Bindungen.
Diese unterschiedliche Stärke der Wechselwirkungen führt auch zu unterschiedlichen Energieskalen. Elektronische Energien innerhalb des Minifestkörpers liegen im Bereich von einigen 10 eV, im Molekülkristall betragen sie nur einige Zehntel eV. Das bedeutet, daß die Energiebänder im Molekülkristall sehr schmal sind. Die Minifestkörper sind Halbleiter und auch der Molekülkristall ist ein Halbleiter. Aber den Molekülkristall kann man dotieren, und zwar so stark, daß er zum Metall und sogar zum Supraleiter wird.
Geeignete Dotiermittel sind z.B. die Alkalimetalle. Diese diffundieren in die Lücken zwischen den C60-Molekülen. In der Halbleiter-Terminologie würde man von interstitiellem Dotieren sprechen. Ähnlich wie bei leitenden Polymeren und bei Graphit-Einlagerungsverbindungen wird auch der Ausdruck Interkalieren verwendet. Abb. 6 zeigt die erste Beobachtung der Supraleitung in kaliumdotiertem Fulleren [3]. Man sieht deutlich, wie der elektrische Widerstand beim Abkühlen der Probe bei etwa 12 oder 13 K verschwindet. Inzwischen hat man in Fullerenen bereits supraleitende Sprungtemperaturen von fast 40 K erreicht. Wenn Müller und Bednorz 1986 nicht die Hochtemperatur-Supraleitung in Perowskiten entdeckt hätten, bei denen heute Tc bereits wesentlich über 100 K liegt, hätte man auch für die Supraleitung in Fullerenen einen Nobelpreis vergeben können.
Normalerweise gibt es nur die schwachen Van-der-Waals-Bindungen zwischen den C60-Molekülen im Fulleren-Kristall. Durch besondere Behandlung (Druck, Dotieren, Lichteinstrahlung) kann man Fulleren aber auch polymerisieren. Dann bilden sich kovalente Bindungen zwischen den Molekülen aus [4]. Abb. 7 zeigt eine Fulleren-Kette. Solche Ketten entstehen gelegentlich in alkalidotiertem Fulleren. Sie zeigen dann ähnliche elektrische und magnetische Anomalien wie andere eindimensionale Leiter. So gibt es z.B. Hinweise für Ladungs- und Spindichtewellen.
Da die Fulleren-Bälle Hohlkugeln sind, liegt es nahe, Atome oder Moleküle in den Hohlraum hineinzutun. Man spricht dann von endohedralem Dotieren (endohedrale Fullerene). In C60 kann man vor allem Stickstoff oder Lithium unterbringen, aber bei den höheren Fullerenen gibt es eine ganze Reihe von endohedralen Verbindungen: Sc@C82, La@C82, Y@C82 etc. (Die Schreibweise mit dem Klammeraffen ›@‹ hat sich im Zusammenhang mit endohedralen Verbindungen eingebürgert.) Eines dieser endohedralen Metallofullerene zeigt Abb. 8 .
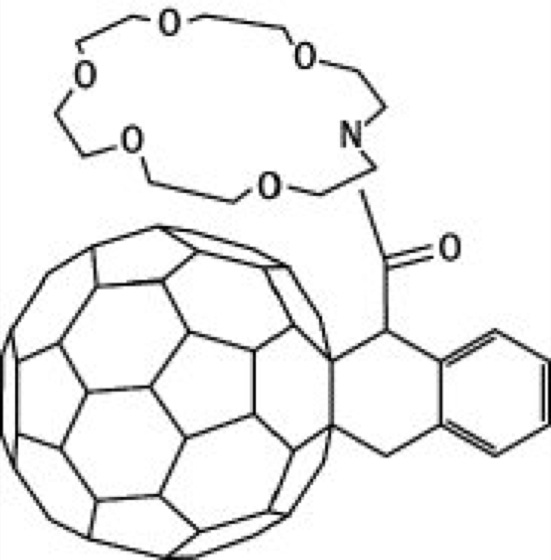
In der organischen Chemie spielt das Benzol eine große Rolle. Benzol ist ein geschlossener Ring aus dreibindigem Kohlenstoff. Es liegt nun nahe, eine analoge Chemie auf Kohlenstoff-Kugeln aufzubauen, etwa indem man eine Bindung auf der Kugel öffnet und daran andere organische Komponenten anhängt. In der Tat gibt es heute bereits eine Vielzahl von Fulleren-Derivaten (die Datenbanken verzeichnen mehr als 10 000 sogenannte Fulleren-Spezies). Als Beispiel eines Fulleren-Derivats ist in Abb. 9 ein Fulleren-Azo-Kronenether gezeigt.
Das Fulleren mit der höchsten Symmetrie ist C60. Aber es gibt zahlreiche größere Fullerene: C70, C82, C84, .... C240, ... Abb. 10 zeigt das eiförmige C70, das nicht wie ein europäischer, sondern eher wie ein amerikanischer Fußball aussieht. Man kann in Gedanken – und auch in der Realität – die Ellipsoide immer länger und länger machen und gelangt so schließlich zu den Kohlenstoff-Nanoröhrchen (Carbon Nanotubes). Diese können bei Durchmessern von nur einigen Nanometern mehrere Mikrometer oder gar Zentimeter lang werden ( Abb. 11 ).
Seit der ersten Synthese sind über 15 000 Einzelveröffentlichungen über Fullerene erschienen, darüber hinaus gibt es zahlreiche Übersichtsarbeiten und Monographien zu diesem Thema. Einen guten Überblick über das Gebiet kann man sich auch durch die Konsultation der Proceedings der Winterschulen in Kirchberg verschaffen [5].
Literatur:
[1] H.W. Kroto, J.R. Heath, S.C. O'Brien, R.F. Curl, R.E. Smalley: Nature 318, 162 (1985).
[2] W. Krätschmer, L.D. Lamb, K. Fostiropoulous, D. Huffmann: Nature 347, 354 (1990).
[3] A.F. Hebard, M.J. Rosseinsky, R.C. Haddon, D.W. Murphy, S.H. Glarum, T.T.M. Palstra, A.P. Ramirez, A.R. Kortan: Nature 350, 600 (1991).
[4] P.W. Stephens, G. Bortel, G. Faigel, M. Tegze, A. Janossy, S. Pekker, G. Oszlanyi, L. Forro: Nature 370, 636 (1994).
[5] Kuzmany, J. Fink, M. Mehring und S. Roth, (Hrsgb.): Electronic Properties of Fullerenes, Springer, Heidelberg 1993.H. Kuzmany, J. Fink, M. Mehring und S. Roth, (Hrsgb.): Progress in Fullerene Research, World Scientific, Singapore 1994.H. Kuzmany, J. Fink, M. Mehring und S. Roth, (Hrsgb.): Physics and Chemistry of Fullerenes and Derivatives, World Scientific, Singapore 1995.
H. Kuzmany, J. Fink, M. Mehring und S. Roth, (Hrsgb.): Fullerenes and Fullerene Nanostructures, World Scientific, Singapore 1996.
H. Kuzmany, J. Fink, M. Mehring und S. Roth, (Hrsgb.): Molecular Nanostructures, World Scientific, Singapore 1998.
![](javascript:ShowPic("/lexika/images/physik/fff4138.jpg", "183", "195");)
Fullerene 1: Kristallstruktur des Diamants. Diamant besteht aus vierbindigem Kohlenstoff und ist ein Halbleiter mit großer Bandlücke (Isolator).
![](javascript:ShowPic("/lexika/images/physik/fff4139.jpg", "188", "161");)
Fullerene 2: Kristallstruktur des Graphits. Die Kohlenstoffatome in den Schichten sind dreibindig, das vierte Elektron der Außenhülle der Kohlenstoffatome steht für metallähnliche Leitfähigkeit entlang der Schicht zur Verfügung.
![](javascript:ShowPic("/lexika/images/physik/fff4140.jpg", "183", "188");)
Fullerene 3: Struktur des Fulleren-Moleküles C60. Das Gebilde ist fast kugelartig mit einem Durchmesser von ungefähr 10 Å (1 Nanometer). Wenn man die Kohlenstoff-Atome durch Kugeln mit dem Van-der-Waals-Radius darstellt, bleibt im Innern ein Hohlraum von etwa 7 Å Durchmesser.
![](javascript:ShowPic("/lexika/images/physik/fff4141.jpg", "321", "269");)
Fullerene 4: Fulleren -Synthese nach Krätschmer: rußender Entladungsbogen zwischen Graphitelektroden.; 1 positive Graphitelektrode, 2 negative Graphitelektrode, 3 Pumpe, 4 Einlaß für Inertgas, 5 Plasmaregion, 6 Kühlwasser ein, 7 Kühlwasser aus, 8 Reaktionskammer, 9 Stromquelle, 10 Reaktionsraum.
![](javascript:ShowPic("/lexika/images/physik/fff4142.jpg", "184", "183");)
Fullerene 5: Anordnung von C60-Molekülen zu einem Molekülkristall.
![](javascript:ShowPic("/lexika/images/physik/fff4143.jpg", "324", "226");)
Fullerene 6: Supraleitung in alkalidotiertem Fulleren [4]. Der spezifische Widerstand ist über der Temperatur aufgetragen.
Fullerene 7: Kette eines Fulleren-Polymers.
![](javascript:ShowPic("/lexika/images/physik/fff4145.jpg", "189", "185");)
Fullerene 8: Endohedrales Metallofulleren.
![](javascript:ShowPic("/lexika/images/physik/fff4146.jpg", "183", "186");)
Fullerene 9: Fulleren-Azo-Kronenether als Beispiel eines der zahlreichen Fullerenderivate.
![](javascript:ShowPic("/lexika/images/physik/fff4147.jpg", "183", "163");)
Fullerene 10: C70, ein Fulleren, das nicht wie ein europäischer, sondern eher wie ein amerikanischer Fußball aussieht.
Fullerene 11: Kohlenstoff-Nanoröhrchen können bei Durchmessern von nur wenigen Nanometern einige Mikrometer oder gar Zentimeter lang werden.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.