Wunschartikel: Informatik: Glücksfall-Algorithmen
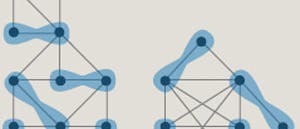
Ein Beispiel möge erläutern, wie diffizil die Unterscheidung zwischen leicht und schwer im Einzelfall ist. Wir betrachten einen mathematischen Graphen, also eine Zusammenstellung von "Ecken" oder "Knoten" (durch Punkte dargestellt) und "Kanten" (Linien, die jeweils zwei Ecken miteinander verbinden).
Gibt es in diesem Graphen einen Weg, der jede Kante genau einmal durchläuft und dann zu seinem Ausgangspunkt zurückkehrt? Für jeden Graphen mit endlich vielen Kanten könnten wir diese Frage mit brute force ("roher Gewalt") beantworten: Wir probieren alle möglichen Wege der Reihe nach durch, ob sie die Bedingungen erfüllen. Es gibt aber ein erheblich besseres Verfahren: Leonhard Euler (1707 – 1783) bewies 1736, dass es einen solchen Weg (der heute "Euler-Kreis" heißt) genau dann gibt, wenn in jeder Ecke eine gerade Anzahl von Kanten zusammentrifft. Das ist leicht zu überprüfen und erspart einem die überaus mühsame erschöpfende Suche.
Nehmen wir jetzt denselben Graphen, stellen aber wie William Rowan Hamilton (1805 – 1865) eine etwas andere Frage: Gibt es einen Weg, der jede Ecke genau einmal durchläuft (einen "Hamilton-Kreis")? Diesmal gibt es keine Alternative zur rohen Gewalt. Bis heute kennt niemand eine Methode, die für jeden Graphen die richtige Antwort liefert und deutlich schneller arbeitet als die erschöpfende Suche.
Die beiden so ähnlich aussehenden Probleme sind so unterschiedlich schwierig wie nur denkbar. Woran liegt das? Gibt es einfach keine kurze Lösung für das Hamilton-Problem, oder sind wir bisher nur zu beschränkt, um sie zu finden? Die meisten Wissenschaftler sind von Ersterem überzeugt – aber bewiesen ist noch nichts. Und schließlich könnten jederzeit völlig neue, überraschende Ideen zur Lösung solcher Probleme auftauchen. Vor 1736 sah die Frage nach der Existenz eines Euler-Kreises schließlich auch schwer aus...








Schreiben Sie uns!
Beitrag schreiben