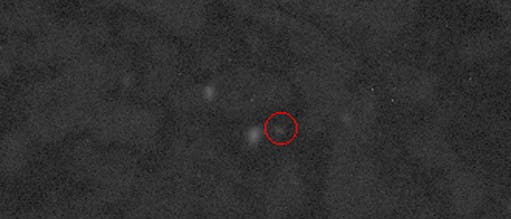
Erdnahe Objekte sind Asteroiden, die um die Sonne kreisen und dabei die Erdumlaufbahn kreuzen. Käme es an diesem Schnittpunkt auch zu einem zeitlichen Zusammentreffen, würde der Brocken unweigerlich mit der Erde kollidieren. Viele erdnahe Objekte (Near Earth Objects, NEOs) und ihre Bahnen sind bereits bekannt, so dass man bei einem möglichen Zusammenstoß vorgewarnt wäre. Wenn dann noch genügend Zeit bleibt, würde es reichen, mit einem Raumschiff beispielsweise über die Massenanziehung die Asteroidenbahn minimal zu verändern. Doch kennt man heute bei Weitem noch nicht alle NEOs. Um noch mehr dieser Risikoobjekte zu erfassen und ihre Bahnen zu kartieren, hat Morgan Rehnberg ein spezielles Computerprogramm entwickelt. Auf der Suche nach bedrohlichen Asteroiden vergleicht es automatisch viele Bilder des Sternhimmels.

Am National Optical Astronomy Observatory (NOAO) läuft unter der Leitung von Mark Trueblood ein Programm, das NEOs auffinden soll. Da den Astronomen jedoch bis vor Kurzem eine geeignete Software fehlte, erhielt im vergangenen Sommer der Student Rehnberg den Auftrag, eine solche zu erstellen. Sein Computerprogramm PhAst (eine Abkürzung von Photometry-Astrometry) kann digitale Aufnahmen eines Teleskops in rascher Folge analysieren. Denn Asteroiden bewegen sich schnell über den Himmel hinweg – dabei lässt sich ihre Bahn verfolgen. Blinkt dabei ein Asteroid auf den Fotos auf, so ordnet Rehnbergs Softwarekode ihm mit Rektaszension und Deklination sofort die Koordinaten am Himmel zu.

Rehnberg kam im Rahmen von Research Experience for Undergraduates (REU) an seinen außergewöhnlichen Sommerjob. REU erlaubt Studenten im Grundstudium Einblicke in die astronomische Forschung. Rehnbergs PhAst-Code hat sich mittlerweile bewährt: Im Oktober wurde damit auf Bildern des Teleskops am Kitt Peak National Observatory der erdnahe Asteroid NEO2008 QT3 gesichtet. Gegenüber der Vorläufersoftware konnte PhAst die Größe der Fehlerbalken beim Bestimmen der Helligkeit und der Position des Objekts halbieren.

Laura Hennemann