Achtpunktekreis
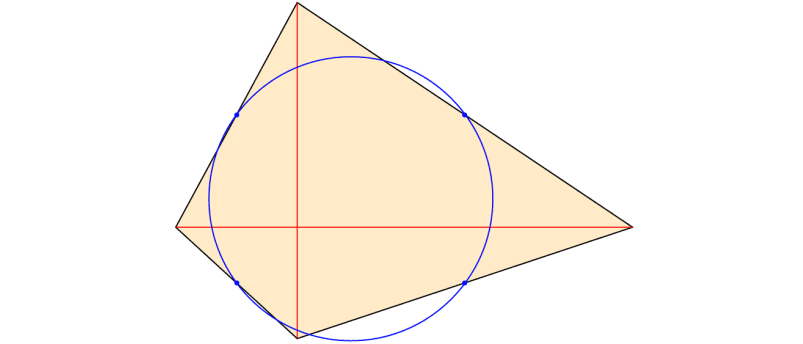
Zeigen Sie bitte, dass die Seitenmitten eines Vierecks mit zueinander rechtwinkligen Diagonalen auf einem Kreis liegen.
Was für ein Viereck bilden die Seitenmitten?
Nach dem Satz von Varignon ist das Viereck aus den Seitenmitten eines (beliebigen!) Vierecks ein Parallelogramm. Dessen Seiten sind parallel zu den Diagonalen des ursprünglichen Vierecks. Also ist unser spezielles Varignon-Parallelogramm ein Rechteck.
Ein Rechteck hat bekanntlich einen Umkreis.
Aber der Kreis soll ja "Achtpunktekreis" heißen. Was ist mit dessen anderen Schnittpunkten mit den Viereckseiten? Denken Sie an den Thaleskreis.
Die anderen vier Schnittpunkte sind die Fußpunkte der Lote von den Seitenmitten auf die jeweilige Gegenseite (oder deren Verlängerung).
Dieser Satz über den Achtpunktekreis ermöglicht einen sehr eleganten Beweis des Satzes vom Neunpunktekreis. Dieser sagt, dass es für ein Dreieck einen Kreis gibt, der durch die Seitenmitten, die Höhenfußpunkte und die (nach Euler benannten) Halbierungspunkte zwischen den Ecken und dem Höhenschnittpunkt geht.
Die Ecken eines beliebigen Dreiecks und sein Höhenschnittpunkt sind die Ecken von drei verschiedenen Vierecken, deren Diagonalen sämtlich rechtwinklig zueinander liegen.
In jedem der drei Vierecke fallen die Fußpunkte der Lote von den Mitten der Gegenseiten (blau) paarweise zusammen. Zusammen mit den vier Seitenmitten liefert jedes der drei Vierecke sechs spezielle Punkte auf dem gemeinsamen Kreis. Wie zu sehen ist, sind es aber trotzdem nur insgesamt 9 verschiedene. Bezogen auf das Dreieck sind das die drei Seitenmitten, die drei Euler-Punkte und die drei Höhenfußpunkte. Das Dreieck hat somit einen Neunpunktekreis.
Kann man nun auch den Satz von Beltrami besonders einfach beweisen? Dieser sagt, dass der Schwerpunkt der drei Ecken und des Höhenschnittpunktes eines Dreiecks der Mittelpunkt des Neunpunktekreises ist.
Wir sehen uns noch einmal das Bild an:
Der gesuchte Punkt ist Schwerpunkt eines (beliebigen) der drei genannten Vierecke. Wie fassen dessen vier Ecken zu zwei Paaren zusammen und bestimmen den Schwerpunkt jedes Paars. Diese beiden Schwerpunkte liegen auf dem Achtpunktekreis einander genau gegenüber, sind also Enden eines Durchmessers. Auf diesem Durchmesser muss der Schwerpunkt des gesamten Vierecks liegen. Dasselbe gilt, wenn man die Ecken des Vierecks auf die andere Weise zu Paaren zusammenfasst. Also muss der Schwerpunkt ium Schnittpunkt der Durchmesser, sprich im Mittelpunkt des Kreises liegen.
Der Neunpunktekreis des Dreiecks wurde 1821 von Poncelet gefunden (ein Jahr später auch von Feuerbach, der auch dessen Berührpunkt mit dem Inkreis entdeckt hat: Satz von Feuerbach).
Man könnte nun meinen, dass der Achtpunktekreis so einfach zu finden ist, dass es für die Antike kein Problem hätte sein sollen. Tatsächlich wurde er erst 1944 von Louis Brand in Cincinnati entdeckt.
Schreiben Sie uns!
Beitrag schreiben