Ameisen-Geometrie auf der Vase

Eine mathematisch gebildete Ameise geht auf einer Vase, über deren Gestalt noch zu reden sein wird, spazieren. Besonders gerne geht sie auf geschlossenen Wegen mit drei plötzlichen Richtungsänderungen nach links und dazwischen Stücken, die so gerade sind, wie es auf dieser Oberfläche überhaupt geht, d.h. sie wandert um Dreiecke.
Nun stellt sie fest, dass es auf dieser Vase genau zwei Sorten von Dreiecken gibt: solche mit der Winkelsumme 180o und solche mit 240o.
Welche Gestalt hat die Vase?
Die Oberfläche der Vase ist Teil eines Kegelmantels. Wenn man diese Mantelfläche entlang einer Mantellinie aufschneidet und in eine Ebene abwickelt, bilden die beiden jetzt getrennten Schnittlinien einen Winkel von 60o, allgemein den Winkel \( \varepsilon \), um den die Winkelsumme in einem Teil der Dreiecke auf dem Kegel größer ist als bei den anderen und in der Ebene.
Die beiden Sorten der Dreiecke auf dem Kegel unterscheiden sich dadurch, dass sie die Spitze \(P\) des Kegels umschließen (gelb) oder auch nicht (grün). Anders gesagt: Bei der ersten Sorte kann man die Mantelfläche aufschneiden, ohne dabei das Dreieck zu treffen. Das Dreieck wird beim Abwickeln in die Ebene zu einem gewöhnlichen (ebenen) Dreieck und hat daher auch die vertraute Winkelsumme.
Die abgewickelte Mantelfläche kann so aussehen:
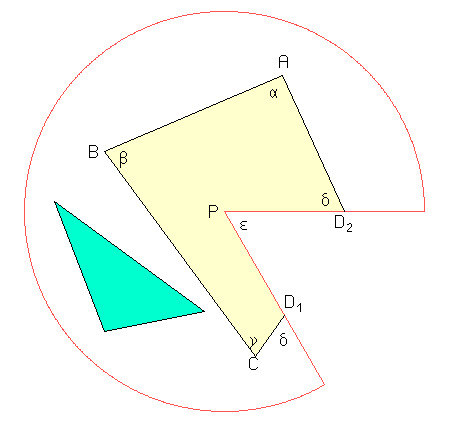
Die Punkte \(D_1\) und \(D_2\) fallen auf dem Kegel zusammen. Sie bilden den Schnittpunkt der Dreiecksseite \(AC\) mit der schneidenden Mantellinie. Entgegen dem ersten Anschein knickt die Wanderroute an dieser Stelle nicht ab; vielmehr bildet sie diesseits wie jenseits der Schnittlinie mit dieser den Winkel \(\delta\). Aus der Winkelsumme \( 4\pi \) im Sechseck \(PD_2ABCD_1\) ergibt sich \( \alpha + \beta + \gamma = \pi + \varepsilon \).
Versäumen Sie es auch nicht, die Figur auf Papier zu zeichnen, auszuschneiden und zu einem Kegelmantel zusammenzurollen.



Schreiben Sie uns!
Beitrag schreiben