Das Zerschneiden geht so:

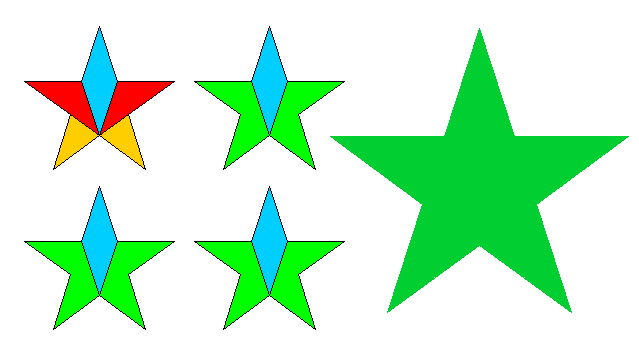
Jetzt müssen Sie nur noch puzzeln.

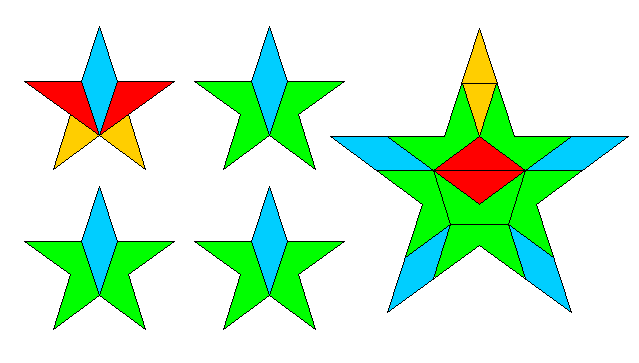
In den Teilstücken erkennt man die Bauteile wieder, die einem bei Mustern auf Basis des regelmäßigen Fünfecks so gut wie zwangsläufig unterkommen: die beiden "goldenen Dreiecke" (gleichschenklige Dreiecke mit dem Seitenverhältnis des goldenen Schnitts), die für die nichtperiodischen Penrose-Pflasterungen eine entscheidende Rolle spielen (siehe auch hier oder in dem "Spektrum"-Sonderheft "Lustvolle Geometrie"); die Raute, die aus zwei schmalen goldenen Dreiecken zusammengesetzt ist, und "Mukundis Krone", das Fünfeck mit der einspringenden Ecke, das die Ebene sowohl periodisch als auch nichtperiodisch auf vielerlei Weisen pflastert.

Man muss übrigens die Pentagramme nicht wie im Tipp angegeben zerschneiden. Roland Schröder hat eine etwas raffiniertere Zerlegung gefunden, die sogar mit 13 Teilen auskommt: