1894 gründete der amerikanische Mathematiker Benjamin Finkel die Zeitschrift »American Mathematical Monthly«, die sich an Mathematikstudenten und Mathematiklehrer wendet, aber auch an Mathematiker, die in der Forschung arbeiten. Vom ersten Heft an enthielt die Zeitschrift eine Kolumne mit dem Titel »Problems and Solutions«, in der Leser mathematische Knobeleien stellen und lösen. Bis heute sind etwa 12 000 Probleme publiziert worden. 1971 stellte Jordi Dou aus Barcelona in Spanien in der Kolumne folgende Aufgabe:

219 rote und 181 grüne Punkte sind zu einem quadratischen Raster von 20×20 Punkten angeordnet. Liegen zwei Punkte in derselben Zeile oder Spalte direkt nebeneinander, sind sie durch eine gerade Linie miteinander verbunden. Sind beide Punkte rot, ist auch die Linie rot, sind beide Punkte grün, ist auch die Linie grün, sind hingegen die Punkte verschiedenfarbig, ist die Linie schwarz. 39 der roten Punkte liegen auf dem Rand des Rasters, allerdings keiner auf einer Ecke, und 237 Verbindungslinien sind schwarz. Wie viele grüne Verbindungslinien gibt es?

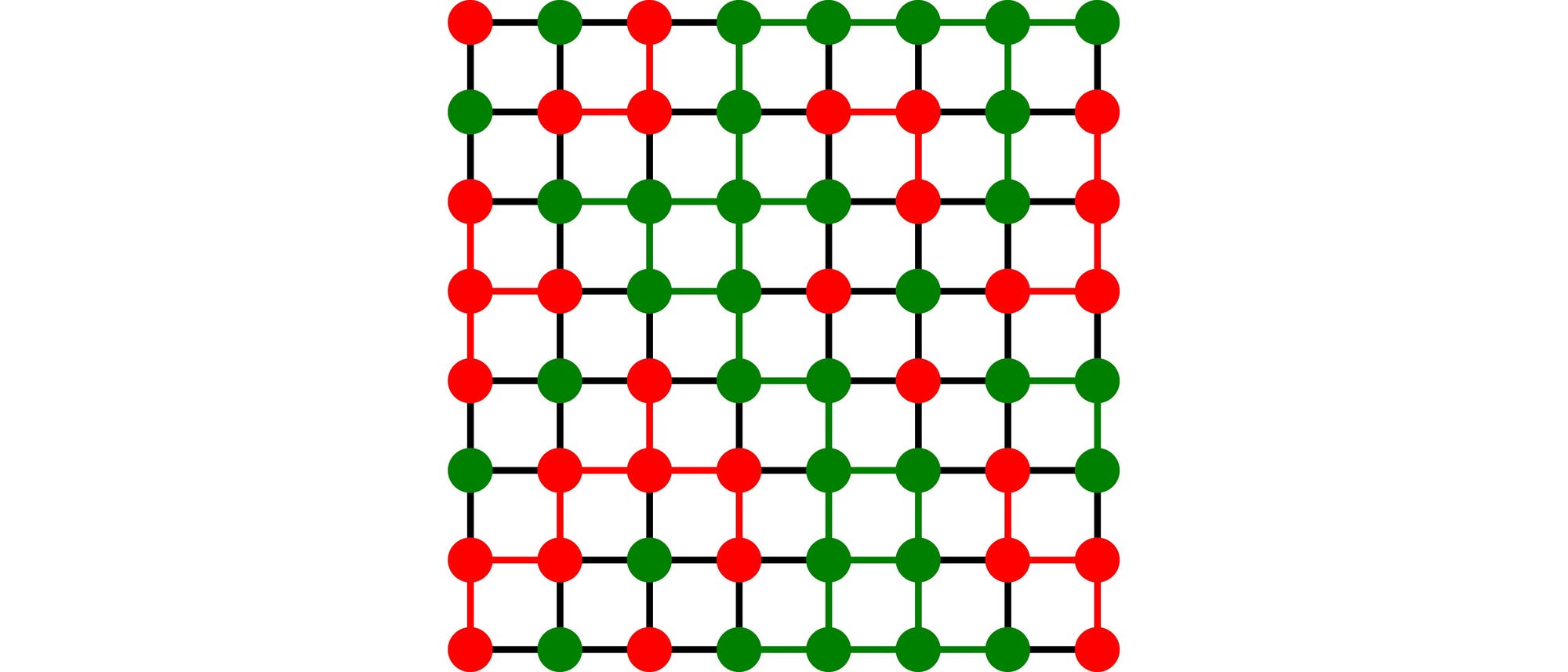
Die Zeichnung zeigt als Beispiel ein Raster von 8×8 farbigen Punkten und den korrekten roten, grünen und schwarzen Verbindungslinien, das aber natürlich nicht die Lösung ist.