Hemmes mathematische Rätsel: Das geteilte Dreieck
Manfred Pietsch vom Stiftischen Gymnasium in Düren in Nordrhein-Westfalen hat 2018 eine Knobelei aus der elementaren Geometrie erdacht.
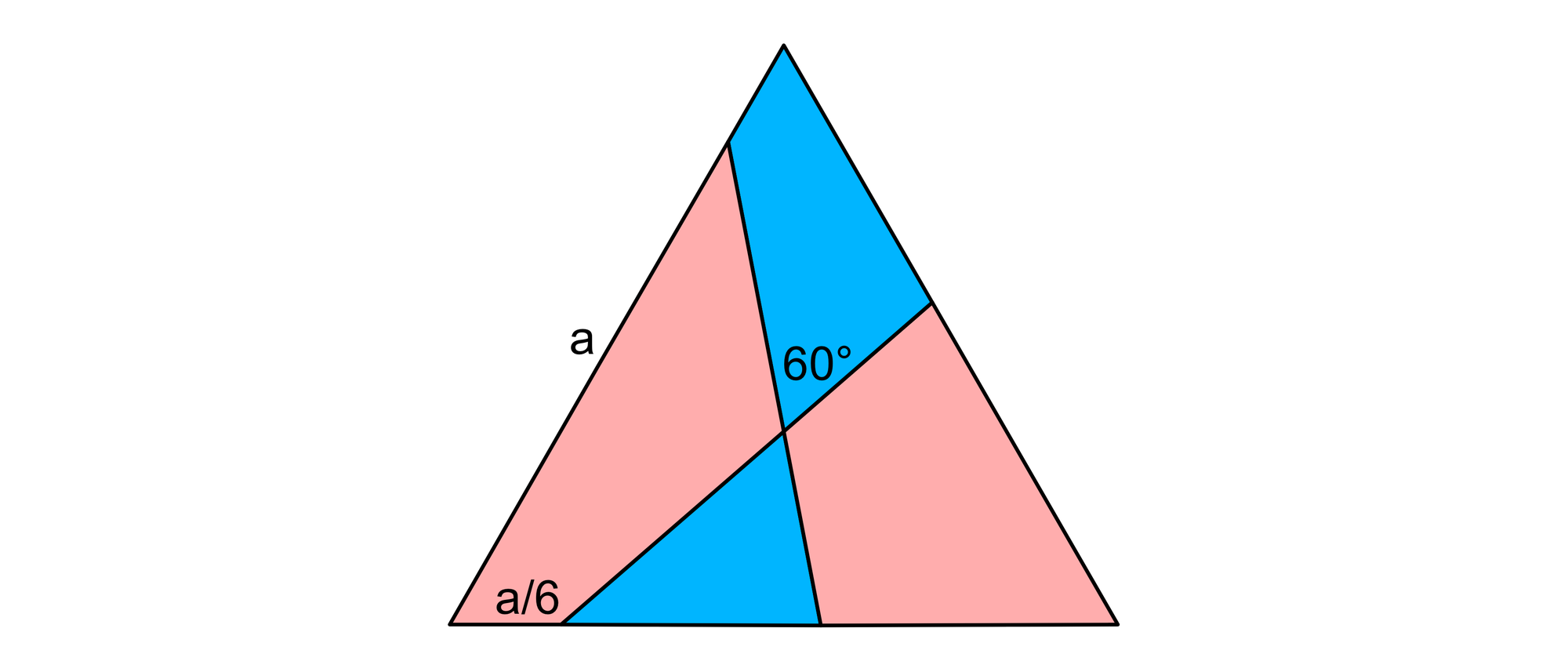
Durch ein gleichseitiges Dreieck wird eine gerade Linie gezogen. Sie beginnt an der unteren Seite des Dreiecks in einem Abstand von a/6 von der linke Ecke, läuft durch den Mittelpunkt des Dreiecks und endet an der rechten Seite des Dreiecks. Eine zweite gerade Linie verbindet die untere Seite des Dreiecks mit seiner linken und läuft auch durch den Mittelpunkt des Dreiecks. Die beiden Linien schneiden sich unter einem Winkel von 60° und zerlegen das Dreieck in vier Teile, die so gefärbt werden, wie es die Skizze zeigt. In welchem Verhältnis steht der Gesamtinhalt der beiden roten Flächen zum Gesamtinhalt der beiden blauen Flächen?
Da die beiden Winkel der blauen Flächen, die sich am Dreiecksmittelpunkt treffen, α = 60° groß sind, müssen die beiden anderen Winkel je eine Größe von 120° haben. Halbiert man sie durch eine Strecke, die die linke und die rechte Seite des Dreiecks verbindet, stoßen sechs 60°-Winkel in Dreiecksmittelpunkt aneinander, und die Figur zerfällt in drei unregelmäßige Dreiecke und drei unregelmäßige Vierecke.
Wegen der Symmetrie sind sowohl diese Dreiecke als auch die Vierecke deckungsgleich. Folglich sind die beiden hellroten und die beiden dunkelroten Flächen zusammen doppelt so groß wie die beiden blauen Flächen. An welchen Stellen die Strecken auf die Dreiecksseiten stoßen, spielt dabei übrigens keine Rolle.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.