Hemmes mathematische Rätsel: Die Schlange auf dem Schachbrett
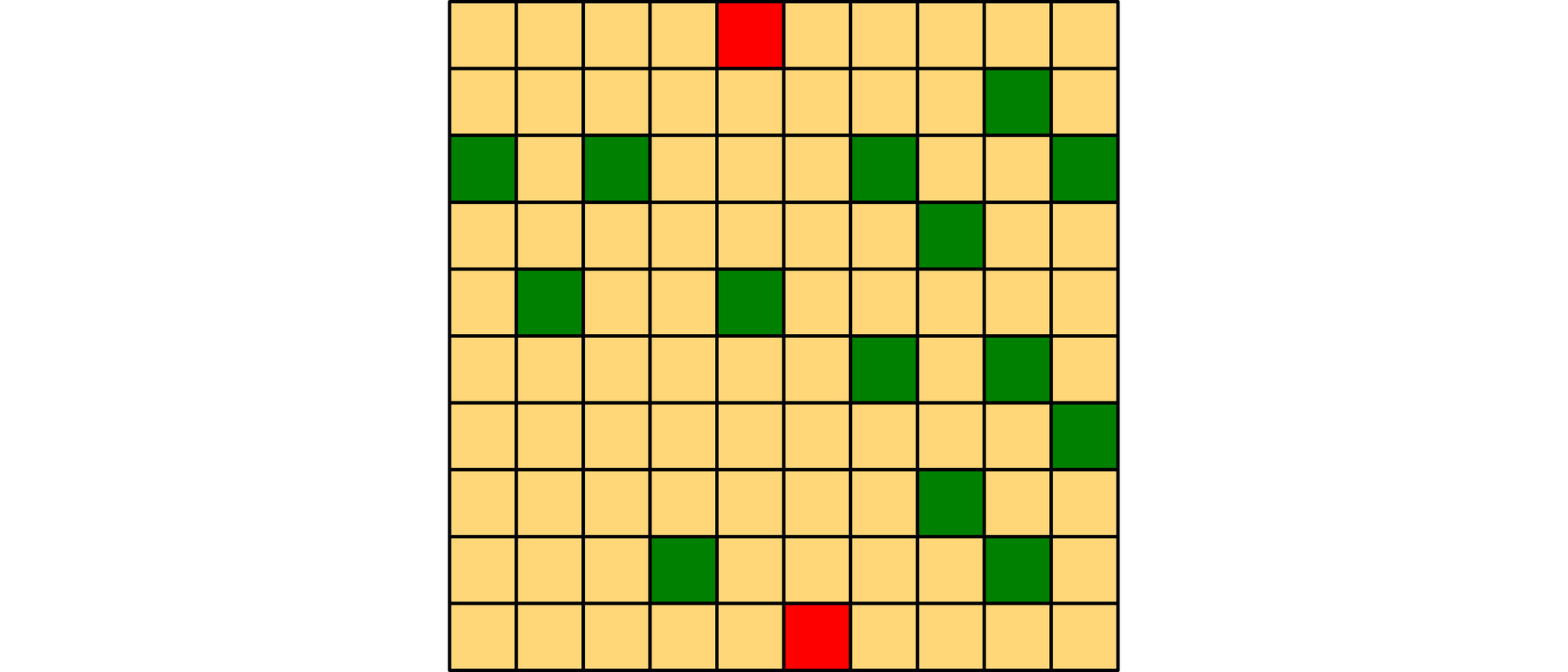
Seit dem Jahr 2000 wird jährlich in der ungarischen Hauptstadt Budapest die »24 Hours Puzzle Championship« ausgetragen. Eine der Aufgaben der vierten Meisterschaft, die am 24. und 25. Mai 2003 stattfand, war das Schlangenrätsel von László G. Nagy.
Die Teilnehmer mussten dabei eine Schlange in ein 10x10-feldiges Schachbrett zeichnen. Diese Schlange sollte aus genau 45 mit den Seiten aneinanderhängenden Feldern bestehen. Der Kopf und die Schwanzspitze der Schlange waren die beiden roten Felder in der obersten und der untersten Reihe. Die Schlange durfte sich nicht schneiden oder selbst berühren, nicht einmal mit Feldecken. Alle grünen Felder waren Teile des Schlangenkörpers. Wie lag die Schlange auf dem Brett?
Die Verbindung der roten und grünen Felder des Bretts zu einer Schlange, die sich nicht selbst schneidet oder berührt, ist fast überall sofort eindeutig. Nur zwischen den beiden linken grünen Feldern in der dritten Reihe gibt es drei verschiedene Möglichkeiten, aber nur eine davon führt zu eine Schlangenlänge von genau 45 Feldern.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.