Hemmes mathematische Rätsel: Das gevierteilte Dreieck
Math Horizons ist eine vierteljährlich erscheinende Zeitschrift, die von der Mathematical Association of America herausgegeben wird. Sie wendet sich an mathematisch interessierte Schüler, Studenten, Lehrer und Laien und bringt Artikel, in den es weniger um die mathematische Forschung und mehr um die mathematische Kultur geht. Die Zeitschrift hat auch eine Denksportecke, aus der das heutige Rätsel entnommen ist. Die Aufgabe stammt von V. Proizvolov und wurde im Frühjahr 1994 veröffentlicht.
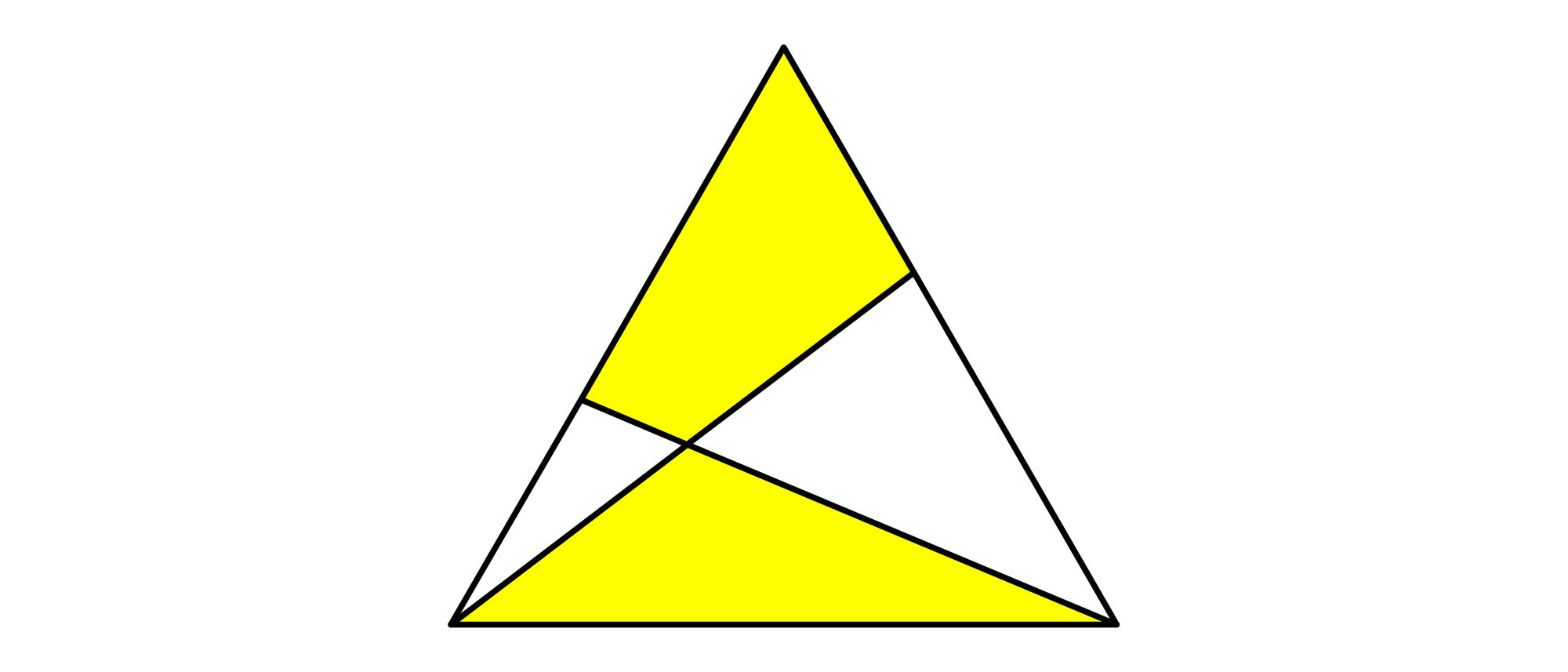
In ein gleichseitiges Dreieck sind zwei Strecken gezeichnet worden, die die linke untere Ecke mit der rechten Seite und die rechte untere Ecke mit der linken Seite verbinden. Die beiden dadurch entstandenen gelben Flächen sind gleich groß. Unter welchen Winkeln schneiden sich die Verbindungsstrecken?
Da die beiden gelben Flächen A und D gleich groß sind, hat auch das Dreieck, das sich aus A und B zusammensetzt, den gleichen Flächeninhalt wie das Dreieck aus B und D. Beide Dreiecke haben je eine Seite, die so lang ist wie die Seiten des äußeren gleichseitigen Dreiecks und am linken Ende dieser Seite einen 60-Grad-Winkel. Da auch ihre Flächeninhalte gleich groß sind, müssen die beiden Dreiecke AB und BD deckungsgleich sein.
Dreht man nun das gleichseitige Dreieck samt der beiden Verbindungslinien um seinen Mittelpunkt im Uhrzeigersinn um 120 Grad, fällt es wieder mit sich selbst zusammen und die Verbindungslinie b liegt anschließend dort, wo vorher die Linie a gelegen hat. Folglich schließen die Verbindungslinien stumpfe Winkel von 120 Grad und spitze Winkel von 60 Grad ein.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.