Hemmes mathematische Rätsel: Das gevierteilte Dreieck
Nobuyuki Yoshigahara war Japans bedeutendster Puzzle- und Rätselerfinder. Er wurde am 27. Mai 1936 geboren und arbeitete zunächst als Chemiker und später, nach einem Laborunfall, als Mathematiklehrer. Er verfasste mehr als 70 Bücher über Denksportaufgaben und schrieb zahlreiche Rätselkolumnen. Yoshigahara erfand zahlreiche mechanische Puzzle, von denen viele auch von Spielzeugherstellern produziert und vertrieben werden. Er war einer der Begründer der »International Puzzle Party«, bei der sich einmal jährlich die Puzzleexperten der Welt treffen. Yoshigahara starb am 19. Juni 2004.
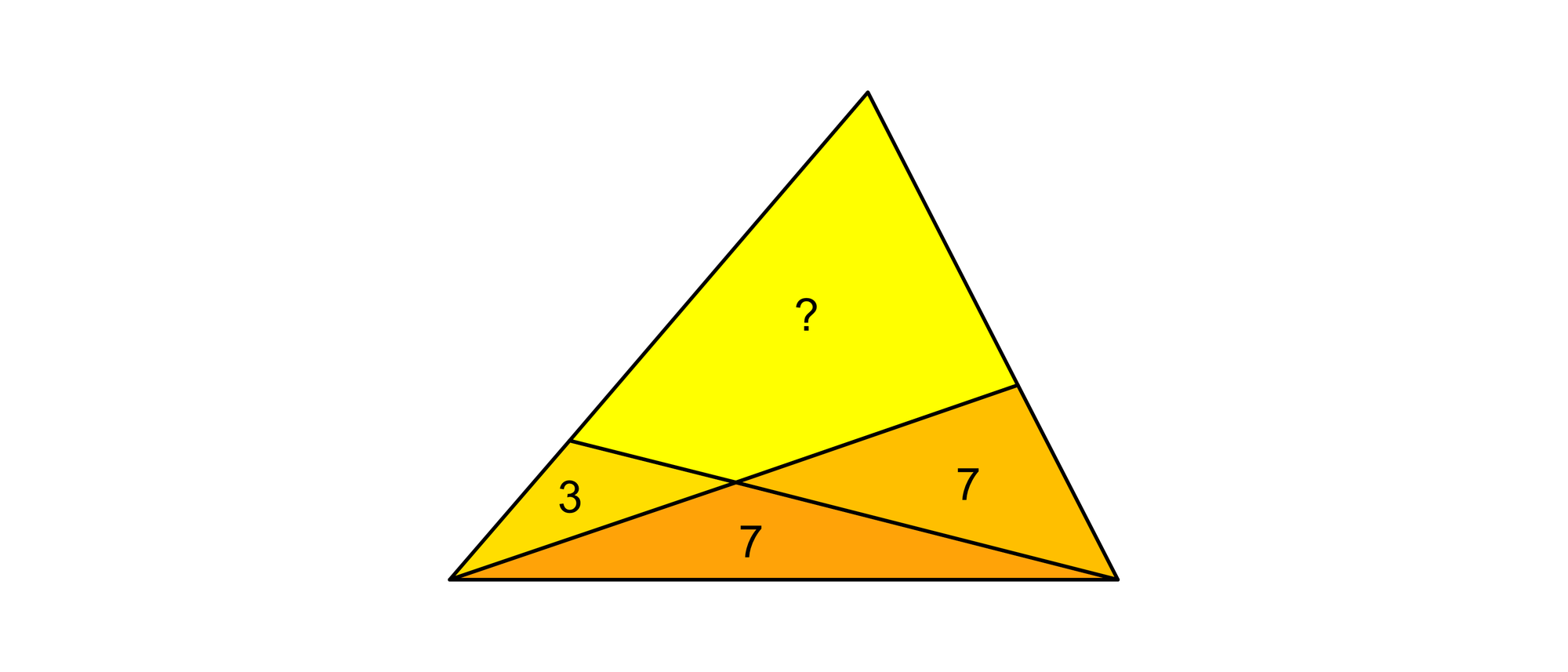
Aus seinem 2002 erschienenen Buch »Chocho Nanmon Suri Pazuru« stammt folgendes Problem: Ein unregelmäßiges Dreieck ist durch zwei Strecken, die zwei Ecken mit den jeweils gegenüberliegenden Seiten verbinden, in drei Dreiecke und ein Viereck unterteilt worden. Die Flächeninhalte der Dreiecke sind 3, 7 und 7. Wie groß ist der Flächeninhalt des Vierecks?
Bevor wir die eigentliche Aufgabe lösen, betrachten wir zunächst folgende Figur.
Die beiden kleinen Dreiecke mit den Flächen A und B haben die Grundseiten a und b und die gemeinsame Höhe h. Ihre Inhalte betragen somit A = 1⁄2ah und B = 1⁄2bh. Auch die beiden großen Dreiecke mit den Flächen A + C und B + D haben die Grundseiten a und b. Ihre gemeinsame Höhe ist k. Folglich betragen ihre Inhalte A + C = 1⁄2ak und B + D = 1⁄2bk. Daraus ergibt sich für die Flächenverhältnisse (A + C)/A = k/h und (B + D)/B = k/h. Diese beiden Flächenverhältnisse sind also gleich: (A + C)/A = (B + D)/B. Damit gilt auch A/A + C/A = B/B + D/B und C/A = D/B.
Dies wenden wir jetzt auf unser eigentliches Problem an.
Mit einer zusätzlichen Linie teilen wir das Viereck in zwei Dreiecke, die die Flächeninhalte A und B haben. Jetzt gilt A/(B + 7) = 3/7 und B/(A + 3) = 7/7. Löst man die zweite Gleichung nach B auf, erhält man B = A + 3. Dies setzt man in die erste Gleichung für B ein. Dadurch bekommt man A/(A + 3 + 7) = 3/7, was sich zu A = 71⁄2 vereinfachen lässt. Mit diesem Wert für A ergibt sich B = 101⁄2. Das Viereck hat somit eine Fläche von A + B = 18.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.