Hemmes mathematische Rätsel: Der König auf dem Schachbrettchen
Beim schriftlichen Abitur im Leistungsfach Mathematik wurde am 23. April 2010 in Thüringen eine Schachaufgabe gestellt.
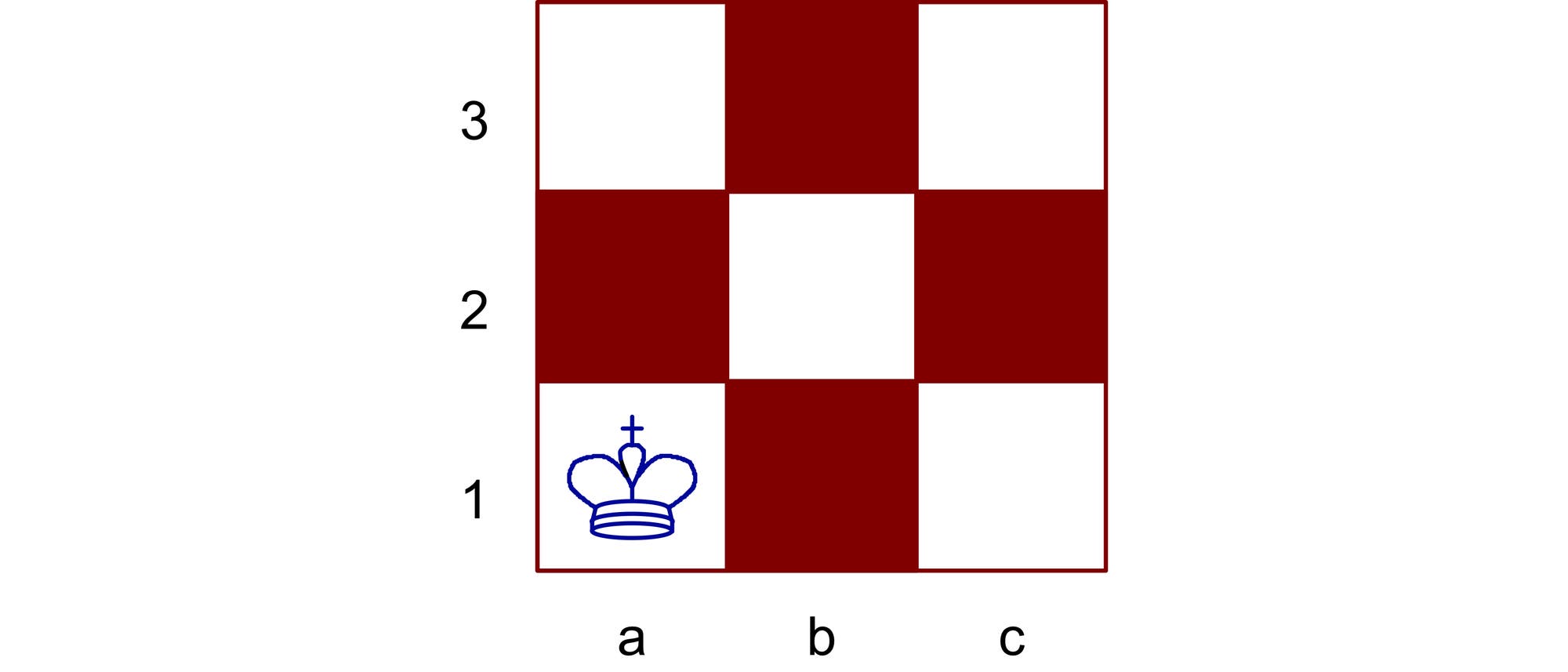
Auf einem kleinen Schachbrett, das nur 3×3 Felder hat, steht als einzige Figur ein König auf dem Feld A1. Wie groß ist die Wahrscheinlichkeit, dass der König nach seinem zweiten Zug auf dem Feld A3 steht, wenn alle erlaubten Züge gleich wahrscheinlich sind?
Mit seinem ersten Zug erreicht der König jeweils einer Wahrscheinlichkeit von 1⁄3 eines der drei Felder A2, B1 und B2. Vom Feld A2 aus kann er fünf verschiedene Felder erreichen, von denen eines das Feld A3 ist. Die Wahrscheinlichkeit von A2 aus A3 zu erreichen ist somit 1⁄5.
Steht der König auf dem Feld B2, kann er auf acht Felder, darunter auch auf A3, ziehen. Die Wahrscheinlichkeit von dort aus A3 zu erreichen, ist also 1⁄8.
Von B1 aus kann der König das Feld A3 mit einem Zug gar nicht erreichen.
Somit beträgt die Wahrscheinlichkeit, dass der König vom Feld A1 aus das Feld A3 in zwei Zügen erreicht 1⁄3 · (1⁄5 + 1⁄8 + 0) = 13⁄120 ≈ 10,83 Prozent.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.