Hemmes mathematische Rätsel: Das Huckepackquadrat
Der »National Council of Teachers of Mathematics«, ein Verband amerikanischer Mathematiklehrer, gibt seit über 100 Jahren monatlich die Zeitschrift »The Mathematics Teacher« heraus. Das mittlere Doppelblatt jedes Heftes lässt sich herausnehmen und ist ein Kalender des jeweiligen Monats, der für jeden Tag eine mathematische Denksportaufgabe enthält. Die Aufgaben werden von Lehrern und Schülern zusammengestellt. Ein paar Hundert dieser Kalenderprobleme sind inzwischen zu zwei Büchern zusammengestellt worden. Das heutige Rätsel ist das Rätsel vom 5. Januar 1990 und stammt von Larry Hoehn von der Austin Peay State University in Tennessee.
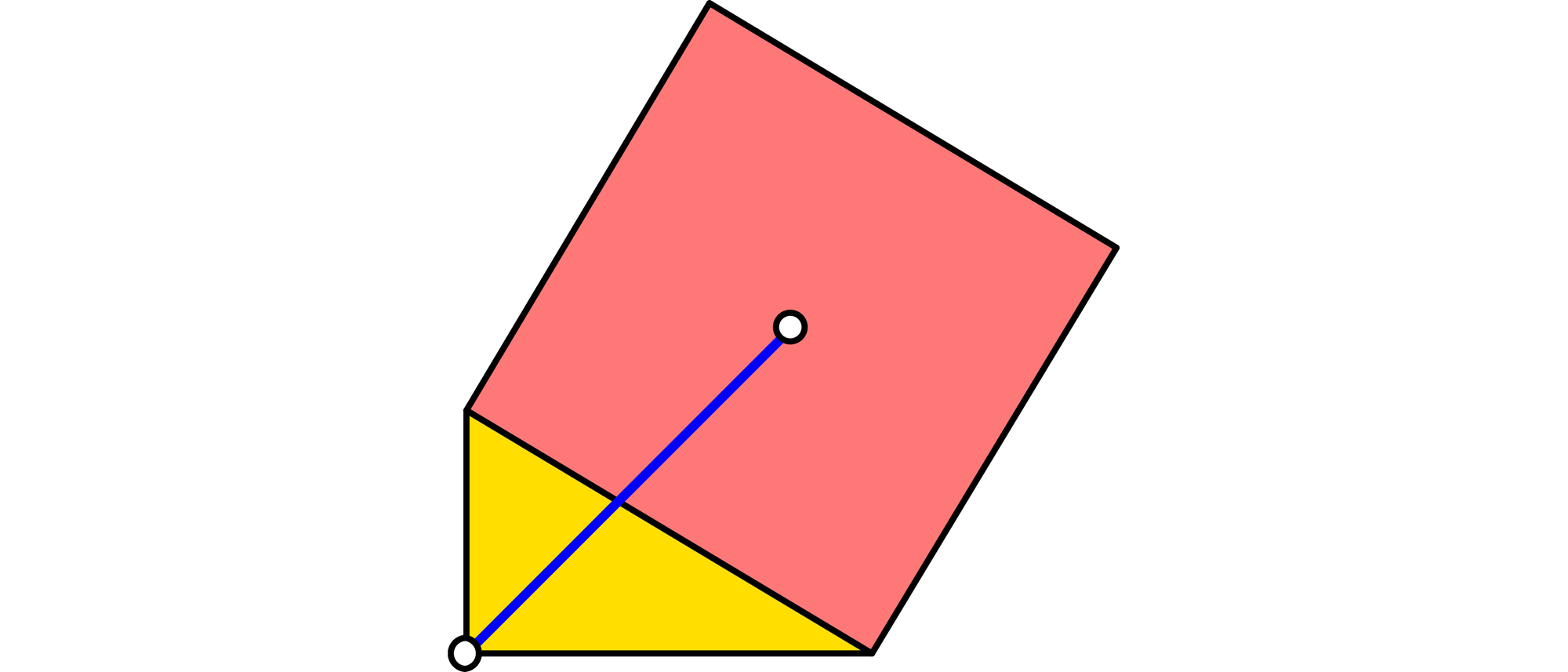
Ein beliebiges rechtwinkliges Dreieck trägt huckepack auf seiner Hypotenuse ein Quadrat. Die Ecke am rechten Winkel des Dreiecks und der Mittelpunkt des Quadrats sind durch eine Strecke miteinander verbunden. Welche Winkel in Abhängigkeit vom Kathetenlängenverhältnis schließen die beiden Katheten mit dieser Strecke ein?
Zeichnet man auf die drei noch freien Seiten des Quadrats deckungsgleiche Kopien des ursprünglichen rechtwinkligen Dreiecks, bilden die acht Katheten ein Quadrat und die Verbindungsstrecken zum Mittelpunkt des Huckepackquadrates dessen Diagonalen. Und da die Diagonalen eines Quadrates mit den Seiten Winkel von 45 Grad einschließen, haben auch die Winkel zwischen der Verbindungsstrecke und den Katheten eine Größe von 45 Grad. Das Kathetenverhältnis spielt dabei keinerlei Rolle.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.