Das innere Dreieck

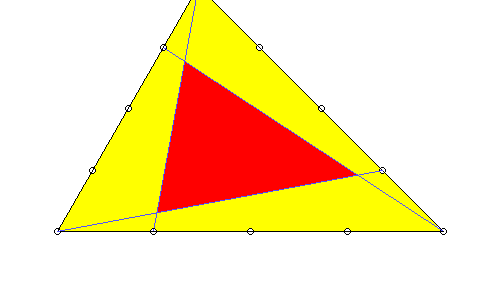
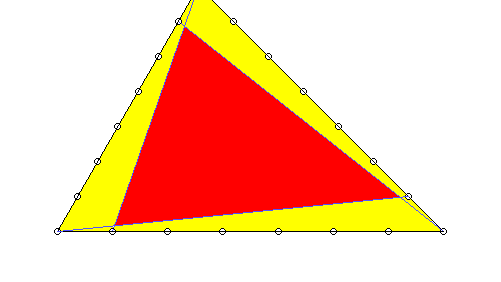
Jede Ecke eines Dreiecks wird mit dem Punkt der gegenüberliegenden Seite verbunden, der diese im Verhältnis 1/3 zu 2/3 teilt. Gefragt ist nach dem Verhältnis der innen von diesen Linien begrenzten Fläche zu der des ganzen Dreiecks.
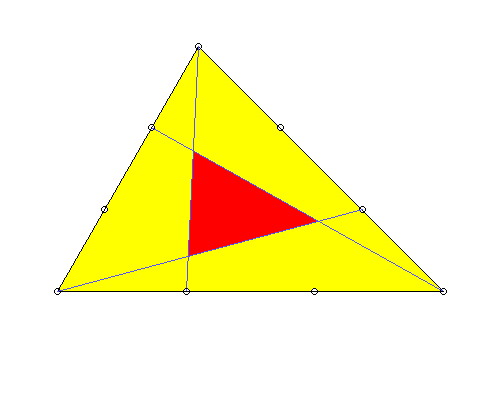
Das Verhältnis ist 1:7. Der Beweis kann unterschiedlich elegant geführt werden, notfalls auch durch Ausrechnen mit Koordinaten.
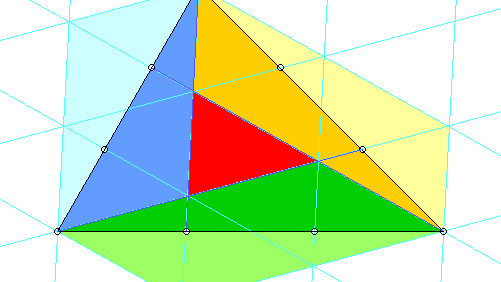
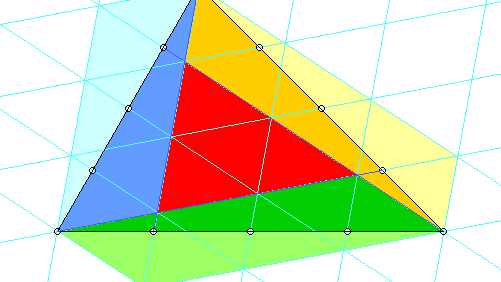
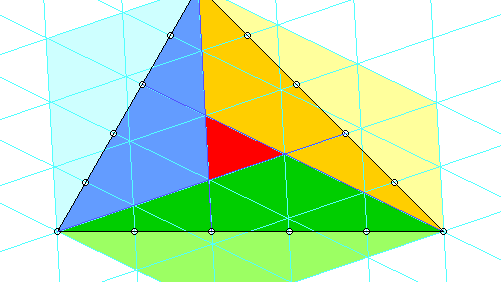
Für einen umwerfend einfachen Beweis zeichnet man drei Parallelenscharen (mit je gleichen Abständen natürlich) derart, dass das innere Dreieck zu einer Zelle darin wird.
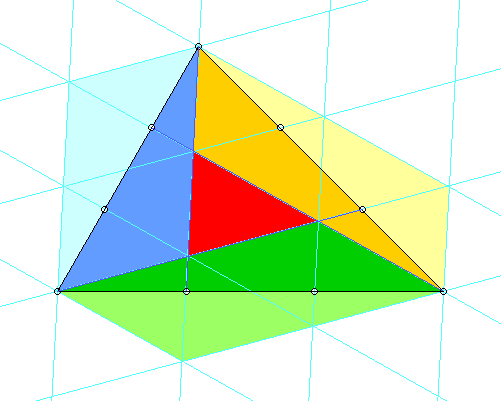
Von den Parallelogrammen, die blau, grün und braun getönt sind, und die je die Fläche von 4 solchen Zellen haben, gehört jeweils die kräftiger getönte Hälfte zum großen Dreieck. Die Fläche des "inneren" verhält sich also zu der des "ganzen" wie 1 : 7.
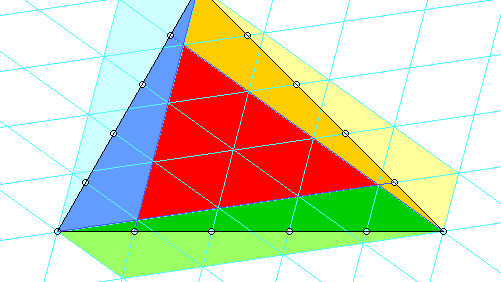
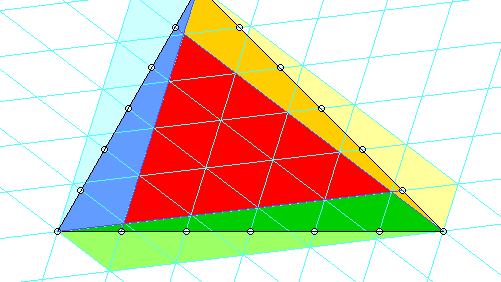
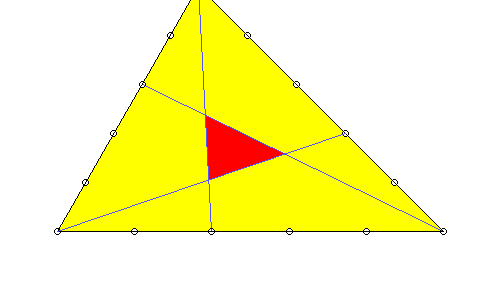
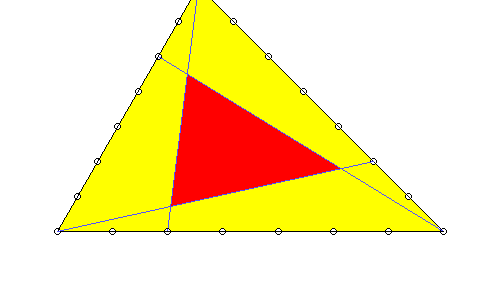
Es sei noch erwähnt, dass es auch für andere Teilungsverhältnisse (die sogar auf den drei Seiten verschieden sein dürfen) Formeln gibt, vgl. Coxeter, Unvergängliche Geometrie, S. 257. Einige folgen in diesen Bildern:







Schreiben Sie uns!
Beitrag schreiben