Hemmes mathematische Rätsel: Das Spinnennetz
Das heutige Rätsel habe ich im Jahr 2009 erdacht.
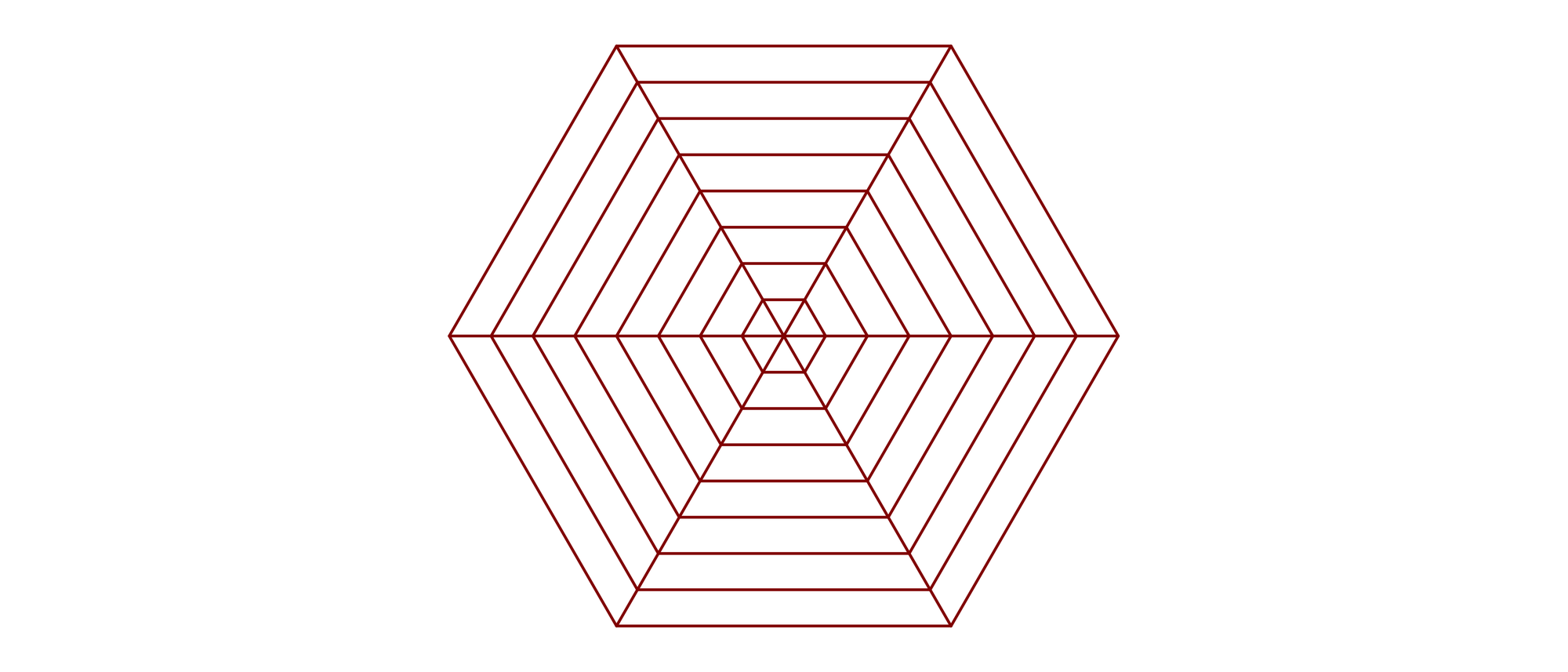
Am Oberlauf des Phlegethons im Regenwald Enigmatiens leben die Spinnen der Gattung Araneus geometricus. An keinem anderen Ort der Welt kommen sie sonst noch vor. Diese Spinnen weben ein Netz, das immer aus acht ineinander verschachtelten regelmäßigen Sechsecken besteht, von denen das äußerste eine Seitenlänge von 13 Zentimetern hat. Benachbarte Sechsecke haben alle voneinander genau den Abstand, den das innerste Sechseck vom Mittelpunkt des Netzes hat. Die Ecken der Sechsecke sind durch sechs Haltefäden mit dem Mittelpunkt des Netzes verbunden, wo Araneus geometricus auf seine Opfer lauert. Wie lang ist der Faden, den die Spinne zum Bau ihres Netzes benötigt?
Das sechseckige Spinnennetz lässt sich in sechs Segmente zerlegen, die jeweils die Form eines gleichseitigen Dreiecks haben und aus acht Netzfäden und einem Haltefaden bestehen.
Die sechs Segmente kann man nun so drehen und umklappen, dass ihren Spitzen abwechselnd nach unten und nach oben zeigen und sich zu einem Parallelogramm zusammenfügen lassen.
Bezeichnet man die Seitenlänge des äußersten Sechsecks des Spinnennetzes mit L, sieht man sofort, dass alle Netzfäden zusammen eine Länge 9 · 3L und alle Haltefäden zusammen 6L haben. Der Faden, den Araneus geometricus zum Bau ihres Netzes benötigt, muss also 27L + 6L = 33L = 429 Zentimeter lang sein.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.